Phép đối xứng tâm

Biểu thức tọa độ của phép đối xứng tâm \(O\left( {0;0} \right)\) là $\left\{ \begin{array}{l}x' =  - x\\y' =  - y\end{array} \right. \Rightarrow M'\left( {2; - 3} \right).$

Từ giả thiết, suy ra \(I\) là trung điểm của \(AA' \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{1 + 1}}{2} = 1\\b = \dfrac{{3 + 7}}{2} = 5\end{array} \right. \Rightarrow T = 6.\)

Ta có phép đổi xứng tâm \(O\) biến điểm \(A\left( {m; - m} \right)\) thành điểm \(A'\left( { - m;m} \right)\).

Do \(A'\) nằm trên đường thẳng \(x - y + 6 = 0\) nên \( - m - m + 6 = 0 \Leftrightarrow m = 3.\)

Dễ thấy các đáp án A, C, D đúng, chỉ có đáp án B sai.

\({D_I}\left( M \right) = M' \Rightarrow I\) là trung điểm của  \(MM' \Rightarrow IM' = IM\) và ba điểm $I,M,M'$ thẳng hàng.

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song với nó.

Dựa vào các đáp án ta thấy chỉ có đường thẳng đáp án D song song với đường thẳng $d$ đã cho vì \(\dfrac{a}{{a'}} = \dfrac{b}{{b'}} = \dfrac{1}{2} \ne \dfrac{4}{{ - 3}}\)

Ta có \(\overrightarrow {IM'}  = \left( {x' - 1;y' - 2} \right),\overrightarrow {IM}  = \left( {x - 1;y - 2} \right).\)

Vì \({D_I}\left( M \right) = M'\)\( \Leftrightarrow \overrightarrow {IM'}  =  - \overrightarrow {IM}  \Leftrightarrow \left\{ \begin{array}{l}x' - 1 =  - \left( {x - 1} \right)\\y' - 2 =  - \left( {y - 2} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' =  - x + 2}\\{y' =  - y + 4}\end{array}.} \right.\)

Vì tam giác đều không có tâm đối xứng

Đường elip có tâm đối xứng là trung điểm của đoạn nối hai tiêu điểm.

Đường tròn có tâm đối xứng là tâm đường tròn.

Đường parabol không có tâm đối xứng.

Hình vuông có tâm đối xứng là giao điểm hai đường chéo.

Tâm đối xứng là các điểm cách đều \(d\) và \(d'\).

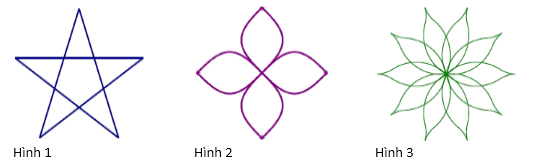
Hình 1: chỉ có trục đối xứng (\(5\) đường thẳng) và không có tâm đối xứng.

Hình 2: Có \(4\) trục đối xứng và có \(1\) tâm đối xứng.

Hình 3: Có \(10\) trục đối xứng và có \(1\) tâm đối xứng.

Đường tròn \(\left( C \right)\) có tâm \(I\left( {3; - 1} \right)\), bán kính \(R = 3.\)

Gọi \(I'\) là điểm đối xứng của \(I\left( {3; - 1} \right)\) qua tâm \(O\left( {0;0} \right)\), suy ra \(I'\left( { - 3;1} \right).\)

Phép đối xứng tâm bảo toàn khoảng cách nên \(R' = R = 3.\)

Vậy đường tròn \(\left( {C'} \right)\) có tâm \(I'\left( { - 3;1} \right).\), bán kính \(R' = 3\) nên \(\left( {C'} \right):{\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = 9.\)

Đường tròn \(\left( C \right)\) có tâm \(K\left( {2;2} \right)\). Đường tròn \(\left( {C'} \right)\) có tâm \(K'\left( {6;4} \right)\).

Tọa độ tâm đối xứng \(I\) là trung điểm của \(KK'\) nên suy ra \(I\left( {4;3} \right)\).

Qua phép đối xứng tâm đường thẳng biến thành đường thẳng song song hoặc trùng với nó nên suy ra \(d':x + y + c = 0.\)

Chọn \(A\left( {1;1} \right)\) thuộc \(d\). Ta có \({N _I}\left( A \right) = A'\left( {x;y} \right) \Leftrightarrow \)\(\left\{ \begin{array}{l}\overrightarrow {IA'}  =  - \overrightarrow {IA} \\A' \in d'\end{array} \right..\)

Từ \(\overrightarrow {IA'}  =  - \overrightarrow {IA}  \Rightarrow A'\left( {1;3} \right)\) thay vào \(d'\) ta được \(1 + 3 + c = 0 \Leftrightarrow c =  - 4\)

\( \Rightarrow d':x + y - 4 = 0\).

Đường thẳng \(\Delta \) có phương trình tổng quát là \(x + 4y - 6 = 0.\)

Biểu thức tọa độ của phép đối xứng tâm \(I\left( {a;b} \right)\) là $\left\{ {\begin{array}{*{20}{c}}{x' = 2a - x}\\{y' = 2b - y}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - 4 - x'}\\{y = 4 - y'}\end{array}} \right..$

Thay vào phương trình đường thẳng \(d\) ta được \(\left( { - 4 - x'} \right) + 4\left( {4 - y'} \right) - 6 = 0\)

\( \Leftrightarrow x' + 4y' - 6 = 0\).

Phép đối xứng tâm \(O\left( {0;0} \right)\) biến điểm \(M\left( {2;1} \right)\) thành điểm \(M'\left( { - 2; - 1} \right).\)

Phép tịnh tiến theo vectơ $\vec v = \left( {1;\,2} \right)$ biến điểm \(M'\) thành điểm \(M''\)

\( \Rightarrow \overrightarrow {M'M''}  = \overrightarrow v  \Rightarrow M''\left( { - 1;1} \right) \equiv D.\)

Nếu phép đối xứng tâm biến $a$ thành $b$ thì tâm đối xứng nằm trên đường thẳng song song và cách đều $a$ và $b$.

Đường thẳng song song và cách đều $a$ và $b$ có phương trình là \(3x + 4y + 2 = 0\)

Lấy điểm \(M\left( {3 - 2m;m} \right)\) thuộc \(\Delta .\)

Gọi \(N\) là ảnh của \(M\) qua phép đối xứng tâm \(I\left( {1; - 3} \right) \Rightarrow N\left( {2m - 1; - 6 - m} \right).\)

Vì \(N \in \Delta '\) nên \(\left( {2m - 1} \right) - 2\left( { - 6 - m} \right) - 7 = 0 \Leftrightarrow m =  - 1.\)

Với \(m =  - 1\) \( \Rightarrow M\left( {5; - 1} \right),{\rm{ }}N\left( { - 3; - 5} \right)\) \( \Rightarrow MN = 4\sqrt 5 \)

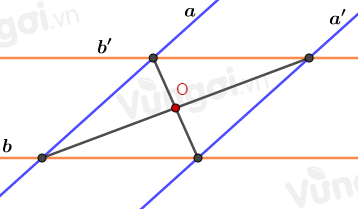
Đó là phép đối xứng qua tâm hình bình hành tạo thành bởi bốn đường thẳng đã cho.

Đáp án A: Hàm số \(y = f\left( x \right) = 2{x^2}\) làm hàm số chẵn trên \(\mathbb{R}\) vì \(f\left( { - x} \right) = 2{\left( { - x} \right)^2} = 2{x^2} = f\left( x \right)\).

Đáp án B: Hàm số \(y = f\left( x \right) = {x^3}\) là hàm số lẻ trên \(\mathbb{R}\) vì \(f\left( { - x} \right) = {\left( { - x} \right)^3} =  - {x^3} =  - f\left( x \right)\).

Đáp án C: Hàm số \(y = f\left( x \right) = {x^3}\tan x\) là hàm số chẵn trên \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi } \right\}\) vì :

\(f\left( { - x} \right) = {\left( { - x} \right)^3}\tan \left( { - x} \right)\) \( =  - {x^3}.\left( { - \tan x} \right) = {x^3}\tan x = f\left( x \right)\).

Đáp án D : Hàm số \(y = f\left( x \right) = \cos x\) là hàm số chẵn trên \(\mathbb{R}\) vì \(f\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = f\left( x \right)\).

Vậy chỉ có đồ thị hàm số \(y = {x^3}\) nhận \(O\) làm tâm đối xứng.

Biểu thức tọa độ của phép đối xứng tâm \(I\left( {a;b} \right)\) là $\left\{ \begin{array}{l}x' = 2a - x = 2 - x\\y' = 2b - y =  - y\end{array} \right.$

$ \Rightarrow \left\{ \begin{array}{l}x = 2 - x'\\y =  - y'\end{array} \right.$. Thay vào \(\left( P \right)\) ta được \({\left( { - y'} \right)^2} = 2 - x' \Leftrightarrow {\left( {y'} \right)^2} =  - x' + 2.\)