Cho lăng trụ đứng \(ABC.A'B'C'\). Mệnh đề nào sau đây sai?
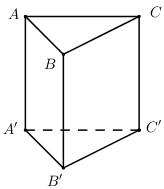
Ta có : \(\left( {ABC} \right)//\left( {A'B'C'} \right)\)
\( \Rightarrow d\left( {\left( {ABC} \right);\left( {A'B'C'} \right)} \right) = d\left( {B;\left( {A'B'C'} \right)} \right) = BB'\,\left( {Do\,\,BB' \bot \left( {A'B'C'} \right)} \right)\), suy ra đáp án A đúng.
Vì \(ABC.A'B'C'\) là lăng trụ đứng nên các mặt bên của hình lăng trụ \(ABC.A'B'C'\) là các hình chữ nhật, suy ra đáp án B đúng.
Ta có:
\(\begin{array}{l}BB'//AA' \subset \left( {ACC'A'} \right) \Rightarrow BB'//\left( {ACC'A'} \right)\\ \Rightarrow d\left( {B;\left( {ACC'A'} \right)} \right) = d\left( {B';\left( {ACC'A'} \right)} \right)\end{array}\)
Suy ra đáp án C đúng.
Cho hình hộp $ABCD.A'B'C'D'$. Khẳng định nào sau đây sai?
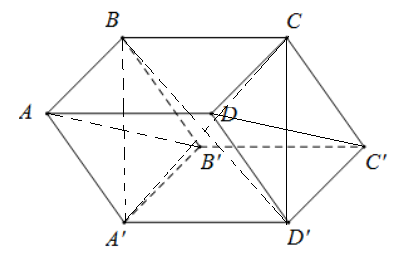
Từ hình vẽ ta thấy \(DC'//AB'\) nên đáp án D sai.
Cho hình hộp $ABCD.A'B'C'D'$. Mặt phẳng $\left( {AB'D'} \right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?
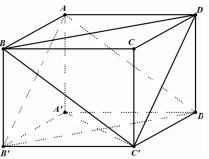
Do \(ADC'B'\) là hình bình hành nên \(AB'//DC'\).
Do \(ABC'D'\) là hình bình hành nên \(AD'//BC'\).
Mà \(AB',AD' \subset \left( {AB'D'} \right);BC',DC' \subset \left( {BC'D} \right)\) nên \(\left( {AB'D'} \right)//\left( {BC'D} \right)\).
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là trung điểm của \(AB\), mặt phẳng \(\left( {MA'C'} \right)\) cắt hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là trung điểm của \(AB\), mặt phẳng \(\left( {MA'C'} \right)\) cắt hình hộp \(ABCD.A'B'C'D'\) theo thiết diện là hình gì?
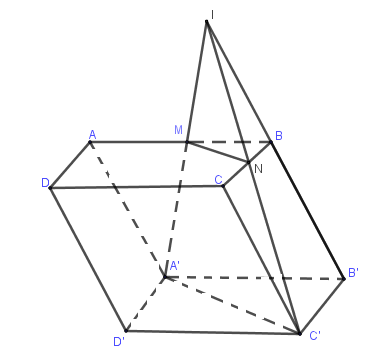
Trong mặt phẳng \(\left( {ABB'A'} \right),A'M\) cắt \(B'B\) tại \(I\).
Trong mặt phẳng \(\left( {BCC'B'} \right),IC'\) cắt \(BC\) tại \(N\).
Tứ giác \(A'MNC'\) là thiết diện cần tìm.
Ta có: \(MB//A'B' \Rightarrow \dfrac{{MB}}{{A'B'}} = \dfrac{{IB}}{{IB'}} = \dfrac{{IM}}{{IA'}} = \dfrac{1}{2} \Rightarrow M\) là trung điểm \(IA'\).
Mà \(BN//B'C' \Rightarrow \dfrac{{IB}}{{IB'}} = \dfrac{{IN}}{{IC'}} = \dfrac{1}{2} \Rightarrow N\) là trung điểm \(IC'\).
Do đó \(MN\) là đường trung bình của tam giác \(IA'C' \Rightarrow MN//A'C' \Rightarrow MNC'A'\) là hình thang.
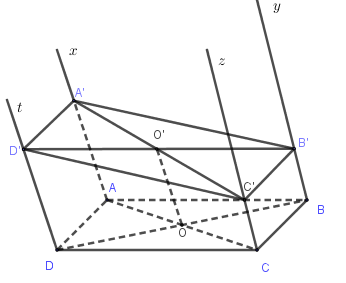
Cho hình bình hành \(ABCD\). Vẽ các tia \(Ax,By,Cz,Dt\) song song, cùng hướng nhau và không nằm trong \(mp\left( {ABCD} \right)\). Mặt phẳng \(\left( \alpha \right)\) cắt \(Ax,By,Cz,Dt\) lần lượt tại \(A',B',C',D'\), gọi \(O,O'\) lần lượt là tâm hình bình hành và giao điểm của hai đường thẳng \(A'C'\) với \(B'D'\). Khẳng định nào sau đây sai?
Ta có: \(AB//CD,AA'//DD'\) và \(AA',AB \subset \left( {ABB'A'} \right);CD,DD' \subset \left( {CDD'C'} \right)\)
Do đó \(mp\left( {AA'B'B} \right)//mp\left( {DD'C'C} \right)\), đáp án B đúng.
Mặt khác,
\(\left. \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {ABB'A'} \right) = A'B'\\\left( {A'B'C'D'} \right) \cap \left( {DCC'D'} \right) = C'D'\\\left( {ABB'A'} \right)//\left( {DCC'D'} \right)\end{array} \right\} \Rightarrow A'B'//C'D'\)
\(\left. \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {ADD'A'} \right) = A'D'\\\left( {A'B'C'D'} \right) \cap \left( {BCC'B'} \right) = C'B'\\\left( {ADD'A'} \right)//\left( {BCC'B'} \right)\end{array} \right\} \Rightarrow A'D'//C'B'\)
Do đó, tứ giác \(A'B'C'D'\) là hình bình hành nên đáp án A đúng.
Do \(O,O'\) lần lượt là tâm các hình bình hành nên \(O,O'\) lần lượt là trung điểm của \(AC,A'C'\) nên \(OO'\) là đường trung bình trong hình thang \(AA'C'C\).
Do đó \(OO'//AA'\) nên D đúng.
Số mặt chéo của hình hộp \(ABCD.A'B'C'D'\) là:
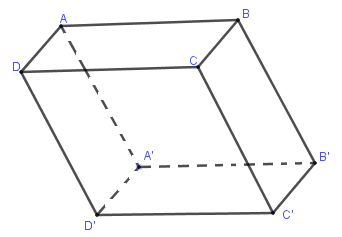
Các mặt chéo của hình hộp là: \(\left( {ADC'B'} \right),\left( {A'D'CB} \right),\left( {ABC'D'} \right),\left( {DCB'A'} \right),\left( {ACC'A'} \right),\left( {BDD'B'} \right)\).
Cho hình hộp \(ABCD.A'B'C'D'\), mặt phẳng \(\left( \alpha \right)\) qua \(AB\) và trung điểm \(M\) của \(CC'\) thì cắt hình hộp theo thiết diện là hình gì?
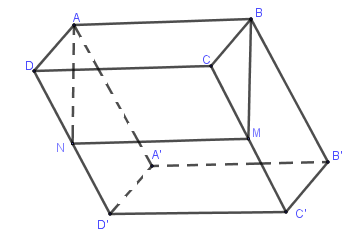
Ta sử dụng tính chất: Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó sẽ cắt mặt phẳng còn lại và giao tuyến của chúng song song.
Ta có:
\(\left. \begin{array}{l}\left( {ADD'A'} \right)//\left( {BCC'B'} \right)\\\left( {ABM} \right) \cap \left( {BCC'B'} \right) = BM\end{array} \right\} \Rightarrow \left( {ABM} \right) \cap \left( {ADD'A'} \right) = AN//BM\) với \(N \in DD'\).
Do đó tứ giác \(ABMN\) là hình thang.
Lại có:
\(\left. \begin{array}{l}\left( {ABB'A'} \right)//\left( {DCC'D'} \right)\\\left( {ABMN} \right) \cap \left( {ABB'A'} \right) = AB\\\left( {ABMN} \right) \cap \left( {DCC'D'} \right) = MN\end{array} \right\} \Rightarrow AB//MN\)
Do đó tứ giác \(ABMN\) là hình bình hành.
Cho hình hộp \(ABCD.A'B'C'D\). Gọi \(O,O'\) lần lượt là tâm các hình bình hành \(ABB'A',DCC'D'\). Khẳng định nào sau đây sai?
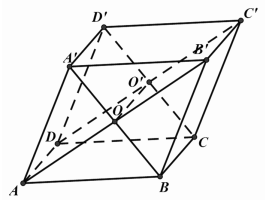
\(ADC'B'\) là hình bình hành có \(OO'\) là đường trung bình nên \(\overrightarrow {OO'} = \overrightarrow {AD} \) và đáp án A, D đúng.
Mà \(OO'//AD\) nên \(OO'//\left( {ADD'A'} \right)\) nên B đúng.
Ngoài ra \(OO'\) và \(BB'\) chéo nhau nên C sai.
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I\) là trung điểm của \(AB\). Mặt phẳng \(\left( {IB'D'} \right)\) cắt hình hộp theo thiết diện là hình gì?
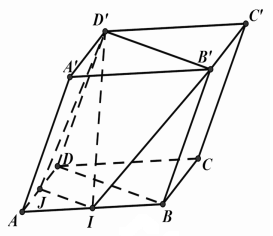
Ta có:
\(\left. \begin{array}{l}\left( {IB'D'} \right) \cap \left( {A'B'C'D'} \right) = B'D'\\\left( {A'B'C'D'} \right)//\left( {ABCD} \right)\end{array} \right\} \Rightarrow \left( {IB'D'} \right) \cap \left( {ABCD} \right) = JI//B'D'\) với \(J \in AD\)
Mà \(BD//B'D'\) nên \(JI//BD \Rightarrow J\) là trung điểm của \(AD\).
Vậy thiết diện là hình thang \(JIB'D'\).
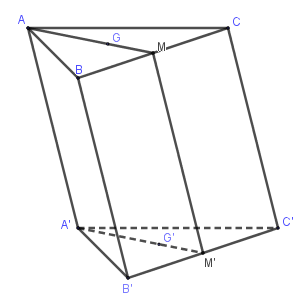
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\), \(G,G'\) lần lượt là trọng tâm của các tam giác \(\Delta ABC,\Delta A'B'C'\). Bốn điểm nào sau đây đồng phẳng?
Vì \(M,M'\) là trung điểm của \(BC,B'C'\) nên \(MM'//BB'//CC'//AA'\) và \(MM' = BB' = CC' = AA'\).
Do đó \(A'M'MA\) là hình bình hành nên bốn điểm \(A,A',M,M'\) đồng phẳng.
Ngoài ra \(G' \in A'M',G \in AM\) nên hai điểm \(G,G'\) cũng thuộc mặt phẳng \(\left( {AMM'A'} \right)\).
Nên bốn điểm \(A,G',M',G\) đồng phẳng.
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,N\) lần lượt là trung điểm của \(BB',CC'\) và đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {A'B'C'} \right)\). Khẳng định nào sau đây đúng?
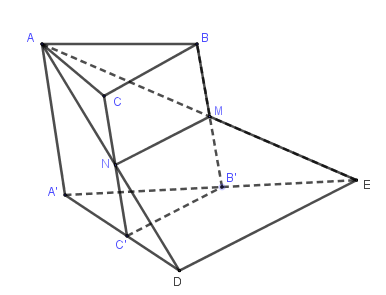
Gọi \(D = AN \cap A'C' \Rightarrow D \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\) và \(E = AM \cap A'B' \Rightarrow E \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\).
Khi đó \(DE = \left( {AMN} \right) \cap \left( {A'B'C'} \right) = \Delta \).
Lại có: \(\left\{ \begin{array}{l}\left( {AMN} \right) \cap \left( {MNC'B'} \right) = MN\\\left( {A'B'C'} \right) \cap \left( {MNC'B'} \right) = B'C'\\\left( {AMN} \right) \cap \left( {A'B'C'} \right) = DE\\MN//B'C'\end{array} \right. \Rightarrow MN//B'C'//DE\) (định lý ba giao tuyến)
Do đó \(DE//B'C'//BC\).
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(H\) là trung điểm của \(A'B'\). Đường thẳng \(B'C\) song song với mặt phẳng nào sau đây?
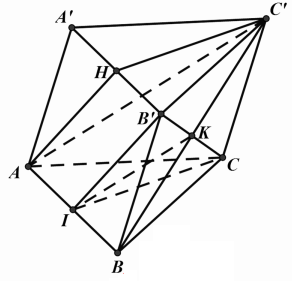
Gọi \(K = BC' \cap B'C\) và \(I\) là trung điểm của \(AB\).
Khi đó \(AHB'I\) là hình bình hành \(\left( {AI//HB',AI = HB'} \right)\).
Suy ra \(AH//B'I\).
Mặt khác, xét tam giác \(ABC'\) có \(IK\) là đường trung bình của tam giác nên \(IK//AC'\).
Do đó \(\left\{ \begin{array}{l}IB'//AH\\IK//AC'\\IB',IK \subset \left( {IB'C} \right)\\AH,AC' \subset \left( {AHC'} \right)\end{array} \right. \Rightarrow \left( {IB'C} \right)//\left( {AHC'} \right) \Rightarrow B'C//\left( {AHC'} \right)\)
Cho hình hộp $ABCD.A'B'C'D'$ có các cạnh bên $AA',BB',CC',DD'$ . Khẳng định nào dưới đây là sai?
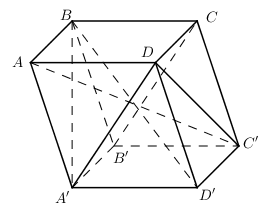
Ta có: \(\left\{ \begin{array}{l}AA'//DD'\\AB//CD\end{array} \right. \Rightarrow \left( {AA'B'B} \right)//\left( {DD'C'C} \right) \Rightarrow A\) đúng.
Có: $A’B’ // CD$ và $A’B’ = CD$ nên $A’B’CD$ là hình bình hành, do đó C đúng.
B sai vì \(I = AC' \cap BD' \Rightarrow I \in \left( {BA'D'} \right) \cap \left( {ADC'} \right)\) nên hai mặt phẳng không song song.
D đương nhiên đúng.
Cho hình hộp \(ABCD.A'B'C'D'\). Cắt hình hộp bởi mặt phẳng chứa một cạnh của hình hộp ta được thiết diện là tứ giác \(\left( T \right)\). Chọn khẳng định đúng :
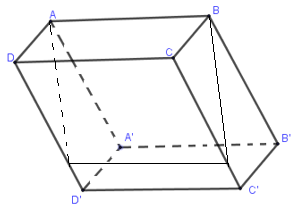
Thiết diện tạo thành là hình bình hành.
Nhận xét nào sau đây không đúng về hình chóp cụt?
Các mặt bên của hình chóp cụt chỉ là những hình thang chứ không phải hình thang cân.
Trong các hình sau, hình nào là hình hộp?
Hình thoi cũng là một hình bình hành nên hình lăng trụ có đáy là hình thoi cũng là một hình hộp
Phát biểu nào “không” đúng về hình hộp?
Hai đỉnh của hình hộp được gọi là đối diện nếu chúng không cùng nằm trên một mặt nào của hình hộp. Vậy chỉ có 4 cặp đỉnh đối diện trong hình hộp.
Cho các mệnh đề:
(1) Hình hộp là một hình lăng trụ.
(2) Hình lăng trụ có tất cả các cạnh song song.
(3) Hình lăng trụ có tất cả các mặt bên bằng nhau.
(4) Hình lăng trụ có các mặt bên là hình bình hành.
(5) Hình hộp có các mặt đối diện bằng nhau.
Các phát biểu đúng là:
Hai cạnh kề bất kỳ của hình lăng trụ không song song với nhau.
Các mặt bên của hình lăng trụ là các hình bình hành có thể không bằng nhau.
Vậy các khẳng định đúng là (1), (4), (5).

