Trong hệ trục tọa độ \(Oxy\), cho \(\overrightarrow v \left( {3;3} \right)\) và đường tròn \(\left( C \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\). Tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép tịnh tiến \({T_{\overrightarrow v }}.\)
Bước 1:
Đường tròn (C): \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\)có tâm I(1;-2); bán kinh R=3.
Bước 2:
Gọi I’ là tâm đường tròn (C’).
Phép tịnh tiến điểm I thành điểm I’ theo véc-tơ \(\overrightarrow v \left( {3;3} \right)\)thì \(\overrightarrow {II'} = \overrightarrow v \)
Suy ra \(I'\left( {4;1} \right)\)
Bước 3:
Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính nên:
Đường tròn (C’) có tâm là \(I'\left( {4;1} \right)\); R=3.
Vậy (C’):\({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
Trong mặt phẳng với hệ tọa độ Oxy. Phép dời hình \(\left\{ \begin{array}{l}x' = x - 3\\y' = y + 1\end{array} \right.\) biến parabol \(\left( P \right):\,\,y = {x^2} + 1\) thành parabol \(\left( {P'} \right)\) có phương trình là:
Gọi \(M\left( {x;y} \right) \in \left( P \right)\) và \(M'\left( {x';y'} \right) = F\left( M \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' = x - 3\\y' = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 3\\y = y' - 1\end{array} \right.\).
\( \Rightarrow M\left( {x' + 3;y' - 1} \right)\).
Vì \(M \in \left( P \right) \Rightarrow y' - 1 = {\left( {x' + 3} \right)^2} + 1\)
\(\begin{array}{l} \Leftrightarrow y' = x{'^2} + 6x' + 9 + 1 + 1\\ \Leftrightarrow y' = x{'^2} + 6x' + 11\end{array}\)
Do đó điểm \(M'\) thuộc \(\left( {P'} \right):\,\,y = {x^2} + 6x + 11\).
Vậy phép dời hình đã cho biến \(\left( P \right):\,\,y = {x^2} + 1\) thành \(\left( {P'} \right):\,\,y = {x^2} + 6x + 11\).
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + 2y – 1 = 0 và vectơ \(\overrightarrow v \left( {2;m} \right)\). Để phép tịnh tiến theo \(\overrightarrow v \) biến đường thẳng d thành chính nó, ta phải chọn m là số:
Để phép tịnh tiến theo \(\overrightarrow v \) biến đường thẳng d thành chính nó thì \(\overrightarrow v \left( {2;m} \right)\) phải cùng phương với đường thẳng d.
Đường thẳng d có 1 VTCP là \(\overrightarrow u \left( {2; - 1} \right)\), do đó \(\overrightarrow v \left( {2;m} \right)\) và \(\overrightarrow u \left( {2; - 1} \right)\) cùng phương.
Vậy \(m = - 1\).
Cho hình vuông \(ABCD\) tâm \(I\). Gọi \(M,N\) lần lượt là trung điểm của \(AD,DC.\) Phép tịnh tiến theo vecto nào sau đây biến \(\Delta AMI\) thành \(\Delta MDN?\)
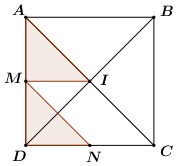
Ta có: \(IN\) là đường trung bình của tam giác \(ACD \Rightarrow IN = \dfrac{1}{2}AD = AM\).
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {IN} \Rightarrow {T_{\overrightarrow {AM} }}\left( I \right) = N\).
Dễ thấy \(\overrightarrow {AM} = \overrightarrow {MD} \Rightarrow {T_{\overrightarrow {AM} }}\left( M \right) = D\) và hiển nhiên \({T_{\overrightarrow {AM} }}\left( A \right) = M\).
Vậy \({T_{\overrightarrow {AM} }}\left( {\Delta AMI} \right) = \Delta MDN\).
Trong mặt phẳng tọa độ \(Oxy\), cho \(\Delta :\,\,x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là:
Vì \(\Delta = {T_{\overrightarrow u }}\left( d \right) \Rightarrow \Delta \parallel d \Rightarrow \) Phương trình \(\Delta \) có dạng: \(x - 2y + c = 0\,\,\left( \Delta \right)\).
Lấy \(A\left( {1;0} \right)\) bất kì thuộc \(d\). Gọi \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow A' \in \Delta \).
Ta có: \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_A} + {x_{\overrightarrow u }} = 1 + 4 = 5\\{y_{A'}} = {y_A} + {y_{\overrightarrow u }} = 0 + 3 = 3\end{array} \right. \Rightarrow A'\left( {5;3} \right)\).
Vì \(A' \in \Delta \Rightarrow 5 - 2.3 + c = 0 \Leftrightarrow c = 1\).
Vậy phương trình đường thẳng \(\Delta \) là: \(x - 2y + 1 = 0\).
Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta :\,2x - 3y - 5 = 0\). Ảnh của đường \(\Delta \) qua phép tịnh tiến theo vectơ \(\overrightarrow u = \left( { - 1;2} \right)\) là đường thẳng nào?
Gọi \(M\left( {x;y} \right) \in \Delta ;{T_{\overrightarrow u }}\left( M \right) = M'\left( {x';y'} \right) \in \Delta '\)
\( \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right. \Rightarrow M\left( {x' + 1;y' - 2} \right) \in d\)
\(M \in d \Rightarrow 2\left( {x' + 1} \right) - 3\left( {y' - 2} \right) - 5 = 0 \Leftrightarrow 2x' - 3y' + 3 = 0\)
Vậy phương trình ảnh của đường thẳng \(\Delta \) là: \(\Delta ' = 2x - 3y + 3 = 0\).
Trong mặt phẳng tọa độ \(Oxy\), viết phương trình đường thẳng \(\Delta '\) là ảnh của đường thẳng \(\Delta :x + 2y - 1 = 0\) qua phép tịnh tiến theo véctơ \(\overrightarrow v = \left( {1; - 1} \right)\).
Bước 1:
Vì \(\Delta '\parallel \Delta \) nên phương trình \(\Delta '\) có dạng \(\Delta ':x + 2y + c = 0\).
Bước 2:
Lấy \(A\left( {1;0} \right) \in \Delta \), khi đó \({T_{\overrightarrow v }}\left( A \right) = A' \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 1 = 2\\{y_{A'}} = 0 - 1 = - 1\end{array} \right. \Rightarrow A'\left( {2; - 1} \right)\).
Bước 3:
\(A' \in \Delta ' \Leftrightarrow 2 + 2.\left( { - 1} \right) + c = 0 \Leftrightarrow c = 0\).
Bước 4:
Vậy phương trình \(\Delta ':x + 2y = 0\).
Trong mặt phẳng tọa độ \(Oxy\) cho véctơ \(\vec v = \left( {a;b} \right).\) Giả sử phép tịnh tiến theo \(\vec v\) biến điểm \(M\left( {x;y} \right)\) thành \(M'\left( {x';y'} \right)\). Ta có biểu thức tọa độ của phép tịnh tiến theo vectơ \(\vec v\) là:
Ta có \(\overrightarrow {MM'} = \left( {x' - x;y' - y} \right)\).
Theo giả thiết \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow v \) \( \Rightarrow \left\{ \begin{array}{l}x' - x = a\\y' - y = b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\) cho phép biến hình \(f\) xác định như sau: Với mỗi \(M\left( {x;y} \right),\) ta có \(M' = f\left( M \right)\) sao cho \(M'\left( {x';y'} \right)\) thỏa mãn \(x' = x + 2;\)\(y' = y - 3.\) Mệnh đề nào sau đây là đúng?
Theo giả thiết, ta có \(\left\{ \begin{array}{l}x' = x + 2\\y' = y - 3\end{array} \right. \Rightarrow \overrightarrow v = \left( {2; - 3} \right).\)
Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm $M\left( { - 10;1} \right)$ và $M'\left( {3;8} \right).$ Phép tịnh tiến theo vectơ $\vec v$ biến điểm \(M\) thành \(M'\). Mệnh đề nào sau đây là đúng?
Gọi $\vec v = \left( {a;b} \right)$.
Theo giả thiết: ${T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \vec v$ $ \Rightarrow \left\{ \begin{array}{l}3 - \left( { - 10} \right) = a\\8 - 1 = b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 13\\b = 7\end{array} \right.$
Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?
Có đúng một phép tịnh tiến. Tịnh tiến theo vectơ–không.
Cho hai đoạn thẳng $AB$ và$\;A'B'$. Điều kiện cần và đủ để có thể tịnh tiến biến $A$ thành $A'$ và biến $B$ thành $B'$ là
Giả sử có phép tịnh tiến \({T_{\overrightarrow v }}\) biến $A$ thành $A'$ và biến $B$ thành $B'$.
Khi đó ta có \(\left\{ \begin{array}{l}{T_{\overrightarrow v }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'} = \vec v\\{T_{\overrightarrow v }}\left( B \right) = B' \Leftrightarrow \overrightarrow {BB'} = \vec v\end{array} \right. \Rightarrow \overrightarrow {AA'} = \overrightarrow {BB'} \)
\( \Rightarrow \overrightarrow {AB} + \overrightarrow {BA'} = \overrightarrow {BA'} + \overrightarrow {A'B'} \) \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {A'B'} \)
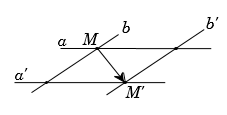
Cho bốn đường thẳng \(a,{\rm{ }}b,{\rm{ }}a',{\rm{ }}b'\) trong đó $a\parallel a'$, \(b\parallel b'\) và \(a\) cắt \(b\). Có bao nhiêu phép tịnh tiến biến \(a\) thành \(a'\) và \(b\) thành \(b'\)?
Giả sử \(a\) cắt \(b\) tại \(M;\) \(a'\) cắt \(b'\) tại \(M'.\)
Khi đó vectơ \(\overrightarrow {MM'} \) là vectơ tịnh tiến thỏa mãn yêu cầu bài toán.
Cho hình bình hành$ABCD$. Phép tịnh tiến theo vectơ nào dưới đây biến đường thẳng $AB$ thành đường thẳng $CD$ và biến đường thẳng $AD$ thành đường thẳng $BC$?

Vectơ tịnh tiến \(\overrightarrow {AC} \) biến đường thẳng AB thành CD và biến AD thành BC. Chọn B.
Cho hình bình hành $ABCD$, $M$là một điểm thay đổi trên cạnh $AB$. Phép tịnh tiến theo vectơ $\overrightarrow {BC} $ biến điểm $M$ thành $M'$. Mệnh nào sau đây đúng?
Ta có ${T_{\overrightarrow {BC} }}\left( M \right) = M'$ $ \Leftrightarrow \overrightarrow {MM'} = \overrightarrow {BC} \Rightarrow M' \in CD$.
Trong mặt phẳng tọa độ \(Oxy\) cho điểm \(A\left( {2;5} \right).\) Phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {1;2} \right)\) biến \(A\) thành điểm \(A'\) có tọa độ là:
Bước 1:
Gọi \(A'\left( {x;y} \right) \Rightarrow \overrightarrow {AA'} = \left( {x - 2;y - 5} \right).\)
Bước 2:
Ta có \({T_{\overrightarrow v }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'} = \overrightarrow v \) \( \Rightarrow \left\{ \begin{array}{l}x - 2 = 1\\y - 5 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 7\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\) cho vectơ \(\overrightarrow v = \left( { - 3;2} \right)\) và điểm \(A\left( {1;3} \right)\). Ảnh của điểm \(A\) qua phép tịnh tiến theo vectơ \(\overrightarrow v \) là điểm có tọa độ nào trong các tọa độ sau?
Gọi \(A'\left( {x;y} \right)\) là ảnh của \(A\) qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( { - 3;2} \right)\)
\( \Rightarrow \overrightarrow {AA'} = \left( {x - 1;y - 3} \right).\)
Ta có ${T_{\overrightarrow v }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'} = \vec v$ $ \Rightarrow \left\{ \begin{array}{l}x - 1 = - 3\\y - 3 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 5\end{array} \right.$
Trong mặt phẳng tọa độ \(Oxy\) nếu phép tịnh tiến biến điểm $A\left( {2; - 1} \right)$ thành điểm $A'\left( {2018;2015} \right)$ thì nó biến đường thẳng nào sau đây thành chính nó?
Gọi \(\vec v\) là vectơ thỏa mãn \({T_{\vec v}}\left( A \right) = A'\)\( \Rightarrow \vec v = \overrightarrow {AA'} = \left( {2016;2016} \right)\)
Đường thẳng biến thành chính nó khi nó có vectơ chỉ phương cùng phương với \(\vec v.\)
Xét đáp án B. Đường thẳng có phương trình $x - y - 100 = 0$ có vectơ pháp tuyến \(\vec n = \left( {1; - 1} \right)\), suy ra vectơ chỉ phương \(\vec u = \left( {1;1} \right)\parallel \vec v\) (thỏa mãn).
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(d\) có phương trình \(2x - y + 1 = 0\). Để phép tịnh tiến theo vectơ \(\vec v\) biến \(d\) thành chính nó thì \(\vec v\) phải là vectơ nào trong các vectơ sau?
Bước 1:
Đường thẳng \(d\) có VTPT \(\vec n = \left( {2; - 1} \right)\) \( \Rightarrow \) VTCP \(\vec u = \left( {1;2} \right)\).
Bước 2:
Để \(d\) biến thành chính nó khi và chỉ khi vectơ \(\overrightarrow v \) cùng phương với vectơ chỉ phương của \(d.\)
Vậy \(\vec v = \left( {1;2} \right).\)
Trong mặt phẳng tọa độ \(Oxy\) cho hai đường thẳng song song \(a\) và \(b\) lần lượt có phương trình \(2x - y + 4 = 0\) và \(2x - y - 1 = 0\). Tìm giá trị thực của tham số \(m\) để phép tịnh tiến \(T\) theo vectơ \(\vec u = \left( {m; - 3} \right)\) biến đường thẳng \(a\) thành đường thẳng \(b\).
Chọn \(A\left( {0;4} \right) \in d\).
Ta có \({T_{\overrightarrow u }}\left( A \right) = A'\left( {x;y} \right) \Rightarrow \left\{ \begin{array}{l}x = 0 + m\\y = 4 + \left( { - 3} \right)\end{array} \right. \Rightarrow A'\left( {m;1} \right).\)
Vì \({T_{\overrightarrow u }}\) biến \(a\) thành \(b\) nên \(A' \in b \Leftrightarrow 2m - 1 - 1 = 0 \Leftrightarrow m = 1.\)

