Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau (hình vẽ minh họa).
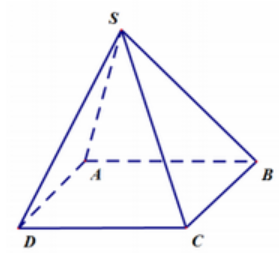
Số đo góc giữa hai đường thẳng SA và CD bằng
Bước 1:
\(CD||AB \Rightarrow \widehat {\left( {SA,CD} \right)}\)\( = \widehat {\left( {SA,AB} \right)} = \widehat {SAB}\)
Bước 2:
Vì S.ABCD có tất cả các cạnh bằng nhau nên tam giác SAB là tam giác đều.
\( \Rightarrow \widehat {SAB} = 60^\circ \)
Đề thi THPT QG - 2021 - mã 103
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \(A'B\) và \(CC'\) bằng:
+ Do \(CC'//BB' \Rightarrow \angle \left( {A'B;CC'} \right) = \angle \left( {A'B;BB'} \right) = \angle A'BB'\).
+ Xét \(\Delta A'BB'\) vuông tại \(B\) có: \(BB' = A'B'\).
\( \Rightarrow \Delta B'BC\) vuông cân tại \(B \Rightarrow \angle A'BB' = {45^0}\).
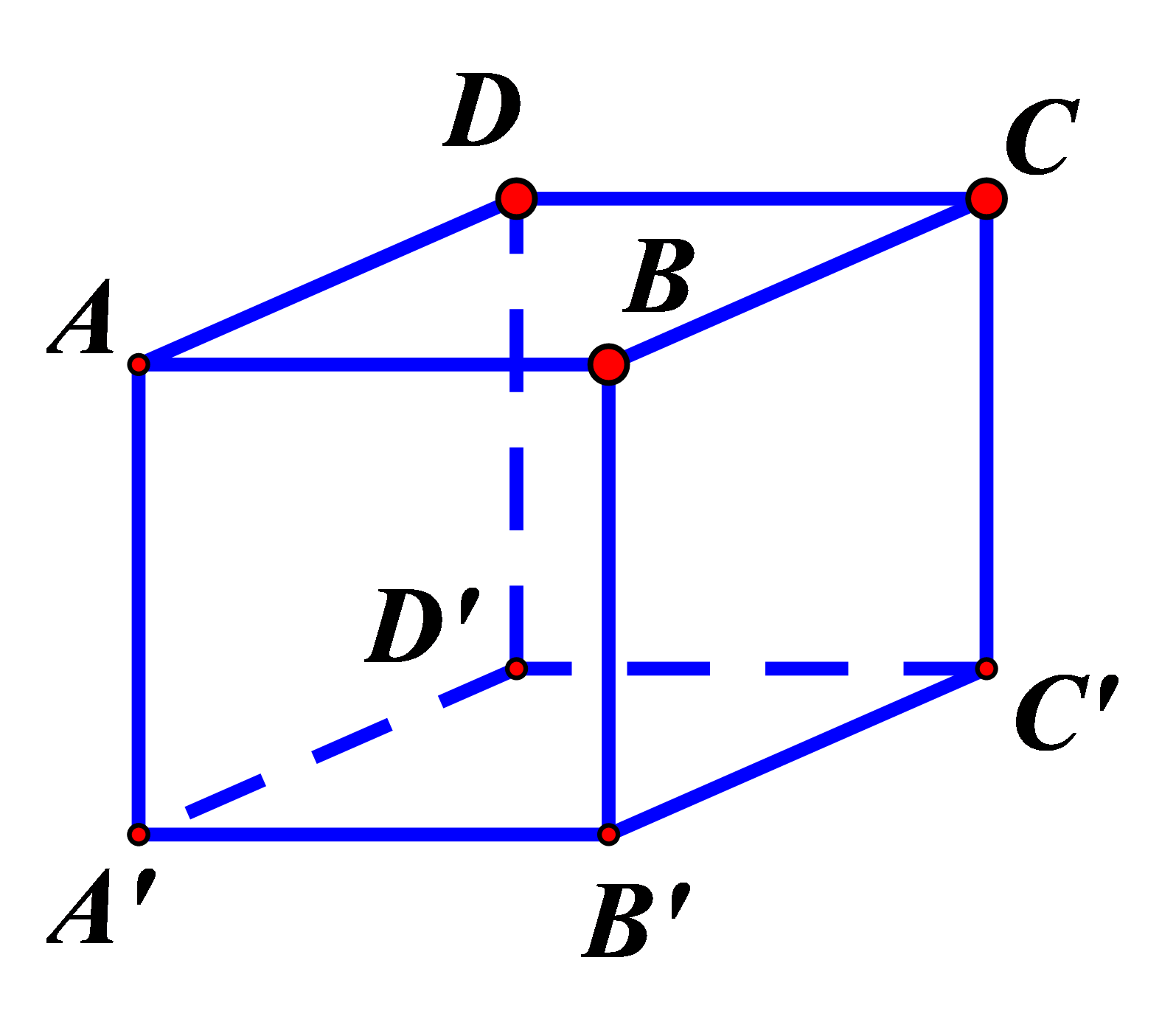
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \({A^\prime }{C^\prime }\) và BD bằng
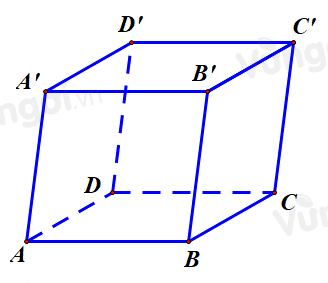
\({A^\prime }{C^\prime }\) song song AC nên góc giữa hai đường thẳng \({A^\prime }{C^\prime }\) và BD bằng góc giữa AC và BD và bằng \({90^0 }\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \(AB'\) và \(CC'\) bằng
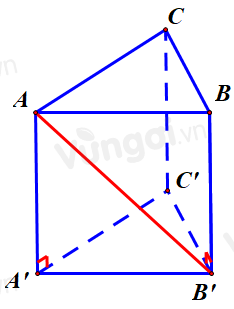
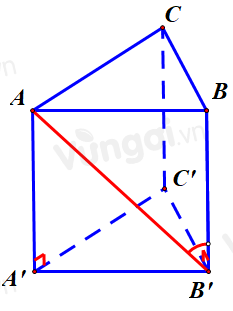
Ta có: \(BB'//CC' \Rightarrow \angle \left( {AB',CC'} \right) = \angle \left( {AB',B'B} \right) = \angle AB'B\)
Mà \(ABC.A'B'C'\) là hình lăng trụ đứng có tất cả các cạnh bằng nhau nên mặt bên là hình vuông \( \Rightarrow \angle AB'B = {45^o}\)
Đề thi THPT QG - 2021 - mã 101
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \(AA'\) và \(BC'\) bằng
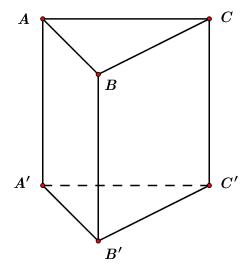
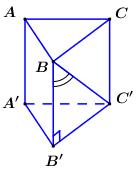
Bước 1:
Do \(AA'//BB' \Rightarrow \angle \left( {AA';BC'} \right) \)\(= d\left( {BB';BC'} \right) = \angle B'BC\).
Bước 2:
Xét \(\Delta B'BC\) vuông tại \(B'\) có: \(BB' = B'C' = a\).
\( \Rightarrow \Delta B'BC\) vuông cân tại \(B' \Rightarrow \angle B'BC = {45^0}\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(BA'\) và \(CD\) bằng
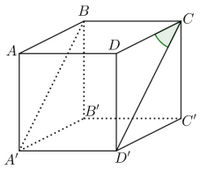
Bước 1:
\(CD'||A'B \Rightarrow \widehat {\left( {BA',CD} \right)}\)\( = \widehat {\left( {CD',CD} \right)} = \widehat {DCD'}\)
Bước 2:
Vì tam giác $DCD'$ là tam giác vuông cân.
\( \Rightarrow \widehat {DCD'} = 45^\circ \)
Vậy góc giữa BA' và CD là \({45^0}\)
Đề thi THPT QG - 2021 - mã 102
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \({\rm{AA}}'\) và \(B'C\) bằng
Ta có \(AA'//BB'\) nên \(\angle \left( {AA',B'C} \right) = \angle \left( {BB',B'C} \right) = \angle BB'C\)
Do \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau nên tứ giác \(BB'C'C\) là hình vuông \( \Rightarrow \angle BB'C = {45^o}\)
Trong các mệnh đề dưới đây mệnh đề đúng là?
Đáp án B sai vì vẫn có thể xảy ra các trường hợp hai đường thẳng đó chéo nhau, cắt nhau, trùng nhau hoặc thậm chí là vuông góc.
Do đó đáp án D cũng sai.
Đáp án C sai vì hai đường thẳng đó có thể chéo nhau.
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
Đáp án A sai vì nếu đường thẳng đó cắt mặt phẳng chứa hai đường thẳng còn lại tại chính giao điểm của hai đường thẳng thì ba đường thẳng đó cũng không đồng quy.
Do đó đáp án C và D cũng sai.
Cho tứ diện $ABCD$ đều cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$. Góc giữa $AO$ và $CD$ bằng bao nhiêu?
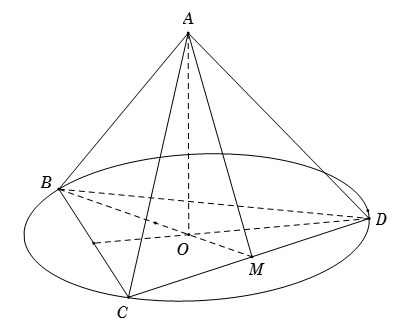
Gọi \(M\) là trung điểm của \(CD\).
Vì $ABCD$ là tứ diện đều nên \(AM \bot CD,\,\,OM \bot CD.\)
Ta có \(\overrightarrow {CD} .\overrightarrow {AO} = \overrightarrow {CD} .\left( {\overrightarrow {AM} + \overrightarrow {MO} } \right) = \overrightarrow {CD} .\overrightarrow {AM} + \overrightarrow {CD} .\overrightarrow {MO} = 0.\)
Suy ra \(\overrightarrow {AO} \bot \overrightarrow {CD} \) nên số đo góc giữa hai đường thẳng $AO$ và $CD$ bằng \({90^0}.\)
Trong các khẳng định sau, khẳng định nào đúng ?
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia nên nếu $a$ và $b$ song song, nếu $a$ vuông góc với $c$ thì $b$ cũng vuông góc với $c$
Đán án A sai vì A'B' và B'C' cùng vuông góc với BB' nhưng A'B' và B'C' lại không song song với nhau.
Đáp án B sai vì: A'B' và B'D' cùng vuông góc với BB' nhưng A'B' và B'D' lại không vuông góc với nhau.
Đáp án C sai vì: AB và CD là hai đường thẳng phân biệt, AD vuông góc với hai đường thẳng này nhưng cả 3 đường thẳng đồng phẳng
Cho hình chóp $S.ABC$ có $SA = SB = SC$ và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \)?
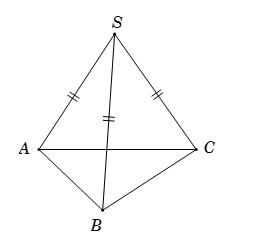
Ta có $\overrightarrow {SC} .\overrightarrow {AB} = \overrightarrow {SC} .\left( {\overrightarrow {SB} - \overrightarrow {SA} } \right) = \overrightarrow {SC} .\overrightarrow {SB} - \overrightarrow {SC} .\overrightarrow {SA} $
$\begin{array}{l} = \left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {SB} } \right|.\cos \left( {\overrightarrow {SC} .\overrightarrow {SB} } \right) - \left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {SA} } \right|.\cos \left( {\overrightarrow {SC} .\overrightarrow {SA} } \right)\\ = SC.SB.\cos \widehat {BSC} - SC.SA.\cos \widehat {ASC}.\end{array}$
Mà $SA = SB = SC$ và $\widehat {BSC} = \widehat {ASC}$\( \Rightarrow \overrightarrow {SC} .\overrightarrow {AB} = 0\).
Do đó $\left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = 90^\circ $.
Cho hình chóp \(S.ABC\) có \(AB = AC\) và \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng chéo nhau \(SA\) và \(BC.\)
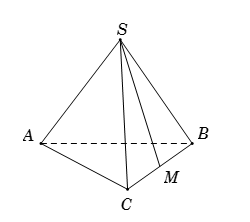
Xét \(\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .\left( {\overrightarrow {SC} - \overrightarrow {SB} } \right) = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \)
$ = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \left( {\overrightarrow {SA} ,\overrightarrow {SC} } \right) - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|.\cos \widehat {SAB}$
$ = SA.SC.\cos \widehat {ASC} - SA.SB.\cos \widehat {ASB}.$ \(\left( 1 \right)\)
Ta có \(\left\{ \begin{array}{l}SA{\rm{ chung}}\\AB = AC\\\widehat {SAB} = \widehat {SAC}\end{array} \right. \Rightarrow \Delta SAB = \Delta SAC{\rm{ }}\left( {c - g - c} \right)\).
Suy ra \(\left\{ \begin{array}{l}SC = SB\\\widehat {ASC} = \widehat {ASB}\end{array} \right.\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(\overrightarrow {SA} .\overrightarrow {BC} = 0\). Vậy \(SA \bot BC\).
Cho hai đường thẳng phân biệt $a,{\rm{ }}b$ và mặt phẳng $\left( P \right)$ , trong đó $a \bot \left( P \right)$. Mệnh đề nào sau đây là sai?
Dễ thấy các đáp án A, B, C đều đúng.
Đáp án D: Vì \(b\) có thể nằm trong mặt phẳng $\left( P \right)$ nên D sai.
Cho tứ diện đều $ABCD$, $M$ là trung điểm của cạnh $BC$. Khi đó $\cos \left( {AB,DM} \right)$ bằng :
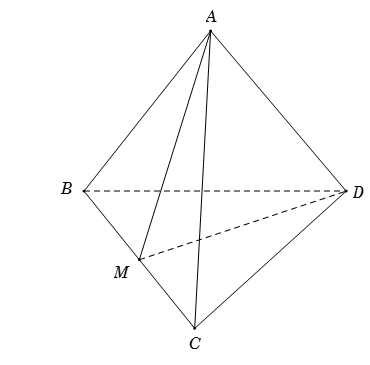
Giả sử cạnh của tứ diện là \(a\).
Tam giác \(BCD\) đều \( \Rightarrow DM = \dfrac{{a\sqrt 3 }}{2}\).
Tam giác \(ABC\) đều \( \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2}\).
Ta có: $\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {DM} } \right|}} = \dfrac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{a.\dfrac{{a\sqrt 3 }}{2}}}$
Mặt khác: $\overrightarrow {AB} .\overrightarrow {DM} = \overrightarrow {AB} \left( {\overrightarrow {AM} - \overrightarrow {AD} } \right) = \overrightarrow {AB} .\overrightarrow {AM} - \overrightarrow {AB} .\overrightarrow {AD} $
$\begin{array}{l} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AM} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right)\\ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos 30^\circ - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos 60^\circ \\ = a.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} - a.a.\dfrac{1}{2} = \dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}}}{4}\end{array}$
$ \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \dfrac{{\sqrt 3 }}{6} > 0 $ $\Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \left( {AB,DM} \right) $ $\Rightarrow \cos \left( {AB,DM} \right) = \dfrac{{\sqrt 3 }}{6}$.
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có cạnh $a$. Gọi $M$ là trung điểm $AD$. Giá trị \(\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} \) là:
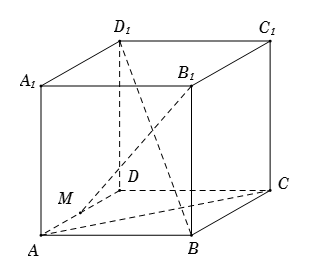
Ta có $\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} = \left( {\overrightarrow {{B_1}B} + \overrightarrow {BA} + \overrightarrow {AM} } \right)\left( {\overrightarrow {BA} + \overrightarrow {AD} + \overrightarrow {D{D_1}} } \right)$
\( = \underbrace {\overrightarrow {B{B_1}} .\overrightarrow {BA} }_{ = 0} + \underbrace {\overrightarrow {B{B_1}} .\overrightarrow {AD} }_{ = 0} + \overrightarrow {{B_1}B} .\overrightarrow {D{D_1}} + {\overrightarrow {BA} ^2} + \underbrace {\overrightarrow {BA} .\overrightarrow {AD} }_{ = 0}\) \( + \underbrace {\overrightarrow {BA} .\overrightarrow {D{D_1}} }_{ = 0}\)\( + \underbrace {\overrightarrow {AM} .\overrightarrow {BA} }_{ = 0} + \overrightarrow {AM} .\overrightarrow {AD} + \underbrace {\overrightarrow {AM} .\overrightarrow {D{D_1}} }_{ = 0}\)
$ = \overrightarrow {{B_1}B} .\overrightarrow {D{D_1}} + {\overrightarrow {BA} ^2} + \overrightarrow {AM} .\overrightarrow {AD} $$ = - {a^2} + {a^2} + \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}}}{2}$.
Cho hình lập phương $ABCD.EFGH$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
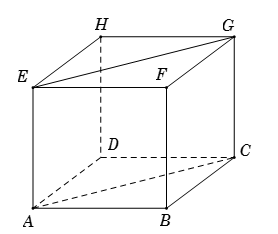
Vì $\cos \left( {AB,CD} \right) = \dfrac{{\left| { - \dfrac{1}{4}AB.CD} \right|}}{{AB.CD}} = \dfrac{1}{4}$ (\(AEGC\) là hình chữ nhật) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^0}\) (\(ABCD\) là hình vuông).
Trong không gian cho hai tam giác đều $ABC$ và $ABC'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$ . Tứ giác $MNPQ$ là hình gì?
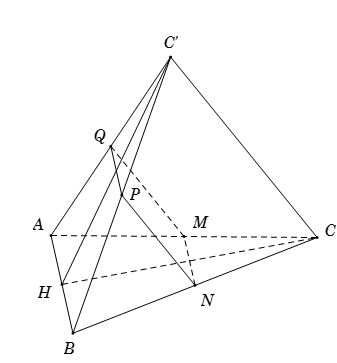
Vì $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$
\( \Rightarrow \left\{ \begin{array}{l}PQ = MN = \dfrac{1}{2}AB\\PQ//AB//MN\end{array} \right.\)\( \Rightarrow \) \(MNPQ\) là hình bình hành.
Gọi \(H\) là trung điểm của \(AB\). Vì hai tam giác $ABC$ và $ABC'$ đều nên \(\left\{ \begin{array}{l}CH \bot AB\\C'H \bot AB\end{array} \right..\)
Suy ra \(AB \bot \left( {CHC'} \right)\). Do đó \(AB \bot CC'\).
Ta có \(\left\{ \begin{array}{l}PQ{\rm{//}}AB\\PN{\rm{//}}CC'\\AB \bot CC'\end{array} \right. \Rightarrow PQ \bot PN\) .
Vậy tứ giác $MNPQ$là hình chữ nhật.
Cho tứ diện$ABCD$ có $AB = AC = AD$ và \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \)?
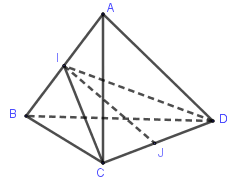
Xét tam giác\(ICD\) có \(J\) là trung điểm đoạn \(CD\).
Ta có: \(\overrightarrow {IJ} = \dfrac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right)\)
Vì tam giác \(ABC\) có \(AB = AC\) và \(\widehat {BAC} = 60^\circ \)
Nên tam giác \(ABC\)đều. Suy ra: \(CI \bot AB\)
Tương tự ta có tam giác \(ABD\) đều nên \(DI \bot AB\).
Xét \(\overrightarrow {IJ} .\overrightarrow {AB} = \dfrac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right).\overrightarrow {AB} = \dfrac{1}{2}\overrightarrow {IC} .\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {ID} .\overrightarrow {AB} = \overrightarrow 0 \).
Suy ra \(\overrightarrow {IJ} \bot \overrightarrow {AB} \). Hay góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \) bằng \({90^0}\).
Cho tứ diện $ABCD$ có $AC = a,{\rm{ }}BD = 3a$. Gọi $M{,^{}}N$ lần lượt là trung điểm của $AD$ và $BC$. Biết $AC$ vuông góc với $BD$. Tính $MN$.
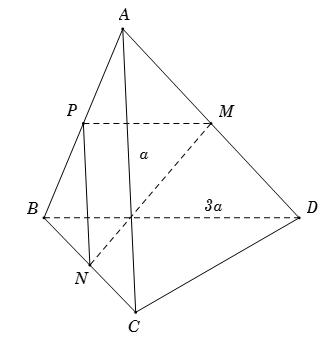
Gọi \(P\) là trung điểm của \(AB\) \( \Rightarrow PN,PM\) lần lượt là đường trung bình của tam giác \(\Delta ABC\) và \(\Delta ABD\). Suy ra \(\left\{ \begin{array}{l}PN = \dfrac{1}{2}AC = \dfrac{a}{2}\\PM = \dfrac{1}{2}BD = \dfrac{{3a}}{2}\end{array} \right..\)
Ta có \(AC \bot BD \Rightarrow PN \bot PM\) hay tam giác \(\Delta PMN\) vuông tại \(P\)
Do đó \(MN = \sqrt {P{N^2} + P{M^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{9{a^2}}}{4}} = \dfrac{{a\sqrt {10} }}{2}.\)

