Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với đáy, \(SA = a\). Khoảng cách giữa đường thẳng \(CD\) và mặt phẳng \(\left( {SAB} \right)\) là
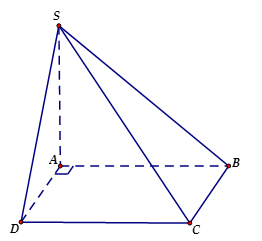
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD\).
Ta có: $\left\{ \begin{array}{l}SA \bot AD\\AB \bot AD\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right)$$ \Rightarrow d\left( {D,\,\left( {SAB} \right)} \right) = DA$.
Vì \(CD//AB \subset \left( {SAB} \right)\) nên $d\left( {CD,\,\left( {SAB} \right)} \right)$$ = d\left( {D,\,\left( {SAB} \right)} \right) = DA = a$
Cho hình chóp S.ABCD có đáy là hình thang vuông \(\left( {AB//CD} \right)\); SD vuông góc với mặt đáy $\left( {ABCD} \right);{\rm{ }}AD = 2a;{\rm{ }}SD = a\sqrt 2 .$ Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).
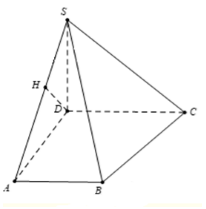
Do $AB//CD$ do đó $d\left( {CD;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right)$
Dựng $DH \bot SA$ ta có:
$\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{AB \bot AD}\\{AB \bot SD}\end{array}} \right. \Rightarrow AB \bot \left( {SAD} \right) \Rightarrow AB \bot DH}\\{\left\{ {\begin{array}{*{20}{l}}{DH \bot AB}\\{DH \bot SA}\end{array}} \right. \Rightarrow DH \bot \left( {SAB} \right) \Rightarrow d\left( {D;\left( {SAB} \right)} \right) = DH}\end{array}$
Áp dụng hệ thức lượng trong tam giác vuông
$ \Rightarrow d = DH = \dfrac{{SD.DA}}{{\sqrt {S{D^2} + D{A^2}} }} = \dfrac{{2a}}{{\sqrt 3 }}$
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,{\rm{ }}AB = 3a,{\rm{ }}BC = 4a.\) Cạnh bên \(SA\) vuông góc với đáy. Góc tạo bởi giữa \(SC\) và đáy bằng \(60^\circ \). Gọi \(M\) là trung điểm của \(AC\), \(N\) là trung điểm của \(BC\). Tính khoảng cách giữa đường thẳng \(AB\) và mặt phẳng \(\left( {SMN} \right)\).
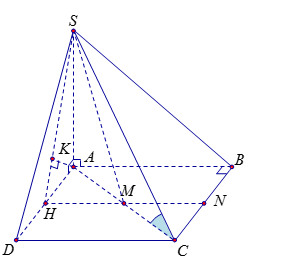
\(AC = 5a,{\rm{ }}SA = 5a\sqrt 3 \).
Ta có: \(AB{\rm{//}}\left( {SMN} \right) \Rightarrow d\left( {AB,\left( {SMN} \right)} \right) = d\left( {A,\left( {SMN} \right)} \right)\).
Dựng \(AH \bot MN\) tại \(H\) trong \(\left( {ABC} \right)\).
Dựng \(AK \bot SH\) tại \(K\) trong \(\left( {{\rm{S}}AH} \right)\).
\( \Rightarrow AK \bot \left( {SMN} \right)\) tại \(K\) nên \(d\left( {A,\left( {SMN} \right)} \right) = AK\)$ \Rightarrow d\left( {AB,\left( {SMN} \right)} \right) = AK$.
\(AH = NB = 2a\).
\(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{75{a^2}}} = \dfrac{{79}}{{300{a^2}}}\) \( \Rightarrow AK = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\) cạnh \(a\), \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SO = a.\) Khoảng cách giữa đường thẳng \(AB\) và mặt phẳng \(\left( {SCD} \right)\) bằng
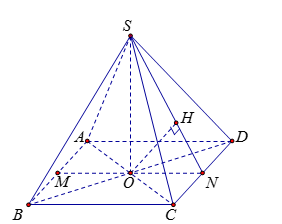
Gọi \(M,N\) lần lượt là trung điểm của các cạnh$AB,CD$; $H$ là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì $AB{\rm{//}}CD$ nên \(d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\) (vì \(O\) là trung điểm đoạn \(MN\))
Ta có $\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH$
Khi đó $\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.$
Tam giác \(SON\) vuông tại \(O\) nên $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{S^2}}} = \dfrac{1}{{\dfrac{{{a^2}}}{4}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{{a^2}}} \Rightarrow OH = \dfrac{a}{{\sqrt 5 }}$
Vậy \(d\left( {AB,\left( {SCD} \right)} \right) = 2OH = \dfrac{{2a\sqrt 5 }}{5}\).
Cho lăng trụ \(ABC.A'B'C'\) có các mặt bên là hình vuông cạnh \(a\). Gọi \(D\), \(E\) lần lượt là trung điểm các cạnh \(BC\), \(A'C'\). Tính khoảng cách giữa đường thẳng \(DE\) và mặt phẳng \(\left( {ABB'A'} \right)\) theo \(a\).
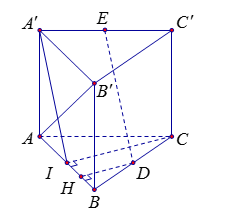
Gọi \(I\) là trung điểm của \(AB\). Khi đó \(CI = \dfrac{{a\sqrt 3 }}{2},\)\(CI \bot \left( {ABB'A'} \right)\)
Gọi \(H\) là trung điểm của \(IB\).
Vì \(DH{\rm{//}}CI\) nên \(DH \bot \left( {ABB'A'} \right)\)
Vì $\left\{ \begin{array}{l}ID{\rm{//}}AC{\rm{//}}A'E\\ID = \dfrac{1}{2}AC = A'E\end{array} \right.$ nên tứ giác \(A'EDI\) là hình bình hành, suy ra $DE\;{\rm{//}}\;A'I \subset \left( {ABB'A'} \right)$.
Ta có $DE\;{\rm{//}}\;\left( {ABB'A'} \right)$.
Vậy \(d\left( {DE,\left( {ABB'A'} \right)} \right) = d\left( {D,\left( {ABB'A'} \right)} \right) = DH = \dfrac{{CI}}{2} = \dfrac{{a\sqrt 3 }}{4}\)
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại $A$ có $BC = 2a,{\mkern 1mu} AB = a\sqrt 3 .$ Khoảng cách từ AA' đến mặt phẳng $\left( {BCC'B'} \right)$ là:
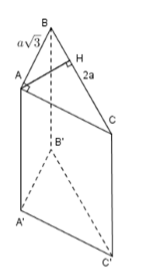
Hạ đường cao AH xuống cạnh BC. Khi đó khoảng cách từ AA' đến $\left( {BCC'B'} \right)$ chính là độ dài AH. Ta có $\Delta ABC$ vuông tại $A$ nên theo định lý Py-ta-go ta nhận được
$A{C^2} = B{C^2} - A{B^2} = {\left( {2a} \right)^2} - {\left( {a\sqrt 3 } \right)^2} = {a^2} \Rightarrow AC = a.$
Áp dụng hệ thức trong tam giác vuôngABC ta nhận được
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \Rightarrow AH = \dfrac{{\sqrt 3 a}}{2}.$
Cho lăng trụ đứng tam giác \(ABC.A'B'C'\) có đáy là một tam giác vuông cân tại \(B\), \(AB = BC = a\), \(AA' = a\sqrt 2 \), \(M,E\) là trung điểm \(BC,BB'\). Tính khoảng cách giữa đường thẳng \(B'C\) và mặt phẳng \(\left( {AME} \right)\).
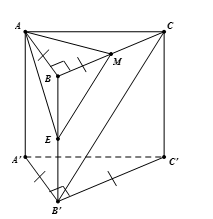
Ta có: $EM{\kern 1pt} \;{\rm{//}}\;B'C$\( \Rightarrow B'C{\kern 1pt} \;{\rm{//}}\;(AME)\)
\( \Rightarrow d\left( {B'C,\left( {AME} \right)} \right) = d\left( {C,\left( {AME} \right)} \right) = d\left( {B,\left( {AME} \right)} \right)\)
Xét khối chóp \(BAME\) có các cạnh \(BE\), \(AB\), \(BM\) đôi một vuông góc với nhau nên
\(\dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{M{B^2}}} + \dfrac{1}{{E{B^2}}}\)\( \Leftrightarrow \dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \dfrac{7}{{{a^2}}}\)\( \Leftrightarrow {d^2}\left( {B,\left( {AME} \right)} \right) = \dfrac{{{a^2}}}{7}\)
\( \Leftrightarrow d\left( {B,\left( {AME} \right)} \right) = \dfrac{a}{{\sqrt 7 }}\).
Cho hình lập phương ABCD. A’B’C’D’ có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (AB’D’) và (BC’D) bằng:
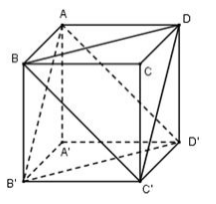
Dễ thấy BD // B’D’, BC’ // AD’ nên (AB’D’) // (BC’D)
$ \Rightarrow d\left( {\left( {AB'D'} \right);\left( {BC'D} \right)} \right) = d\left( {C';\left( {AB'D'} \right)} \right) = \dfrac{{3{V_{C'.AB'D'}}}}{{{S_{AB'D'}}}}$
Ta có :
$\begin{array}{l}{V_{C'.AB'D'}} = {V_{A.B'C'D'}} = \dfrac{1}{3}AA'.{S_{B'C'D'}} = \dfrac{1}{3}AA'.\dfrac{1}{2}B'C'.C'D'\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{1}{6}{V_{ABCD.A'B'C'D'}} = \dfrac{1}{6}{.2^3} = \dfrac{4}{3}\end{array}$
Tam giác AB’D’ có $AB' = AD' = B'D' = 2\sqrt 2 \Rightarrow \Delta AB'D'$ là tam giác đều cạnh
$2\sqrt 2 \Rightarrow {S_{AB'D'}} = \dfrac{{{{\left( {2\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = 2\sqrt 3 $
Vậy $d\left( {C';\left( {AB'D'} \right)} \right) = \dfrac{{3.\dfrac{4}{3}}}{{2\sqrt 3 }} = \dfrac{2}{{\sqrt 3 }} \Rightarrow d\left( {\left( {AB'D'} \right);\left( {BC'D} \right)} \right) = \dfrac{2}{{\sqrt 3 }}$.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 \), \(AA' = 2a\). Tính khoảng cách giữa đường thẳng \(BD\) và mặt phẳng \(\left( {CB'D'} \right)\).
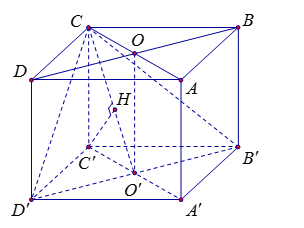
Gọi \(O,\,\)\(O'\) lần lượt là tâm của hai mặt đáy. Khi đó tứ giác \(COO'C'\)là hình bình hành và \(C'O' = \dfrac{{AC}}{2} = a\)
Do \(BD\;{\rm{//}}\;B'D'\)$ \Rightarrow BD\;{\rm{//}}\;\left( {CB'D'} \right)$ nên \(d\left( {BD;\left( {CB'D'} \right)} \right) = d\left( {O;\left( {CB'D'} \right)} \right) = d\left( {C';\left( {CB'D'} \right)} \right)\).
Ta có : \(\left\{ \begin{array}{l}B'D' \bot A'C'\\B'D' \bot CC'\end{array} \right. \Rightarrow B'D' \bot \left( {COO'C'} \right)\)\( \Rightarrow \left( {CB'D'} \right) \bot \left( {COO'C'} \right)\)
Lại có \(\left( {CB'D'} \right) \cap \left( {COO'C'} \right) = CO'\).
Trong \(\Delta CC'O'\) hạ \(C'H \bot CO' \Rightarrow C'H \bot \left( {CB'D'} \right)\)\( \Rightarrow d\left( {BD;\,CD'} \right) = C'H\)
Khi đó : \(\dfrac{1}{{C'{H^2}}} = \dfrac{1}{{C{{C'}^2}}} + \dfrac{1}{{C'{{O'}^2}}} = \dfrac{1}{{{{\left( {2a} \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{4{a^2}}}\)\( \Rightarrow C'H = \dfrac{{2\sqrt 5 a}}{5}\).
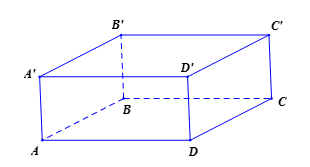
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3,AD = 4,AA' = 5\). Khoảng cách giữa hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {A'B'C'D'} \right)\)bằng
Ta có \(d\left( {\left( {ABCD} \right),\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = 5\)
Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh bằng 10. Tính khoảng cách giữa hai mặt phẳng (ADD’A’) và (BCC’B’).
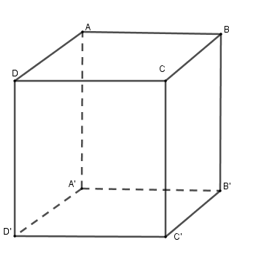
Vì \(ABCD.{A}'{B}'{C}'{D}'\) là hình lập phương nên \(\left( AD{D}'{A}' \right)\)// \(\left( BC{C}'{B}' \right)\).
Khi đó \(d\left( \left( AD{D}'{A}' \right);\left( BC{C}'{B}' \right) \right)=d\left( A;\left( BC{C}'{B}' \right) \right)\)
Mà \(AB\bot \left( BC{C}'{B}' \right)\) nên \(d\left( A;\left( BC{C}'{B}' \right) \right)=AB=10\).
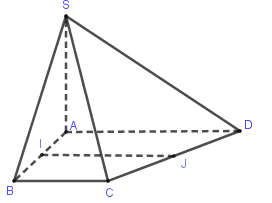
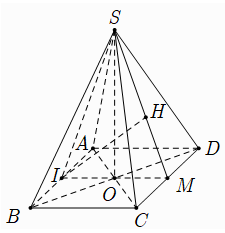
Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$, đáy $ABCD$ là hình thang vuông tại \(A,B\) có $AB = a$. Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Tính khoảng cách giữa đường thẳng $IJ$ và $\left( {SAD} \right)$.
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot IA\), mà \(IA \bot AD\) nên \(IA \bot \left( {SAD} \right)\)
Lại có $IJ$// $AD$ nên $IJ$// $\left( {SAD} \right)$
$ \Rightarrow d\left( {IJ;\left( {SAD} \right)} \right) = d\left( {I;\left( {SAD} \right)} \right) = IA = \dfrac{a}{2}$
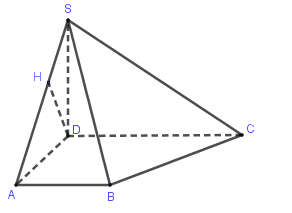
Cho hình thang vuông $ABCD$ vuông ở $A$ và $D$, $AD = 2a.$ Trên đường thẳng vuông góc với $\left( {ABCD} \right)$ tại $D$ lấy điểm $S$ với $SD = a\sqrt 2 .$ Tính khỏang cách giữa đường thẳng $DC$ và $\left( {SAB} \right)$.
Vì $DC$// $AB$ nên $DC$// $\left( {SAB} \right)$
$ \Rightarrow d\left( {DC;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right)$.
Kẻ $DH \bot SA$, do $AB \bot AD$, $AB \bot SD$ nên $AB \bot \left( {SAD} \right) \Rightarrow DH \bot AB$ suy ra $d\left( {D;\left( {SAB} \right)} \right) = DH$.
Trong tam giác vuông $SAD$ ta có:
$\begin{array}{l}
DH.SA = DS.DA\\
\Leftrightarrow DH = \frac{{DS.DA}}{{SA}} = \frac{{DS.DA}}{{\sqrt {S{D^2} + D{A^2}} }}\\
= \frac{{a\sqrt 2 .2a}}{{\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {2a} \right)}^2}} }} = \frac{{2a\sqrt 3 }}{3} = \frac{{2a}}{{\sqrt 3 }}\\
\Rightarrow d\left( {DC,\left( {SAB} \right)} \right) = \frac{{2a}}{{\sqrt 3 }}
\end{array}$
Cho hình chóp $O.ABC$ có đường cao $OH = \dfrac{{2a}}{{\sqrt 3 }}$. Gọi $M$ và $N$ lần lượt là trung điểm của $OA$ và $OB.$ Khoảng cách giữa đường thẳng $MN$ và $\left( {ABC} \right)$ bằng:
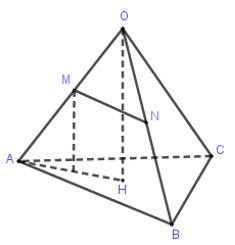
Vì $M$ và $N$ lần lượt là trung điểm của $OA$ và $OB$ nên $MN//AB \Rightarrow MN//\left( {ABC} \right)$.
Ta có: \(d\left( {MN;\left( {ABC} \right)} \right) = d\left( {M;\left( {ABC} \right)} \right) \)
Vì \(OM\) cắt \((ABC)\) tại \(A\) và \(OA=2MA\) nên \(d\left( {M;\left( {ABC} \right)} \right)= \dfrac{1}{2}OH = \dfrac{{a\sqrt 3 }}{3}\).
Cho hình chóp tứ giác đều $S.ABCD$ có $AB = SA = 2a.$ Khoảng cách từ đường thẳng $AB$ đến $\left( {SCD} \right)$ bằng bao nhiêu?
Gọi \(I,M\) lần lượt là trung điểm cạnh \(AB\) và \(CD\) thì \(\left\{ \begin{array}{l}CD \bot IM\\CD \bot SM\end{array} \right. \Rightarrow CD \bot (SIM)\)
Vẽ \(IH \bot SM\) tại \(H \in SM\)thì \(IH \bot (SCD)\)
Mà \(AB//CD \subset \left( {SCD} \right)\Rightarrow AB// (SCD)\)
\( \Rightarrow d\left( {AB,(SCD)} \right) = d\left( {I,(SCD)} \right) = IH = \dfrac{{SO.IM}}{{SM}}\)
\(\Delta SAB\) đều cạnh \(2a \Rightarrow SI = a\sqrt 3 \Rightarrow SM = a\sqrt 3 \)
Và \(OM = \dfrac{1}{2}IM = a \Rightarrow SO = \sqrt {S{M^2} - O{M^2}} = a\sqrt 2 \)
Cuối cùng \(d\left( {AB,(SCD)} \right) = \dfrac{{SO.IM}}{{SM}} = \dfrac{{a\sqrt 2 .2a}}{{a\sqrt 3 }} = \dfrac{{2a\sqrt 6 }}{3}\)
Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có cạnh đáy bằng $a$. Gọi $M$, $N$, $P$ lần lượt là trung điểm của $AB$, $BC$, $A'B'$. Tính khoảng cách giữa hai mặt phẳng $\left( {MNP} \right)$ và $\left( {ACC'} \right)$.
Ta có: $MM//AC,MP//A'A \Rightarrow \left( {MNP} \right)//\left( {ACC'} \right)$
$ \Rightarrow d\left( {\left( {MNP} \right);\left( {ACC'} \right)} \right) = d\left( {P;\left( {ACC'} \right)} \right) = \dfrac{1}{2}d\left( {B',\left( {ACC'} \right)} \right)$
Lại có:
\(B'O' \bot A'C',B'O' \bot CC' \Rightarrow B'O' \bot \left( {ACC'} \right)\) \( \Rightarrow d\left( {B',\left( {ACC'} \right)} \right) = B'O' = \dfrac{1}{2}B'D' = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {P,\left( {ACC'} \right)} \right) = \dfrac{1}{2}d\left( {B',\left( {ACC'} \right)} \right) = \dfrac{{a\sqrt 2 }}{4}\)
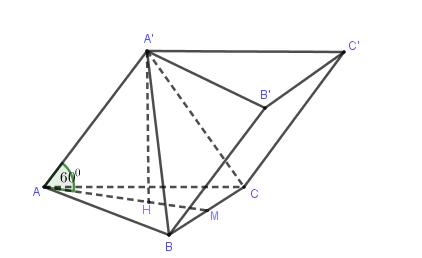
Cho hình lăng trụ tam giác $ABC.A'B'C'$ có các cạnh bên hợp với đáy những góc bằng $60^\circ $, đáy $ABC$ là tam giác đều cạnh $a$ và $A'$ cách đều $A$, $B$, $C$. Tính khoảng cách giữa hai đáy của hình lăng trụ.
Ta có: \(\left( {ABC} \right)//\left( {A'B'C'} \right) \Rightarrow d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right)\)
Vì $\Delta ABC$ đều và $AA' = A'B = A'C \Rightarrow A'ABC$ là hình chóp đều.
Gọi $A'H$ là chiều cao của lăng trụ, suy ra $H$ là trọng tâm $\Delta ABC,\widehat {A'AH} = 60^\circ $.
$ \Rightarrow d\left( {A',\left( {ABC} \right)} \right) = A'H = AH.\tan 60^\circ = \dfrac{{a\sqrt 3 }}{3}\sqrt 3 = a$.
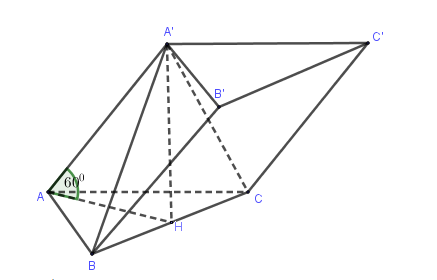
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có cạnh bên bằng $a.$ Các cạnh bên của lăng trụ tạo với mặt đáy góc ${60^{\rm{o}}}.$ Hình chiếu vuông góc của $A'$ lên mặt phẳng $\left( {ABC} \right)$ là trung điểm của $BC$. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?
Ta có: $A'H \bot \left( {ABC} \right) \Rightarrow \widehat {A'AH} = {60^{\rm{o}}}.$
\(d\left( {\left( {A'B'C'} \right),\left( {ABC} \right)} \right) = A'H = A'A.\sin {60^{\rm{o}}} = \dfrac{{a\sqrt 3 }}{2}\)
Cho hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\). Hình chiếu \(H\) của \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) thuộc cạnh \(B'C'\). Biết khoảng cách giữa hai mặt phẳng đáy là \(\dfrac{a}{2}\). Tìm vị trí của \(H\) trên \(B'C'\).
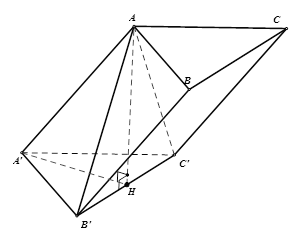
Do hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\) nên \(A'A = a\).
\(H\) là hình chiếu của \(A\) trên \(\left( {A'B'C'} \right)\) nên \(AH \bot \left( {A'B'C'} \right) \Rightarrow d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = AH = \dfrac{a}{2}\)
\(\Delta A'HA\) vuông tại \(H\) nên \(A'H = \sqrt {A'{A^2} - A{H^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
Mặt khác \(\Delta A'B'C'\) đều cạnh \(a\) nên đường cao \(A'H' = \dfrac{{a\sqrt 3 }}{2}\) ($H'$ là trung điểm của $B'C'$)
Từ đó \(A'H = A'H'\) và \(H,H' \in B'C'\) nên \(H \equiv H'\).
Vậy \(H\) là trung điểm của \(B'C' \Rightarrow HB' = \dfrac{1}{2}B'C'\).
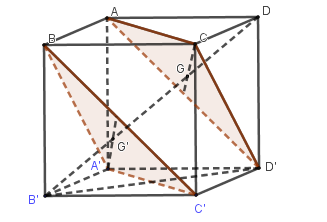
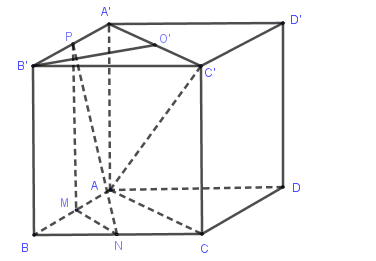
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Khoảng cách giữa hai mặt phẳng \((ACD')\) và \((BA'C')\) bằng
Gọi \(G,G'\) là trọng tâm các tam giác \(ACD',BA'C'\).
Khi đó \(DG \bot \left( {ACD'} \right),B'G' \bot \left( {BA'C'} \right)\) vì các hình chóp \(D.ACD'\) và \(B'.BA'C'\) là hình chóp đều.
Ta có: \(AC \bot \left( {BDD'B'} \right) \Rightarrow AC \bot DB'\)
Lại có \(CD' \bot \left( {ADC'B'} \right) \Rightarrow CD' \bot DB'\).
Do đó \(DB' \bot \left( {ACD'} \right)\).
Tương tự \(DB' \bot \left( {BA'C'} \right)\) nên \(\left( {ACD'} \right)//\left( {BA'C'} \right)\) và \(G,G' \in DB'\).
Do đó \(GG'\) vuông góc cả hai mặt phẳng \(\left( {ACD'} \right),\left( {BA'C'} \right)\).
Vậy khoảng cách giữa hai mặt đó là \(GG'\).