Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại $A$ có $BC = 2a,{\mkern 1mu} AB = a\sqrt 3 .$ Khoảng cách từ AA' đến mặt phẳng $\left( {BCC'B'} \right)$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
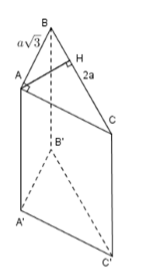
Hạ đường cao AH xuống cạnh BC. Khi đó khoảng cách từ AA' đến $\left( {BCC'B'} \right)$ chính là độ dài AH. Ta có $\Delta ABC$ vuông tại $A$ nên theo định lý Py-ta-go ta nhận được
$A{C^2} = B{C^2} - A{B^2} = {\left( {2a} \right)^2} - {\left( {a\sqrt 3 } \right)^2} = {a^2} \Rightarrow AC = a.$
Áp dụng hệ thức trong tam giác vuôngABC ta nhận được
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \Rightarrow AH = \dfrac{{\sqrt 3 a}}{2}.$
Hướng dẫn giải:
Hạ đường cao AH xuống cạnh BC. Khi đó khoảng cách từ AA' đến $\left( {BCC'B'} \right)$ chính là độ dài AH. Áp dụng định lý Py-ta-go và hệ thức trong tam giác vuông ABC để tìm AH.
