Cho chóp đều \(S.ABCD\) có cạnh đáy bằng \(2\), cạnh bên bằng \(3\). Gọi \(\varphi \) là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?

Gọi \(O\) là tâm mặt đáy \(\left( {ABCD} \right)\) , suy ra \(SO \bot \left( {ABCD} \right)\).
Vì \(SO \bot \left( {ABCD} \right)\), suy ra \(OA\) là hình chiếu của \(SA\) trên mặt phẳng \(\left( {ABCD} \right)\).
Do đó \(\widehat {\left( {SA,\left( {ABCD} \right)} \right)} = \widehat {\left( {SA,AO} \right)} = \widehat {SAO}.\)
Đáy ABCD là hình vuông nên \(BO=OA=\sqrt 2\)
Tam giác vuông \(SOA\), có \(\tan \widehat {SAO} = \dfrac{{SO}}{{AO}} = \dfrac{{\sqrt {S{B^2} - B{O^2}} }}{{\sqrt 2}} = \dfrac{{\sqrt {14} }}{2}.\)
Cho hình chóp $S.ABC$ có đáy \(ABC\) là tam giác vuông tại \(A\), \(\widehat {ABC} = {60^ \circ }\), tam giác \(SBC\) là tam giác đều có cạnh bằng \(2a\). Biết hình chiếu của \(S\) lên mặt phẳng đáy trùng với trung điểm của \(BC\). Tính góc giữa đường thẳng \(SA\) và mặt phẳng đáy \(\left( {ABC} \right)\)
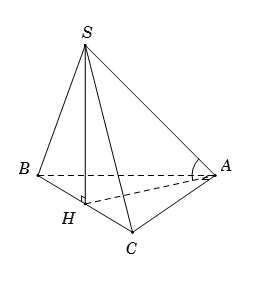
Gọi \(H\) là trung điểm của \(BC\), suy ra \(SH \bot \left( {ABC} \right)\).
Vì \(SH \bot \left( {ABC} \right)\) nên \(HA\) là hình chiếu của \(SA\) trên mặt phẳng \(\left( {ABC} \right)\).
Do đó \(\widehat {\left( {SA,\left( {ABC} \right)} \right)} = \widehat {\left( {SA,AH} \right)} = \widehat {SAH}\).
Tam giác \(SBC\) đều cạnh \(2a\) nên \(SH = a\sqrt 3 .\)
Tam giác \(ABC\) vuông tại \(A\) nên \(AH = \dfrac{1}{2}BC = a.\)
Tam giác vuông \(SAH\), có \(\tan \widehat {SAH} = \dfrac{{SH}}{{AH}} = \sqrt 3 \), suy ra \(\widehat {SAH} = {60^0}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có cạnh \(AB = a\), \(BC = 2a\), cạnh bên \(SA\) vuông góc với đáy, \(SA = a\sqrt {15} \). Tính góc tạo bởi đường thẳng \(SC\) và mặt phẳng \(\left( {ABD} \right)\).
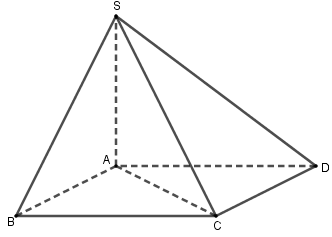
Do \(SA \bot \left( {ABCD} \right)\) nên \(\widehat {SC,\left( {ABD} \right)} = \widehat {SC,\left( {ABCD} \right)} = \widehat {SC,AC} = \widehat {SCA}\)
Xét tam giác vuông \(SAC\), ta có \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{B^2} + B{C^2}} }} = \sqrt 3 \).
Suy ra \(\widehat {SCA} = {60^0}\).
Cho lăng trụ \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = {60^0}\). Hình chiếu vuông góc của \(B'\) xuống mặt đáy trùng với giao điểm hai đường chéo của đáy và cạnh bên \(BB' = a\). Tính góc giữa cạnh bên và mặt đáy.
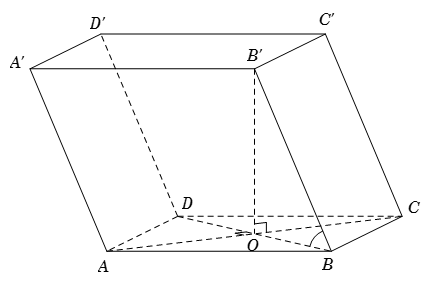
Gọi \(O = AC \cap BD\). Theo giả thiết \(B'O \bot \left( {ABCD} \right)\).
Do đó \(\widehat {BB',\left( {ABCD} \right)} = \widehat {BB',BO} = \widehat {B'BO}\).
Từ giả thiết suy ra tam giác \(ABD\) đều cạnh \(a\), suy ra \(BO = \dfrac{1}{2}BD = \dfrac{a}{2}\).
Tam giác vuông \(B'BO\), có \(\cos \widehat {B'BO} = \dfrac{{BO}}{{BB'}} = \dfrac{1}{2} \Rightarrow \widehat {B'BO} = {60^0}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh bằng \(4a\). Cạnh bên \(SA = 2a\). Hình chiếu vuông góc của đỉnh \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm của \(H\) của đoạn thẳng \(AO\). Gọi \(\alpha \) là góc giữa \(SD\) và mặt phẳng $\left( {ABCD} \right)$. Mệnh đề nào sau đây đúng?

Vì \(SH \bot \left( {ABCD} \right)\) nên hình chiếu vuông góc của \(SD\) trên mặt phẳng \(\left( {ABCD} \right)\) là \(HD\).
Do đó $\widehat {SD,\left( {ABCD} \right)} = \widehat {\left( {SD,HD} \right)} = \widehat {SDH}.$
Tính được \(SH = \sqrt {S{A^2} - A{H^2}} = a\sqrt 2 .\)
Trong tam giác \(ADH\), có \(DH = \sqrt {A{H^2} + A{D^2} - 2AH.AD.\cos {{45}^0}} = a\sqrt {10} .\)
Tam giác vuông \(SHD\), có \(\tan \widehat {SDH} = \dfrac{{SH}}{{HD}} = \dfrac{{\sqrt 5 }}{5}.\)
Cho hình chóp \(S.ABC\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tâm \(O\). Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(\varphi \) là góc giữa \(SO\) và mặt phẳng \(\left( {ABCD} \right)\). Mệnh đề nào sau đây đúng?
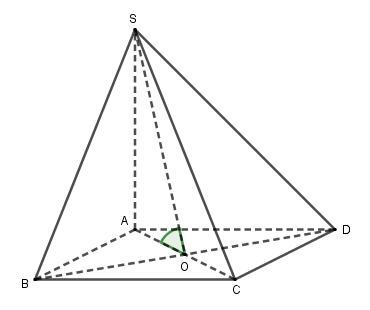
Bước 1:
Vì \(SA \bot \left( {ABCD} \right)\) nên hình chiếu vuông góc của \(SO\) trên mặt đáy \(\left( {ABCD} \right)\) là \(AO\).
Do đó \(\widehat {\left( {SO,\left( {ABCD} \right)} \right)} = \widehat {\left( {SO,OA} \right)} = \widehat {SOA}.\)
Bước 2:
Trong tam giác vuông \(SAO\), ta có \(\tan \widehat {SOA} = \dfrac{{SA}}{{OA}} = 2\sqrt 2 .\)
Vậy \(SO\) hợp với mặt đáy \(\left( {ABCD} \right)\) một góc nhọn \(\varphi \) thỏa mãn \(\tan \varphi = 2\sqrt 2 \).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a,\) \(AD = a\sqrt 3 \). Hình chiếu vuông góc \(H\) của \(S\) trên mặt đáy trùng với trọng tâm tam giác \(ABC\) và \(SH = \dfrac{a}{2}\). Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm các cạnh \(BC\) và \(SC\). Gọi \(\alpha \) là góc giữa đường thẳng \(MN\) với mặt đáy \(\left( {ABCD} \right)\). Mệnh đề nào sau đây đúng?

Ta có \(MN\parallel SB\). Do đó \(\widehat {MN,\left( {ABCD} \right)} = \widehat {SB,\left( {ABCD} \right)}\).
Do \(SH \bot \left( {ABCD} \right)\) nên \(\widehat {MN,\left( {ABCD} \right)} = \widehat {SB,\left( {ABCD} \right)} = \widehat {SB,HB} = \widehat {SBH}\).
Ta có \(BD = \sqrt {A{B^2} + A{D^2}} = 2a\); \(BH = \dfrac{{BD}}{3} = \dfrac{{2a}}{3}\).
Tam giác \(SHB\), có \(\tan \widehat {SBH} = \dfrac{{SH}}{{BH}} = \dfrac{3}{4}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\). Cạnh bên \(SA\) vuông góc với đáy, góc gữa \(SC\) và mặt đáy \(\left( {ABCD} \right)\) bằng \({45^0}\). Gọi \(\varphi \) là góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {SAC} \right)\). Mệnh đề nào sau đây đúng?

Xác định \({45^0} = \widehat {SC,\left( {ABCD} \right)} = \widehat {SC,AC} = \widehat {SCA}\), suy ra \(SA = AC = 2a\sqrt 2 \).
Gọi \(O = AC \cap BD\), ta có \(\left\{ \begin{array}{l}DO \bot AC\\DO \bot SA\end{array} \right. \Rightarrow DO \bot \left( {SAC} \right)\) nên hình chiếu vuông góc của \(SD\) trên mặt phẳng \(\left( {SAC} \right)\) là \(SO\). Do đó \(\widehat {SD,\left( {SAC} \right)} = \widehat {SD,SO} = \widehat {DSO}\).
Ta có \(DO = \dfrac{1}{2}BD = a\sqrt 2 \); \(SO = \sqrt {S{A^2} + A{O^2}} = \sqrt {S{A^2} + D{O^2}} = a\sqrt {10} \).
Tam giác vuông \(SOD\), có \(\tan \widehat {DSO} = \dfrac{{OD}}{{OS}} = \dfrac{{\sqrt 5 }}{5}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Tam giác \(SAB\) đều. Gọi \(H,{\rm{ }}K\) lần lượt là trung điểm của các cạnh \(AB\) và \(AD\). Biết \(SH \bot \left( {ABC} \right)\), gọi \(\varphi \) là góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SHK} \right)\). Mệnh đề nào sau đây đúng?

Gọi \(I = HK \cap AC.\) Do \(H,{\rm{ }}K\) lần lượt là trung điểm của \(AB\) và \(AD\) nên \(HK\parallel BD\). Suy ra \(HK \bot AC\). Lại có \(AC \bot SH\) nên suy ra \(AC \bot \left( {SHK} \right)\).
Do đó \(\widehat {\left( {SA,\left( {SHK} \right)} \right)} = \widehat {\left( {SA,SI} \right)} = \widehat {ASI}.\)
Tam giác \(SIA\) vuông tại \(I\), có \(\tan \widehat {ASI} = \dfrac{{AI}}{{SI}} = \dfrac{{\dfrac{1}{4}AC}}{{\sqrt {S{A^2} - A{I^2}} }} = \dfrac{{\sqrt 7 }}{7}.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Tam giác \(SAB\) đều cạnh \(a\) và nằm trong mặt phẳng vuông góc với đáy \(\left( {ABCD} \right)\). Biết hình chiếu của \(S\) lên mặt phẳng đáy trùng với trung điểm của \(AB\). Gọi \(\varphi \) là góc giữa \(SD\) và mặt phẳng \(\left( {ABCD} \right)\). Mệnh đề nào sau đây đúng?
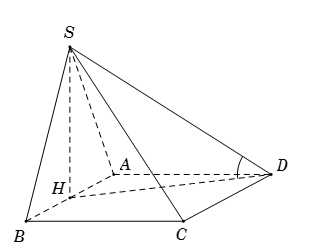
Gọi \(H\) là trung điểm \(AB\), suy ra \(SH \bot AB \Rightarrow SH \bot \left( {ABCD} \right).\) Vì \(SH \bot \left( {ABCD} \right)\) nên hình chiếu vuông góc của \(SD\) trên mặt đáy \(\left( {ABCD} \right)\) là \(HD\).
Do đó \(\widehat {SD,\left( {ABCD} \right)} = \widehat {\left( {SD,HD} \right)} = \widehat {SDH}.\)
Tam giác \(SAB\) đều cạnh \(a\) nên \(SH = \dfrac{{a\sqrt 3 }}{2}.\)
\(HD = \sqrt {A{H^2} + A{B^2}} = \dfrac{{a\sqrt 5 }}{2}.\)
Tam giác vuông \(SHD\), có \(\cot \widehat {SDH} = \dfrac{{DH}}{{SH}} = \dfrac{5}{{\sqrt {15} }}.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy \(\left( {ABCD} \right)\) và \(SA = 2a\). Gọi \(\varphi \) là góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SAD} \right)\). Mệnh đề nào sau đây đúng?
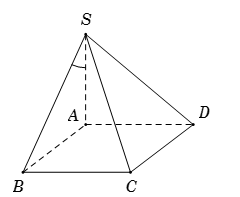
Ta có \(\left\{ \begin{array}{l}BA \bot AD\\BA \bot SA\end{array} \right. \Rightarrow BA \bot \left( {SAD} \right)\). Suy ra hình chiếu vuông góc của \(SB\) trên mặt phẳng \(\left( {SAD} \right)\) là \(SA\).
Do đó \(\widehat {SB,\left( {SAD} \right)} = \widehat {\left( {SB,SA} \right)} = \widehat {BSA}.\)
Tam giác vuông \(SAB\), ta có \(\cos \widehat {BSA} = \dfrac{{SB}}{{SA}} = \dfrac{{SA}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2\sqrt 5 }}{5}.\)
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh bằng \(2\sqrt 2 \), \(AA' = 4\). Tính góc giữa đường thẳng \(A'C\) với mặt phẳng \(\left( {AA'B'B} \right)\).
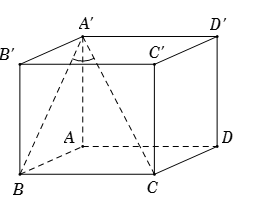
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot \left( {AA'B'B} \right)\).
Do đó \(\widehat {A'C,\left( {AA'B'B} \right)} = \widehat {\left( {A'C,A'B} \right)} = \widehat {CA'B}\).
Vì \(BC \bot \left( {AA'B'B} \right)\)\( \Rightarrow BC \bot BA'\)nên tam giác \(A'BC\) vuông tại \(B\).
Tam giác vuông \(A'BC\), có \(\tan \widehat {CA'B} = \dfrac{{BC}}{{A'B}} = \dfrac{{BC}}{{\sqrt {AA{'^2} + A{B^2}} }} = \dfrac{1}{{\sqrt 3 }}.\)
Vậy \(A'C\) tạo với mặt phẳng \(\left( {AA'B'B} \right)\) một góc \({30^0}.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại $A$ và \(B\), \(AB = BC = a\), \(AD = 2a\). Cạnh bên \(SA = a\sqrt 2 \) và vuông góc với đáy. Tính góc giữa đường thẳng \(SC\) với mặt phẳng \(\left( {SAD} \right)\).

Gọi \(M\) là trung điểm \(AD\), suy ra \(ABCM\) là hình vuông nên \(CM \bot AD\).
Ta có \(\left\{ \begin{array}{l}CM \bot AD\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAD} \right)\).
Suy ra hình chiếu vuông góc của \(SC\) trên mặt phẳng \(\left( {SAD} \right)\) là \(SM\).
Do đó \(\widehat {SC,\left( {SAD} \right)} = \widehat {SC,SM} = \widehat {CSM}\).
Tam giác vuông \(SMC\), có \(\tan \widehat {CSM} = \dfrac{{CM}}{{SM}} = \dfrac{{AB}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{1}{{\sqrt 3 }}\) \( \Rightarrow \widehat {CSM} = {30^0}\).
Đề thi THPT QG 2019 – mã đề 104
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right),\) \(SA = 2a,\) tam giác \(ABC\) vuông cân tại \(B\) và \(AB = \sqrt 2 a\) (minh họa như hình vẽ bên).
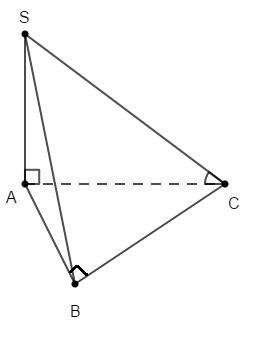
Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng
Ta có \(SA \bot \left( {ABC} \right) \Rightarrow AC\) là hình chiếu của \(SC\) trên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {SC;\left( {ABC} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\).
Tam giác \(ABC\) vuông cân tại \(B \Rightarrow AC = AB\sqrt 2 = \sqrt 2 a.\sqrt 2 = 2a\).
Tam giác \(SAC\) có \(\angle SAC = {90^0};\,\,SA = AC = 2a \Rightarrow \Delta SAC\) vuông cân tại \(A \Rightarrow \angle SCA = {45^0}\).
Vậy \(\angle \left( {SC;\left( {ABC} \right)} \right) = {45^0}\).
Cho hình chóp \(S.\,ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(\widehat {ABC} = 60^\circ \). Hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm tam giác \(ABC\). Gọi \(\varphi \) là góc giữa đường thẳng \(SB\) với mặt phẳng \(\left( {SCD} \right)\), tính \(\sin \varphi \) biết rằng \(SB = a\).
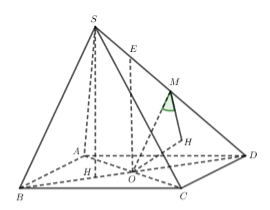
Gọi \(M\) là trung điểm của \(SD\), nhận xét góc giữa \(SB\) và \(\left( {SCD} \right)\) cũng bằng góc giữa \(OM\) và \(\left( {SCD} \right)\) (Vì \(OM//SB\))
Gọi \(H\) là hình chiếu của \(O\) trên \(\left( {SCD} \right)\) \( \Rightarrow \widehat {\left( {OM,\left( {SCD} \right)} \right)} = \widehat {\left( {OM,MH} \right)} = \widehat {OMH}\).
Trong \(\left( {SBD} \right)\) kẻ \(OE//SH\), khi đó tứ diện \(OECD\) là tứ diện vuông nên \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}} + \dfrac{1}{{O{E^2}}}\).
Ta dễ dàng tính được \(OC = \dfrac{a}{2},OD = \dfrac{{a\sqrt 3 }}{2}\).
Lại có: \(\dfrac{{OE}}{{SH}} = \dfrac{{OD}}{{HD}} = \dfrac{3}{4} \Rightarrow OE = \dfrac{3}{4}SH\), mà \(SH = \sqrt {S{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
Do đó \(OE = \dfrac{3}{4}SH = \dfrac{3}{4}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{a\sqrt 6 }}{4}\).
Suy ra \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{{{\left( {a/2} \right)}^2}}} + \dfrac{1}{{{{\left( {a\sqrt 3 /2} \right)}^2}}} + \dfrac{1}{{{{\left( {a\sqrt 6 /4} \right)}^2}}} = \dfrac{8}{{{a^2}}} \Rightarrow OH = \dfrac{{a\sqrt 2 }}{4}\).
Tam giác \(OMH\) vuông tại \(H\) có \(OM = \dfrac{1}{2}SB = \dfrac{a}{2},OH = \dfrac{{a\sqrt 2 }}{4} \Rightarrow \sin \widehat {OMH} = \dfrac{{OH}}{{OM}} = \dfrac{{\sqrt 2 }}{2}\).
Vậy \(\sin \varphi = \dfrac{{\sqrt 2 }}{2}\).
Cho hình chóp S. ABC có đáy là tam giác ABC vuông cân tại A, cạnh SA vuông góc với mặt phẳng đáy, \(SA = \dfrac{{a\sqrt 6 }}{2},AB = a\). Gọi \(M\) là trung điểm của BC. Góc giữa đường thẳng SM và mặt phẳng \((ABC)\) có số đo bằng
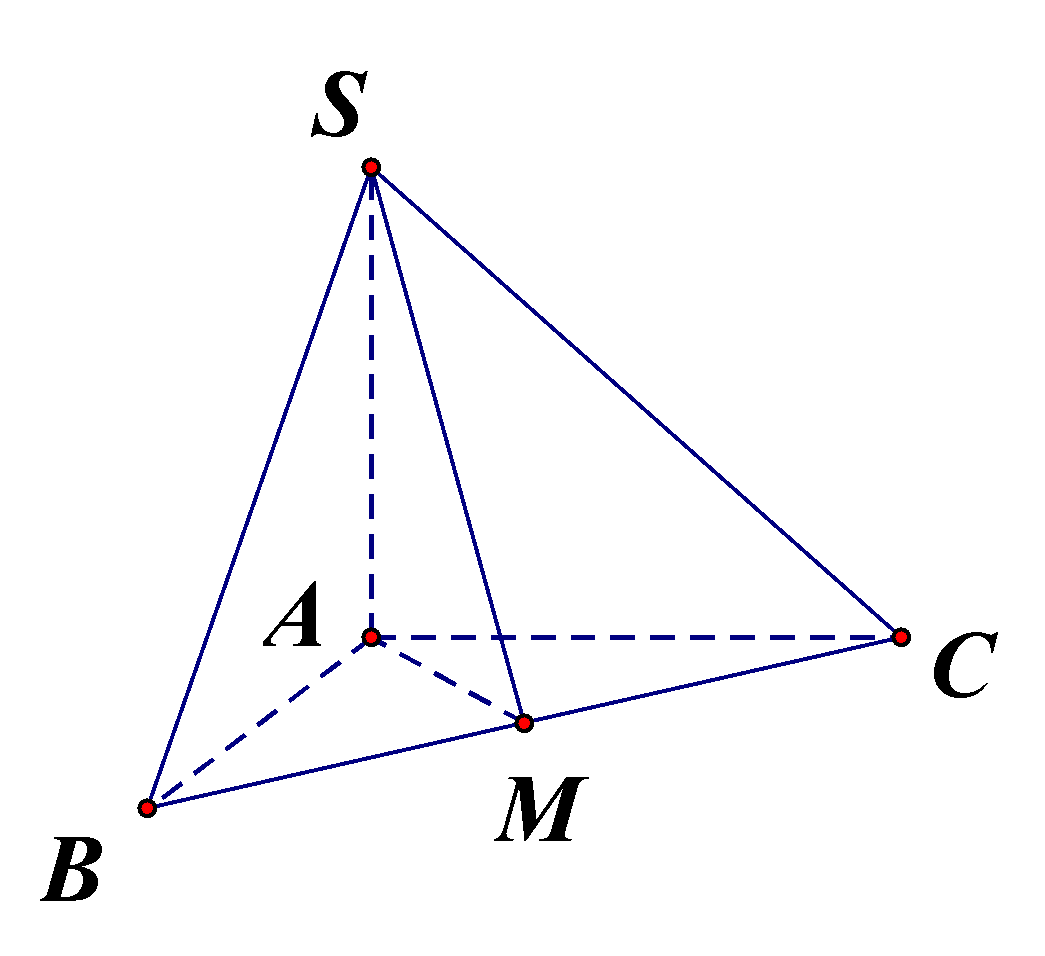
Bước 1: Xác định góc giữa SM và (ABC)
Do SM có hình chiếu vuông góc lên (ABC) là AM.
Do đó \(\widehat {\left( {SM,(ABC)} \right)} = \widehat {SMA}\).
Bước 2: Tính \(\widehat {SMA}\)
Ta có \(AM = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác vuông SAM có
\(\tan \widehat {SMA} = \dfrac{{SA}}{{AM}} = \dfrac{{\dfrac{{a\sqrt 6 }}{2}}}{{\dfrac{{a\sqrt 2 }}{2}}} = \sqrt 3 \)\( \Rightarrow \widehat {SMA} = {60^0}\)
Cho hình chóp S.ABCD có đáy là hình thoi tâm \(O\), tam giác ABD đều cạnh \(a\sqrt 2 .SA\) vuông góc với mặt phẳng đáy và \(SA = \dfrac{{3\sqrt 2 }}{2}a\). Hãy tính góc giữa đường thẳng SO và mặt phẳng \((ABCD)\).

Bước 1: Xác định góc giữa SO và đáy.
Ta có \(SA \bot (ABCD)\) nên AO là hình chiếu vuông góc của SO lên \((ABCD)\) nên góc giữa SO và đáy là góc \(\widehat {SOA}\).
Bước 2: Tính AO và \(\widehat {SOA}\)
Tam giác ABD đều cạnh \(a\sqrt 2 \) nên \(AO = a\sqrt 2 \dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{2}\).
Tam giác SAO vuông tại \(A\) nên ta có:
\(\tan \widehat {SOA} = \dfrac{{SA}}{{AO}} = \dfrac{{\dfrac{{3\sqrt 2 }}{2}a}}{{\dfrac{{a\sqrt 6 }}{2}}} = \sqrt 3 \)
Suy ra \(\widehat {SOA} = {60^0}\)
Vậy góc giữa đường thẳng SO và mặt phẳng \((ABCD)\) bằng \({60^0}\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a,SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Góc giữa đường thẳng SC và mặt phẳng \((ABCD)\) bằng
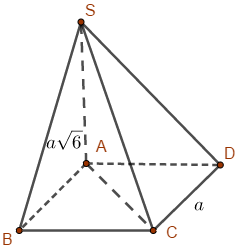
Bước 1:
Ta có \(SA \bot (ABCD)\) nên AC là hình chiếu của SC lên (ABCD). Vậy góc giữa SC và (ABCD) là góc giữa SC và AC và bằng \(\widehat {SCA}\)
Bước 2:
ABCD là hình vuông cạnh a nên \(AC = a\sqrt 2 \)
\(\begin{array}{l}\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 6 }}{{a\sqrt 2 }} = \sqrt 3 \\ \Rightarrow \widehat {SCA} = 60^\circ \end{array}\)
Cho hình chóp $S . A B C$ có đáy là tam giác vuông tại \(B\), cạnh bên $S A$ vuông góc với mặt phẳng đáy, \(AB = 2a,\widehat {BAC} = {60^0}\) và \(SA = a\sqrt 2 \). Góc giữa đường thẳng $S B$ và mặt phẳng \((SAC)\) bằng

Bước 1: Trong mặt phẳng \((ABC)\) kẻ \(BH \bot AC\). Xác định góc giữa đường thẳng SB và mặt phẳng \((SAC)\)
Trong mặt phẳng \((ABC)\) kẻ \(BH \bot AC\).
Mà \(BH \bot SA \Rightarrow BH \bot (SAC)\).
Góc giữa đường thẳng SB và mặt phẳng \((SAC)\) bằng \(\widehat {BSH}\).
Bước 2: Tính góc.
Xét tam giác ABH vuông tại \(H\) có
\(BH = AB \cdot \sin {60^0} = 2a \cdot \dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)
\(AH = AB \cdot \cos {60^0} = 2a \cdot \dfrac{1}{2} = a.\)
Xét tam giác SAH vuông tại $S$ có
\(SH = \sqrt {S{A^2} + A{H^2}} = \sqrt {{{(a\sqrt 2 )}^2} + {a^2}} = a\sqrt 3 .\)
Xét tam giác SBH vuông tại \(H\) có: \(SH = HB = a\sqrt 3 \), suy ra \(\Delta SBH\) vuông tại \(H\).
Vậy \(\widehat {BSH} = {45^0}\).
Đề thi THPT QG 2020 – mã đề 104
Cho hình chóp \(S.ABC\)có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a\); \(BC = a\sqrt 2 \); \(SA\) vuông góc với mặt phẳng đáy và \(SA = a\). Góc giữa đường thẳng \(SC\) và đáy bằng
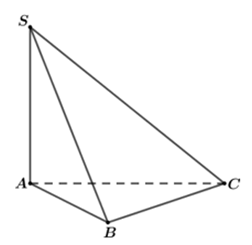
Ta có:\(SA \bot \left( {ABC} \right)\) \( \Rightarrow AC\) là hình chiếu của \(SC\) trên \(\left( {ABC} \right)\)
\( \Rightarrow \angle \left( {SC,\,\,\left( {ABC} \right)} \right) = \angle \left( {SC,\,\,AC} \right) = \angle SCA.\)
Áp dụng định lý Pitago cho \(\Delta SCA\) vuông tại \(A\) ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 .\)
\( \Rightarrow \tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}\) \( \Rightarrow \angle SCA = {30^0}.\)

