Dãy số

Thay \(n\) bằng \(n + 1\) trong công thức \({u_n}\) ta được: \({u_{n + 1}} = {2^{n + 1}} = {2.2^n}\).

Ta có \({u_n} = {3^n} \Rightarrow {u_{2n - 1}} = {3^{2n - 1}} = {3^n}{.3^{n - 1}}.\)

\({u_n} = {5^{n + 1}} \Rightarrow {u_{n - 1}} = {5^{\left( {n - 1} \right) + 1}} = {5^n}.\)

Cách 1: 

Phương án A:

${a_{n + 12}} = 2017\cos \dfrac{{\left[ {3(n + 12) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 1)\pi }}{6} + 6\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 1)\pi }}{6} = {a_n}.\forall n \ge 1.$

Phương án B: ${a_{n + 8}} = 2017\cos \dfrac{{\left[ {3(n + 8) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 1)\pi }}{6} + 4\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 1)\pi }}{6} = {a_n}.\forall n \ge 1.$

Phương án C: ${a_{n + 9}} = 2017\cos \dfrac{{\left[ {3(n + 9) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 4)\pi }}{6} + 4\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 4)\pi }}{6} \ne {a_n}.\forall n \ge 1.$

Phương án D:

${a_{n + 4}} = 2017\cos \dfrac{{\left[ {3(n + 4) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 1)\pi }}{6} + 2\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 1)\pi }}{6} = {a_n}.\forall n \ge 1.$

Cách 2: Sử dụng MTCT

Bước 1: Chuyển sang chế độ radian

Bước 2: Bấm 

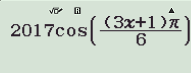
Bước 3: Sử dụng CALC và thay 

x=1 thì được $a_1=-\dfrac{2017}{2}$

$a_{n+12}=a_{13}=-\dfrac{2017}{2}$

$a_{n+8}=a_9=-\dfrac{2017}{2}$

$a_{n+9}=a_{10}\ne -\dfrac{2017}{2}$

$a_{n+4}=a_5=-\dfrac{2017}{2}$

Ta có ${a_n} = \dfrac{n}{{{n^2} + 100}} \le \dfrac{n}{{2\sqrt {{n^2}.100} }} = \dfrac{1}{{20}}.$

Dấu bằng xảy ra khi ${n^2} = 100 \Leftrightarrow n = 10.$

Vậy số hạng lớn nhất của dãy là số hạng bằng $\dfrac{1}{{20}}$.

Kiểm tra \({u_1} = 1\) ta loại đáp án A. Ta có \({u_2} = {u_1} + {1^2} = 2.\)

Xét đáp án B: ${u_n} = 1 + \dfrac{{n(n - 1)(2n + 2)}}{6} \Rightarrow {u_2} = 1 + \dfrac{{2.1.6}}{6} = 3\not  = 2 \Rightarrow $B loại.

Xét đáp án C: ${u_n} = {u_n} = 1 + \dfrac{{n(n - 1)(2n - 1)}}{6} \Rightarrow {u_2} = 1 + \dfrac{{2.1.3}}{6} = 2 \Rightarrow $Chọn C.

Xét đáp án D: ${u_n} = 1 + \dfrac{{n(n + 1)(2n - 2)}}{6} \Rightarrow {u_2} = 1 + \dfrac{{2.3.2}}{6} = 3\not  = 2 \Rightarrow $D loại.

Kiểm tra \({u_1} =  - 2\) ta loại các đáp án A, B. Ta có \({u_2} =  - 2 - \dfrac{1}{{{u_1}}} =  - \dfrac{3}{2}.\)

Xét đáp án C: ${u_n} =  - \dfrac{{n + 1}}{n} \Rightarrow {u_2} =  - \dfrac{3}{2} \Rightarrow $Chọn C.

Xét đáp án D. ${u_n} =  - \dfrac{n}{{n + 1}} \Rightarrow {u_2} =  - \dfrac{2}{3} \Rightarrow $D loại.

Ta có ${x_n} > 0,\forall n \ge 1$ và $\dfrac{1}{{{x_{n + 1}}}} = 2(2n + 1) + \dfrac{1}{{{x_n}}},\forall n \ge 1.$

\( \Rightarrow \dfrac{1}{{{x_{n + 1}}}} - \dfrac{1}{{{x_n}}} = 4n + 2\)

Ta có:

+) \(\dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_1}}} = 4.1 + 2\)

+) \(\dfrac{1}{{{x_3}}} - \dfrac{1}{{{x_2}}} = 4.2 + 2\)

…

+) \(\dfrac{1}{{{x_n}}} - \dfrac{1}{{{x_{n - 1}}}} = 4.\left( {n - 1} \right) + 2\)

Cộng vế với vế các đẳng thức trên được $\dfrac{1}{{{x_n}}} = \dfrac{1}{{{x_1}}} + 4(1 + 2 + ... + n - 1) + 2(n - 1)$$ = \dfrac{3}{2} + 2n(n - 1) + 2(n - 1) = \dfrac{{4{n^2} - 1}}{2}.$

Suy ra ${x_n} = \dfrac{2}{{4{n^2} - 1}}.$ Do đó ${x_{100}} = \dfrac{2}{{39999}}.$

Xét  đáp án C: \({u_n} = {2^n} \Rightarrow {u_{n + 1}} - {u_n} = {2^{n + 1}} - {2^n} = {2^n} > 0 \Rightarrow \) Chọn C.

Vì \({2^n};\,n\) là các dãy dương và tăng nên \(\dfrac{1}{{{2^n}}};\,\,\dfrac{1}{n}\) là các dãy giảm, do đó loại các đáp án A và B. 

Xét đáp án D: \({u_n} = {\left( { - 2} \right)^n} \Rightarrow \left\{ \begin{array}{l}{u_2} = 4\\{u_3} =  - 8\end{array} \right. \Rightarrow {u_2} > {u_3} \Rightarrow \) loại D.

Vì \({2^n}\) là dãy dương và tăng nên \(\dfrac{1}{{{2^n}}}\) là dãy giảm \( \Rightarrow \) Chọn A.

Xét B: ${u_n} = \dfrac{{3n - 1}}{{n + 1}} \Rightarrow \left\{ \begin{array}{l}{u_1} = 1\\{u_2} = \dfrac{5}{3}\end{array} \right. \Rightarrow {u_1} < {u_2} \Rightarrow $loại B. Hoặc

\({u_{n + 1}} - {u_n} = \dfrac{{3n + 2}}{{n + 2}} - \dfrac{{3n - 1}}{{n + 1}} = \dfrac{4}{{\left( {n + 1} \right)\left( {n + 2} \right)}} > 0\) nên \(\left( {{u_n}} \right)\) là dãy tăng.

Xét C: ${u_n} = {n^2} \Rightarrow {u_{n + 1}} - {u_n} = {\left( {n + 1} \right)^2} - {n^2} = 2n + 1 > 0 \Rightarrow $loại C.

Xét D: ${u_n} = \sqrt {n + 2}  \Rightarrow {u_{n + 1}} - {u_n} = \sqrt {n + 3}  - \sqrt {n + 2}  = \dfrac{1}{{\sqrt {n + 3}  + \sqrt {n + 2} }} > 0 \Rightarrow $loại D.

\({u_n} = \sin n \Rightarrow {u_{n + 1}} - {u_n} = 2\cos \left( {n + \dfrac{1}{2}} \right)\sin \dfrac{1}{2}\) có thể dương hoặc âm phụ thuộc \(n\) nên đáp án A sai. Hoặc dễ thấy \(\sin n\) có dấu thay đổi trên \({\mathbb{N}^*}\) nên dãy \(\sin n\) không tăng, không giảm.

\({u_n} = \dfrac{{{n^2} + 1}}{n} = n + \dfrac{1}{n} \Rightarrow {u_{n + 1}} - {u_n} = 1 + \dfrac{1}{{n + 1}} - \dfrac{1}{n} = \dfrac{{{n^2} + n - 1}}{{n\left( {n + 1} \right)}} > 0\) nên dãy đã cho tăng nên B sai.

\({u_n} = \sqrt n - \sqrt {n - 1} = \dfrac{1}{{\sqrt n  + \sqrt {n + 1} }},\) dãy \(\sqrt n  + \sqrt {n - 1}  > 0\) là dãy tăng nên suy ra \({u_n}\) giảm. Chọn C.

\({u_n} = {\left( { - 1} \right)^n}\left( {{2^n} + 1} \right)\) là dãy thay dấu nên không tăng không giảm.

+) Dãy số $({a_n})$ là dãy đan dấu nên không phải là dãy số tăng cũng không phải là dãy số giảm.

+) Dãy số $({b_n})$ là một dãy số tăng vì ${b_n} = n + \dfrac{1}{n} < n + 1 + \dfrac{1}{{n + 1}} = {b_{n + 1}},\forall n \ge 1.$

+) Dãy số $({c_n})$ là một dãy số giảm vì ${c_n} = \dfrac{1}{{{n^3} + 1}} > \dfrac{1}{{{{(n + 1)}^3} + 1}} = {c_{n + 1}},\forall n \ge 1.$

+) Dãy số $({d_n})$ là một dãy số tăng vì ${d_n} = {3.2^n} < {3.2^{n + 1}} = {d_{n + 1}},\forall n \ge 1.$

Vì \({2^n};\,n\) là các dãy dương và tăng nên \(\dfrac{1}{{{2^n}}};\,\,\dfrac{1}{n}\) là các dãy giảm, do đó loại các đáp án A và B.

Xét đáp án C: ${u_n} = \dfrac{{n + 5}}{{3n + 1}} \Rightarrow \left\{ \begin{array}{l}{u_1} = \dfrac{3}{2}\\{u_2} = \dfrac{7}{6}\end{array} \right. \Rightarrow {u_1} > {u_2} \Rightarrow $loại C.

Xét đáp án D: \({u_n} = \dfrac{{2n - 1}}{{n + 1}} = 2 - \dfrac{3}{{n + 1}} \Rightarrow {u_{n + 1}} - {u_n} = 3\left( {\dfrac{1}{{n + 1}} - \dfrac{1}{{n + 2}}} \right) > 0 \Rightarrow \)Chọn D.

Xét đáp án A: \({u_n} = \dfrac{1}{n} - 2 \Rightarrow {u_{n + 1}} - {u_n} = \dfrac{1}{{n + 1}} - \dfrac{1}{n} < 0 \Rightarrow \)loại A.

Xét đáp án B: \({u_n} = {\left( { - 1} \right)^n}\left( {{2^n} + 1} \right)\) là dãy có dấu thay đổi nên không giảm nên loại B.

Xét đáp án C: \({u_n} = \dfrac{{n - 1}}{{n + 1}} = 1 - \dfrac{2}{{n + 1}} \Rightarrow {u_{n + 1}} - {u_n} = 2\left( {\dfrac{1}{{n + 1}} - \dfrac{1}{{n + 2}}} \right) > 0 \Rightarrow \)loại C.

Xét đáp án D: \({u_n} = 2n + \cos \dfrac{1}{n} \Rightarrow {u_{n + 1}} - {u_n} = \left( {2 - \cos \dfrac{1}{{n + 1}}} \right) + \cos \dfrac{1}{{n + 2}} > 0\) nên Chọn D.

Xét A: \({u_n} = \dfrac{{1 - n}}{{\sqrt n }} = \dfrac{1}{{\sqrt n }} - \sqrt n \) \( \Rightarrow {u_{n + 1}} - {u_n} = \dfrac{1}{{\sqrt {n + 1} }} - \dfrac{1}{{\sqrt n }} + \sqrt n  - \sqrt {n + 1}  < 0\) nên dãy \(\left( {{u_n}} \right)\) là dãy giảm nên C đúng.

Xét đáp án B: \({u_n} = 2{n^2} - 5\) là dãy tăng vì \({n^2}\) là dãy tăng nên B đúng. Hoặc

\({u_{n + 1}} - {u_n} = 2\left( {2n + 1} \right) > 0\) nên \(\left( {{u_n}} \right)\) là dãy tăng.

Xét đáp án C: \({u_n} = {\left( {1 + \dfrac{1}{n}} \right)^n} = {\left( {\dfrac{{n + 1}}{n}} \right)^n} > 0 \Rightarrow \dfrac{{{u_{n + 1}}}}{{{u_n}}} = \dfrac{{n + 2}}{{n + 1}}.{\left( {\dfrac{{n + 2}}{n}} \right)^n} > 1 \Rightarrow \left( {{u_n}} \right)\) là dãy tăng nên Chọn C.

Xét đáp án D: \({u_n} = n + {\sin ^2}n \Rightarrow {u_{n + 1}} - {u_n} = \left( {1 - {{\sin }^2}\left( {n + 1} \right)} \right) + {\sin ^2}n > 0\) nên D đúng.

+) Dãy số $({a_n})$ là dãy số tăng và chỉ bị chặn dưới vì ${a_n} = \sqrt {{n^2} + 16}  \ge \sqrt {17} ,\forall n \ge 1.$

+) Dãy số $({b_n})$ là dãy số tăng và chỉ bị chặn dưới vì ${b_n} = n + \dfrac{1}{{2n}} > 2\sqrt {n.\dfrac{1}{{2n}}}  = \sqrt 2 ,\forall n \ge 1.$

+) Dãy số $({c_n})$ là dãy số tăng và chỉ bị chặn dưới vì ${c_n} = {2^n} + 3 \ge 5,\forall n \ge 1.$

+) Dãy số $({d_n})$ là dãy số bị chặn vì $0 < {d_n} \le \dfrac{1}{4},\forall n \ge 1.$ $\left( {do\,0 < \dfrac{n}{{{n^2} + 4}} \le \dfrac{n}{{4n}} = \dfrac{1}{4}} \right).$

+) Dãy số $({x_n})$ là dãy đan dấu và ${x_{2n}}$ lớn tùy ý khi $n$ đủ lớn, ${x_{2n + 1}}$ nhỏ tùy ý khi $n$ đủ lớn.

+) Dãy số $({y_n})$ là dãy số giảm và ${y_n}$ nhỏ tùy ý khi $n$ đủ lớn.

+) Dãy số $({z_n})$ là dãy số tăng nên nó bị chặn dưới bởi ${z_1} = \dfrac{{2018}}{{{{2017}^2}}}.$

+) Dãy số $({{\rm{w}}_n})$ là dãy đan dấu và ${{\rm{w}}_{2n}}$ lớn tùy ý khi $n$ đủ lớn, ${{\rm{w}}_{2n + 1}}$ nhỏ tùy ý khi $n$ đủ lớn.

Vì \({u_1} = {2.3^1} = 6\) nên ta loại các đáp án C và D. Ta có \({u_2} = {2.3^2} = 18.\)

Xét đáp án A: \(\left\{ \begin{array}{l}{u_1} = 6\\{u_n} = 6{u_{n - 1}},{\rm{ }}n > 1\end{array} \right. \Rightarrow {u_2} = 6{u_1} = 6.6 = 36 \Rightarrow \)A loại.

Xét đáp án B: \(\left\{ \begin{array}{l}{u_1} = 6\\{u_n} = 3{u_{n - 1}},{\rm{ }}n > 1\end{array} \right. \Rightarrow {u_2} = 3{u_1} = 3.6 = 18 \Rightarrow \)chọn B.

Ta có:

$\begin{array}{l}
{a_1} = 1\\
{a_2} = 2\\
{a_3} = \sqrt 3 {a_2} - {a_1} = 2\sqrt 3 - 1\\
{a_4} = \sqrt 3 {a_3} - {a_2} = \sqrt 3 \left( {2\sqrt 3 - 1} \right) - 2\\
= 6 - \sqrt 3 - 2 = 4 - \sqrt 3 \\
{a_5} = \sqrt 3 {a_4} - {a_3} = \sqrt 3 \left( {4 - \sqrt 3 } \right) - \left( {2\sqrt 3 - 1} \right)\\
= 4\sqrt 3 - 3 - 2\sqrt 3 + 1 = 2\sqrt 3 - 2\\
{a_6} = \sqrt 3 {a_5} - {a_4} = \sqrt 3 \left( {2\sqrt 3 - 2} \right) - \left( {4 - \sqrt 3 } \right)\\
= 2.3 - 2\sqrt 3 - 4 + \sqrt 3 = 2 - \sqrt 3 \\
{a_7} = \sqrt 3 {a_6} - {a_5} = \sqrt 3 \left( {2 - \sqrt 3 } \right) - \left( {2\sqrt 3 - 2} \right)\\
= 2\sqrt 3 - 3 - 2\sqrt 3 + 2 = - 1\\
{a_8} = \sqrt 3 {a_7} - {a_6} = \sqrt 3 .\left( { - 1} \right) - \left( {2 - \sqrt 3 } \right)\\
= - \sqrt 3 - 2 + \sqrt 3 = - 2\\
{a_9} = \sqrt 3 {a_8} - {a_7} = \sqrt 3 \left( { - 2} \right) - \left( { - 1} \right)\\
= - 2\sqrt 3 + 1\\
{a_{10}} = \sqrt 3 {a_9} - {a_8} = \sqrt 3 \left( { - 2\sqrt 3 + 1} \right) - \left( { - 2} \right)\\
= - 2.3 + \sqrt 3 + 2 = - 4 + \sqrt 3 \\
{a_{11}} = \sqrt 3 {a_{10}} - {a_9} = \sqrt 3 \left( { - 4 + \sqrt 3 } \right) - \left( { - 2\sqrt 3 + 1} \right)\\
= - 4\sqrt 3 + 3 + 2\sqrt 3 - 1 = - 2\sqrt 3 + 2\\
{a_{12}} = \sqrt 3 {a_{11}} - {a_{10}} = \sqrt 3 \left( { - 2\sqrt 3 + 2} \right) - \left( { - 4 + \sqrt 3 } \right)\\
= - 2.3 + 2\sqrt 3 + 4 - \sqrt 3 = - 2 + \sqrt 3 \\
{a_{13}} = \sqrt 3 {a_{12}} - {a_{11}} = \sqrt 3 \left( { - 2 + \sqrt 3 } \right) - \left( { - 2\sqrt 3 + 2} \right)\\
= - 2\sqrt 3 + 3 + 2\sqrt 3 - 2 = 1\\
{a_{14}} = \sqrt 3 {a_{13}} - {a_{12}} = \sqrt 3 .1 - \left( { - 2 + \sqrt 3 } \right)\\
= \sqrt 3 + 2 - \sqrt 3 = 2\\
\Rightarrow \left\{ \begin{array}{l}
{a_{13}} = {a_1}\\
{a_{14}} = {a_2}
\end{array} \right.
\end{array}$

Từ đây ta dự đoán được ${a_{n + 12}} = {a_n},\forall n \ge 1.$

Bằng phương pháp quy nạp toán học chúng ta chứng minh được ${a_{n + 12}} = {a_n},\forall n \ge 1.$

Vậy số nguyên dương cần tìm là $p = 12.$

+) Phương án A: Ta có ${a_1} = 1;{a_2} = \dfrac{{2018}}{{1 + 2017}} = 1;{a_3} = 1$. Từ đây ta dự đoán ${a_n} = 1,\forall n \ge 1.$

Bằng phương pháp quy nạp toán học, chúng ta chứng minh được rằng ${a_n} = 1,\forall n \ge 1.$

Suy ra $\left( {{a_n}} \right)$ là dãy số không đổi. Do đó phương án A đúng.

+) Phương án B: Ta có ${b_{n + 2}} = \tan \left[ {2(n + 2) + 1} \right]\dfrac{\pi }{4}$$ = \tan \left[ {(2n + 1)\dfrac{\pi }{4} + \pi } \right] = \tan (2n + 1)\dfrac{\pi }{4} = {b_n},\forall n \ge 1.$

Vậy ${b_{n + 2}} = {b_n},\forall n \ge 1.$ Do đó phương án B là đúng.

+) Phương án C: Ta có ${c_n} = 1,\forall n \ge 1$ nên dãy số $\left( {{c_n}} \right)$ là dãy số không đổi.

Suy ra $\left( {{c_n}} \right)$ là dãy số bị chặn. Do đó phương án C là đúng.

+) Phương án D: Ta có ${d_{2n}} = \cos (2n\pi ) = 1 = \cos (4n\pi ) = {d_{4n}}.$

Suy ra khẳng định $\left( {{d_n}} \right)$ là một dãy số giảm là khẳng định sai.