Cho dãy số $\left( {{a_n}} \right)$ xác định bởi ${a_n} = 2017\cos \dfrac{{\left( {3n + 1} \right)\pi }}{6}$. Mệnh đề nào dưới đây là sai 

Cách 1: 

Phương án A:

${a_{n + 12}} = 2017\cos \dfrac{{\left[ {3(n + 12) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 1)\pi }}{6} + 6\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 1)\pi }}{6} = {a_n}.\forall n \ge 1.$

Phương án B: ${a_{n + 8}} = 2017\cos \dfrac{{\left[ {3(n + 8) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 1)\pi }}{6} + 4\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 1)\pi }}{6} = {a_n}.\forall n \ge 1.$

Phương án C: ${a_{n + 9}} = 2017\cos \dfrac{{\left[ {3(n + 9) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 4)\pi }}{6} + 4\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 4)\pi }}{6} \ne {a_n}.\forall n \ge 1.$

Phương án D:

${a_{n + 4}} = 2017\cos \dfrac{{\left[ {3(n + 4) + 1} \right]\pi }}{6}$$ = 2017\cos \left( {\dfrac{{(3n + 1)\pi }}{6} + 2\pi } \right)$ $ = 2017\cos \dfrac{{(3n + 1)\pi }}{6} = {a_n}.\forall n \ge 1.$

Cách 2: Sử dụng MTCT

Bước 1: Chuyển sang chế độ radian

Bước 2: Bấm 

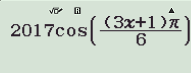
Bước 3: Sử dụng CALC và thay 

x=1 thì được $a_1=-\dfrac{2017}{2}$

$a_{n+12}=a_{13}=-\dfrac{2017}{2}$

$a_{n+8}=a_9=-\dfrac{2017}{2}$

$a_{n+9}=a_{10}\ne -\dfrac{2017}{2}$

$a_{n+4}=a_5=-\dfrac{2017}{2}$