Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác \(ABC\) được gọi là tam giác trung bình của tam giác \(ABC\).
Ta xây dựng dãy các tam giác \({A_1}{B_1}{C_1},{\rm{ }}{A_2}{B_2}{C_2},{\rm{ }}{A_3}{B_3}{C_3},...\) sao cho \({A_1}{B_1}{C_1}\) là một tam giác đều cạnh bằng \(3\) và với mỗi số nguyên dương \(n \ge 2\), tam giác \({A_n}{B_n}{C_n}\) là tam giác trung bình của tam giác \({A_{n - 1}}{B_{n - 1}}{C_{n - 1}}\). Với mỗi số nguyên dương \(n\), kí hiệu \({S_n}\) tương ứng là diện tích hình tròn ngoại tiếp tam giác \({A_n}{B_n}{C_n}\). Tính tổng \(S = {S_1} + {S_2} + ... + {S_n} + ...\)?
Tam giác \(ABC\) cạnh \(a\) thì có bán kính đường tròn ngoại tiếp là \(\dfrac{{a\sqrt 3 }}{3}\)
Với \(n = 1\) thì tam giác đều \({A_1}{B_1}{C_1}\) có cạnh bằng \(3\) nên đường tròn ngoại tiếp tam giác \({A_1}{B_1}{C_1}\)có bán kính \({R_1} = 3.\dfrac{{\sqrt 3 }}{3}\)\( \Rightarrow {S_1} = \pi {\left( {3.\dfrac{{\sqrt 3 }}{3}} \right)^2}\) .
Với \(n = 2\) thì tam giác đều \({A_2}{B_2}{C_2}\) có cạnh bằng \(\dfrac{3}{2}\) nên đường tròn ngoại tiếp tam giác \({A_2}{B_2}{C_2}\) có bán kính \({R_2} = 3.\dfrac{1}{2}.\dfrac{{\sqrt 3 }}{3}\)\( \Rightarrow {S_2} = \pi {\left( {3.\dfrac{1}{2}.\dfrac{{\sqrt 3 }}{3}} \right)^2}\) .
Với \(n = 3\) thì tam giác đều \({A_3}{B_3}{C_3}\) có cạnh bằng \(\dfrac{3}{4}\) nên đường tròn ngoại tiếp tam giác \({A_2}{B_2}{C_2}\) có bán kính \({R_3} = 3.\dfrac{1}{4}.\dfrac{{\sqrt 3 }}{3}\)\( \Rightarrow {S_3} = \pi {\left( {3.\dfrac{1}{4}.\dfrac{{\sqrt 3 }}{3}} \right)^2}\) .
...................
Như vậy tam giác đều \({A_n}{B_n}{C_n}\) có cạnh bằng \(3.{\left( {\dfrac{1}{2}} \right)^{n - 1}}\) nên đường tròn ngoại tiếp tam giác \({A_n}{B_n}{C_n}\) có bán kính \({R_n} = 3.{\left( {\dfrac{1}{2}} \right)^{n - 1}}.\dfrac{{\sqrt 3 }}{3}\)\( \Rightarrow {S_n} = \pi {\left( {3.{{\left( {\dfrac{1}{2}} \right)}^{n - 1}}.\dfrac{{\sqrt 3 }}{3}} \right)^2}\) .
Khi đó ta được dãy \({S_1}\), \({S_2}\), \(...{S_n}...\) là một cấp số nhân lùi vô hạn với số hạng đầu \({u_1} = {S_1} = 3\pi \) và công bội \(q = \dfrac{1}{4}\).
Do đó tổng \(S = {S_1} + {S_2} + ... + {S_n} + ...\)\( = \dfrac{{{u_1}}}{{1 - q}} = 4\pi \) .
Cho dãy số xác định bởi \({u_1} = 1\), \({u_{n + 1}} = \dfrac{1}{3}\left( {2{u_n} + \dfrac{{n - 1}}{{{n^2} + 3n + 2}}} \right);{\rm{ }}n \in {\mathbb{N}^*}\). Khi đó ${u_{2018}}$ bằng
Ta có: \({{\rm{u}}_{n + 1}} = \dfrac{1}{3}\left( {2{{\rm{u}}_n} + \dfrac{{n - 1}}{{{n^2} + 3n + 2}}} \right)\)\( = \dfrac{1}{3}\left( {2{u_n} + \dfrac{3}{{n + 2}} - \dfrac{2}{{n + 1}}} \right)\)\( = \dfrac{2}{3}{u_n} + \dfrac{1}{{n + 2}} - \dfrac{2}{3}.\dfrac{1}{{n + 1}}\).
$ \Leftrightarrow {u_{n + 1}} - \dfrac{1}{{n + 2}} = \dfrac{2}{3}\left( {{u_n} - \dfrac{1}{{n + 1}}} \right)$$\left( 1 \right)$
Đặt ${v_n} = {u_n} - \dfrac{1}{{n + 1}}$, từ $\left( 1 \right)$ta suy ra: ${v_{n + 1}} = \dfrac{2}{3}{v_n}$.
Do đó $\left( {{v_n}} \right)$ là cấp số nhân với ${v_1} = {u_1} - \dfrac{1}{2} = \dfrac{1}{2}$, công bội $q = \dfrac{2}{3}$.
Suy ra: ${v_n} = {v_1}.{q^{n - 1}} = \dfrac{1}{2}.{\left( {\dfrac{2}{3}} \right)^{n - 1}}$$ \Leftrightarrow {u_n} - \dfrac{1}{{n + 1}} = \dfrac{1}{2}.{\left( {\dfrac{2}{3}} \right)^{n - 1}}$$ \Leftrightarrow {u_n} = \dfrac{1}{2}.{\left( {\dfrac{2}{3}} \right)^{n - 1}} + \dfrac{1}{{n + 1}}$.
Vậy ${u_{2018}} = \dfrac{1}{2}.{\left( {\dfrac{2}{3}} \right)^{2017}} + \dfrac{1}{{2019}}$$ = \dfrac{{{2^{2016}}}}{{{3^{2017}}}} + \dfrac{1}{{2019}}$.
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi \({u_1} = 2\); \({u_n} = 2{u_{n - 1}} + 3n - 1\). Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng \(a{.2^n} + bn + c\), với \(a\), \(b\), \(c\) là các số nguyên, \(n \ge 2\); \(n \in \mathbb{N}\). Khi đó tổng \(a + b + c\) có giá trị bằng
Ta có \({u_n} = 2{u_{n - 1}} + 3n - 1\)\( \Leftrightarrow {u_n} + 3n + 5 = 2\left[ {{u_{n - 1}} + 3\left( {n - 1} \right) + 5} \right]\), với \(n \ge 2\); \(n \in \mathbb{N}\).
Đặt \({v_n} = {u_n} + 3n + 5\), ta có \({v_n} = 2{v_{n - 1}}\) với \(n \ge 2\); \(n \in \mathbb{N}\).
Như vậy, \(\left( {{v_n}} \right)\) là cấp số nhân với công bội \(q = 2\) và \({v_1} = 10\), do đó \({v_n} = {10.2^{n - 1}} = {5.2^n}\).
Do đó \({u_n} + 3n + 5 = {5.2^n}\), hay \({u_n} = {5.2^n} - 3n - 5\) với \(n \ge 2\); \(n \in \mathbb{N}\).
Suy ra \(a = 5\), \(b = - 3\), \(c = - 5\). Nên \(a + b + c = 5 + \left( { - 3} \right) + \left( { - 5} \right) = - 3\).
Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương anh A đều cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe?
Số tiền anh A cần tiết kiệm là \(500 - 500.0,32 = 340\) (triệu).
Gọi số tiền mà anh A nhận được ở mỗi tháng trong năm đầu tiên là \({u_1} = 10\) (triệu).
Thì số tiền mà anh A nhận được ở mỗi tháng trong năm thứ hai là
\({u_2} = {u_1}.\left( {1 + 0,12} \right) = {u_1}.1,12\) (triệu).
Số tiền mà anh \(A\) nhận được ở mỗi tháng trong năm thứ ba là
\({u_3} = {u_1}.{\left( {1 + 0,12} \right)^2} = {u_1}.{\left( {1,12} \right)^2}\) (triệu).
…
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ \(n\) là
\({u_n} = {u_1}.{\left( {1 + 0,12} \right)^{n - 1}}\)\( = {u_1}.{\left( {1,12} \right)^{n - 1}}\) (triệu).
Vậy số tiền mà anh A tiết kiệm được sau \(n\) năm là \(12.\left( {{u_2} - {u_1} + {u_3} - {u_2} + \cdot \cdot \cdot + {u_{n - 1}} - {u_{n - 2}} + {u_n} - {u_{n - 1}}} \right)\)\( = 12.\left( {{u_n} - {u_1}} \right)\)\( = 12.\left[ {{u_1}.{{\left( {1,12} \right)}^{n - 1}} - {u_1}} \right]\).
Cho \(12.\left[ {{u_1}.{{\left( {1,12} \right)}^{n - 1}} - {u_1}} \right] = 340\)
Thử từng đáp án \( \Rightarrow n = 13\).
Vậy sau ít nhất \(13\) năm thì anh A sẽ tiết kiệm đủ tiền để mua ô tô.
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\sqrt {u_1^2 + u_2^2 + 10} = \sqrt {2{u_1} + 6{u_2}} \) và \({u_{n + 2}} + {u_n} = 2{u_{n + 1}} + 1\) với mọi \(n \ge 1.\) Giá trị nhỏ nhất của \(n\) để \({u_n} > 5050\) bằng.
Ta có: \(\sqrt {u_1^2 + u_2^2 + 10} = \sqrt {2{u_1} + 6{u_2}} \)\( \Leftrightarrow u_1^2 + u_2^2 + 10 = 2{u_1} + 6{u_2}\)
\( \Leftrightarrow {\left( {{u_1} - 1} \right)^2} + {\left( {{u_2} - 3} \right)^2} = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 1\\{u_2} = 3\end{array} \right.\).
Đặt \({v_n} = {u_{n + 1}} - {u_n}\) với \(n \ge 1\)\( \Rightarrow {v_1} = {u_2} - {u_1} = 2\).
Theo giả thiết: \({u_{n + 2}} + {u_n} = 2{u_{n + 1}} + 1\)\( \Leftrightarrow {u_{n + 2}} - {u_{n + 1}} = {u_{n + 1}} - {u_n} + 1 \Leftrightarrow {v_{n + 1}} = {v_n} + 1\), \(\forall n \ge 1\).
Suy ra \(\left( {{v_n}} \right)\) là cấp số cộng có công sai \(d = 1\)\( \Rightarrow {v_n} = {v_1} + \left( {n - 1} \right)d = 2+n-1=n+1\).
Ta có: \({u_{n + 1}} = \underbrace {{u_{n + 1}} - {u_n}}_{{v_n}} + \underbrace {{u_n} - {u_{n - 1}}}_{{v_{n - 1}}} + ... + \underbrace {{u_3} - {u_2}}_{{v_2}} + \underbrace {{u_2} - {u_1}}_{{v_1}} + {u_1} \) \(= {S_n} + {u_1}\).
Với \({S_n} = {v_1} + {v_2} + ... + {v_n} = \dfrac{n}{2}\left( {{v_1} + {v_n}} \right) = \dfrac{{n\left( {n +3} \right)}}{2}\).
Suy ra: \({u_{n + 1}} = \dfrac{{n\left( {n +3 } \right)}}{2} + 1 \) \(\Rightarrow {u_n} = \dfrac{{\left( {n - 1} \right)\left( {n + 2} \right)}}{2} + 1\).
Ta có: ${u_n} > 5050 \Leftrightarrow \dfrac{{\left( {n - 1} \right)\left( {n + 2} \right)}}{2} + 1 > 5050 $ $\Leftrightarrow {n^2} +n - 10100 > 0 \Leftrightarrow n > 100$.
Vậy số \(n\) nhỏ nhất thỏa yêu cầu là \(101\).
Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có $10$ tầng thì bạn An cần đúng bao nhiêu que diêm?
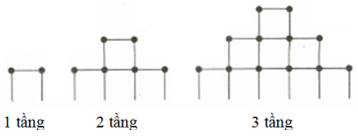
Số que ở $1$ tầng là ${u_1} = 3$.
Tổng số que ở $2$ tầng là ${u_1} + {u_2} = 3 + 7$.
Tổng số que ở $3$ tầng là ${u_1} + {u_2} + {u_3} = 3 + 7 + 11$.
.
Ta có cấp số cộng ${u_1} = 3$, $d = 4$, tính ${S_{10}}$?
Để cần có $10$ tầng cần tổng ${S_{10}} = \dfrac{{10}}{2}\left( {2.3 + 9.4} \right) = 210$ que.
Cho $a < b < c$ là ba số nguyên. Biết $a$, $b$, $c$ theo thứ tự tạo thành một cấp số cộng và $a$, $c$, $b$ theo thứ tự tạo thành một cấp số nhân. Tìm giá trị nhỏ nhất của $c$.
Ta có \(\left\{ {\begin{array}{*{20}{c}}{2b = a + c}\\{{c^2} = ab > 0}\end{array}} \right.\). Suy ra: \(2{c^2} = a\left( {a + c} \right) \Rightarrow 2{c^2} - ac - {a^2} = 0 \Rightarrow \left[ \begin{array}{l}c = a\left( L \right)\\c = - \dfrac{a}{2} \Rightarrow b = \dfrac{a}{4} = - \dfrac{c}{2}\end{array} \right.\).
Suy ra \(a\), \(b\) trái dấu với \(c\) \( \Rightarrow \left\{ \begin{array}{l}a < 0\\c > 0\end{array} \right.\).
Do \(a\), \(b\), \(c\) nguyên nên \(c\) chia hết cho \(2\).
Do đó \(c\) nhỏ nhất bằng \(2\) khi đó \(a = - 4\), \(b = - 1\) (thỏa mãn).
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = \sqrt 2 \) và \({u_{n + 1}} = \sqrt {2 + {u_n}} \) với mọi \(n \ge 1\). Tìm \({u_{2018}}\).
Ta có:
\({u_1} = \sqrt 2 = 2\cos \dfrac{\pi }{4} = 2\cos \dfrac{\pi }{{{2^2}}}\).
\({u_2} = \sqrt {2 + \sqrt 2 } = 2\cos \dfrac{\pi }{8} = 2\cos \dfrac{\pi }{{{2^3}}}\).
Dự đoán: ${u_n} = 2\cos \dfrac{\pi }{{{2^{n + 1}}}}$.
Chứng minh theo quy nạp ta có:
${u_1} = 2\cos \dfrac{\pi }{4} = \sqrt 2 $, công thức $\left( 1 \right)$ đúng với $n = 1$.
Giả sử công thức $\left( 1 \right)$ đúng với $n = k$, \(k \ge 1\) ta có ${u_k} = 2\cos \dfrac{\pi }{{{2^{k + 1}}}}$.
Ta có: ${u_{k + 1}} = \sqrt {2 + {u_k}} = \sqrt {2 + 2\cos \dfrac{\pi }{{{2^{k + 1}}}}} = \sqrt {2\left( {1 + \cos \dfrac{\pi }{{{2^{k + 1}}}}} \right)} = \sqrt {4{{\cos }^2}\left( {\dfrac{\pi }{{{2^{k + 2}}}}} \right)} = 2\cos \dfrac{\pi }{{{2^{k + 2}}}}$
(vì \(0 < \dfrac{\pi }{{{2^{k + 2}}}} < \dfrac{\pi }{2}\) với mọi \(k \ge 1\)).
Công thức $\left( 1 \right)$ đúng với $n = k + 1$.
Vậy ${u_n} = 2\cos \dfrac{\pi }{{{2^{n + 1}}}}$, $\forall n \in N$. Suy ra \({u_{2018}} = 2\cos \dfrac{\pi }{{{2^{2019}}}}\).
Cho dãy số $\left( {{u_n}} \right)$ thỏa mãn $\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \dfrac{{{u_n} + \sqrt 2 - 1}}{{1 - \left( {\sqrt 2 - 1} \right){u_n}}}\end{array} \right.$, $\forall n \in {\mathbb{N}^*}$. Tính ${u_{2018}}$.
Đặt ${u_1} = \tan \alpha = 2$. Ta có $\tan \dfrac{\pi }{8} = \sqrt 2 - 1$. Suy ra ${u_{n + 1}} = \dfrac{{{u_n} + \tan \dfrac{\pi }{8}}}{{1 - \tan \dfrac{\pi }{8}.{u_n}}}$
Có ${u_2}$$ = \dfrac{{\tan \alpha + \tan \dfrac{\pi }{8}}}{{1 - \tan \dfrac{\pi }{8}.\tan {u_n}}} = \tan \left( {\alpha + \dfrac{\pi }{8}} \right)$.
Bằng quy nạp, ta chứng minh được ${u_n} = \tan \left[ {\alpha + \left( {n - 1} \right)\dfrac{\pi }{8}} \right]$.
Vậy ${u_{2018}} = \tan \left( {\alpha + \dfrac{{2017\pi }}{8}} \right) = \tan \left( {\alpha + \dfrac{\pi }{8}} \right) = \dfrac{{\tan \alpha + \tan \dfrac{\pi }{8}}}{{1 - \tan \alpha .\tan \dfrac{\pi }{8}}} = 7 + 5\sqrt 2 $.
Có hai cơ sở khoan giếng A và B. Cơ sở A giá mét khoan đầu tiên là \(8000\) (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm \(500\) (đồng) so với giá của mét khoan ngay trước đó. Cơ sở B: Giá của mét khoan đầu tiên là \(6000\) (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm \(7\% \) giá của mét khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần lượt là \(20\)$\left( {\rm{m}} \right)$ và \(25\)$\left( {\rm{m}} \right)$ để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất?
Cơ sở \(A\) giá mét khoan đầu tiên là \(8000\) (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm \(500\) (đồng) so với giá của mét khoan ngay trước đó. Do đó theo tổng của một cấp số cộng ta có:
+ Nếu đào giếng \(20\) $\left( {\rm{m}} \right)$ hết số tiền là: \({S_{20}} = \dfrac{{20}}{2}\left[ {2.8000 + \left( {20 - 1} \right)500} \right] = 255000\) (đồng).
+ Nếu đào giếng \(25\) $\left( {\rm{m}} \right)$ hết số tiền là: \({S_{25}} = \dfrac{{25}}{2}\left[ {2.8000 + \left( {25 - 1} \right)500} \right] = 350000\) (đồng).
Cơ sở \(B\) giá của mét khoan đầu tiên là \(6000\) (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm \(7\% \) giá của mét khoan ngay trước đó. Do đó theo tổng của một cấp số nhân ta có:
+ Nếu đào giếng \(20\) $\left( {\rm{m}} \right)$ hết số tiền là: \(S{'_{20}} = 6000\dfrac{{1 - {{\left( {1,07} \right)}^{20}}}}{{1 - 1,07}} \approx 245973\) (đồng).
+ Nếu đào giếng \(25\) $\left( {\rm{m}} \right)$ hết số tiền là: \({S'_{25}} = 6000\dfrac{{1 - {{\left( {1,07} \right)}^{25}}}}{{1 - 1,07}} \approx 379494\) (đồng).
Ta thấy \({S'_{20}} < {S_{20}}\), \({S'_{25}} > {S_{25}}\) nên giếng \(20\)$\left( {\rm{m}} \right)$ chọn B còn giếng \(25\)$\left( {\rm{m}} \right)$ chọn A.
