Trong mặt phẳng cho 2019 điểm phân biệt. Hỏi có tất cả bao nhiêu vectơ khác vectơ không mà có điểm đầu và điểm cuối thuộc 2019 điểm trên?
Bước 1:
Cứ 2 điểm bất kì trong 2019 điểm đã cho sẽ tạo thành 2 véctơ khác véctơ không.
Bước 2:
Số cách chọn 2 điểm trong 2019 điểm phân biệt là \(C_{2019}^2\).
Bước 3:
Theo quy tắc nhân ta có tất cả số véctơ là: \(2.C_{2019}^2 = 2.\dfrac{{2019!}}{{2!.2017!}} = \dfrac{{2019!}}{{2017!}}\)
Có \(2\) học sinh lớp A, \(3\) học sinh lớp B và \(4\) học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh lớp B. Hỏi có bao nhiêu cách xếp hàng như vậy?
Xếp 2 học sinh lớp A có \(2!\) cách xếp, khi đó tạo ra 3 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ nhất vào 1 trong 2 khoảng trống không ở giữa 2 bạn lớp A có 2 cách, khi đó tạo ra 4 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ 2 vào 1 trong 3 khoảng trống không ở giữa 2 bạn lớp A có 3 cách, khi đó tạo ra 5 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ 3 vào 1 trong 4 khoảng trống không ở giữa 2 bạn lớp A có 4 cách, khi đó tạo ra 6 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp C thứ nhất vào 1 trong 6 khoảng trống (kể cả khoảng trống giữa 2 bạn lớp A) có 6 cách, khi đó tạo ra 7 khoảng trống.
Cứ như vậy ta có :
Xếp bạn lớp C thứ hai có 7 cách.
Xếp bạn lớp C thứ ba có 8 cách.
Xếp bạn lớp C thứ tư có 9 cách.
Vậy số cách xếp 9 học sinh trên thỏa mãn yêu cầu là \(2!.2.3.4.6.7.8.9 = 145152\) cách.
Có 5 cuốn sách toán khác nhau và 5 cuốn sách văn khác nhau. Có bao nhiêu cách sắp xếp chúng thành 1 hàng sao cho các cuốn sách cùng môn thì đứng kề nhau ?
Bước 1:
Ta có số cách sắp xếp 5 cuốn sách toán khác nhau là 5!
Bước 2:
Số cách sắp xếp 5 cuốn sách văn khác nhau là 5!
Bước 3:
Có 2 cách để sắp xếp 5 cuốn sách toán khác nhau và 5 cuốn sách văn khác nhau thành 1 hàng ngang.
Bước 4:
Theo quy tắc nhân ta có số cách xếp thỏa mãn bài toán là 2.5!.5!
Có bao nhiêu số tự nhiên có \(4\) chữ số đôi một khác nhau không vượt quá \(2020?\)
Gọi số cần tìm là \(\overline {abcd} \left( {a \ne 0,0 \le a,b,c,d \le 9,a,b,c,d \in N} \right)\)
Theo bài ra ta có \(\overline {abcd} \le 2020\)
+) TH1 : \(a = 1\)
\(b\) có 9 cách chọn
\(c\) có 8 cách chọn
\(d\) có 7 cách chọn
Nên có \(9.8.7 = 504\) số
+)TH2 : \(a = 2\) suy ra \(b = 0\), \(c = 1\) và \(d\) có \(7\) cách chọn
Nên có \(7\) số thỏa mãn.
Vậy có tất cả \(504 + 7 = 511\) số.
Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) sao cho số đó chia hết cho \(15\)?
Gọi số tự nhiên cần lập có dạng \(\overline {abcd} \;\;\;\left( {a,\;b,\;c,\;d \in \left\{ {1;\;2;\;3;\;4;\;5;\;6;\;7;\;8;\;9} \right\}} \right).\)
Số cần lập chia hết cho 15 nên nó chia hết cho 3 và 5.
Số cần lập chia hết cho 5 nên ta có: \(d = 5 \Rightarrow d\) có 1 cách chọn.
\( \Rightarrow \) Số cần tìm có dạng: \(\overline {abc5} .\)
Số cần lập chia hết cho 3 nên \(\left( {a + b + c + 5} \right)\; \vdots \;3.\)
Chọn \(a\) có 9 cách chọn, chọn \(b\) có 9 cách chọn.
+) Nếu \(\left( {a + b + 5} \right)\; \vdots \;3 \Rightarrow c \in \left\{ {3;\;6;\;9} \right\} \Rightarrow c\) có 3 cách chọn.
+) Nếu \(\left( {a + b + 5} \right)\) chia cho \(3\) dư \(1 \Rightarrow c \in \left\{ {2;\;5;\;8} \right\} \Rightarrow c\) có 3 cách chọn.
+) Nếu \(\left( {a + b + 5} \right)\) chia cho \(2\) dư \(2 \Rightarrow c \in \left\{ {1;\;4;\;7} \right\} \Rightarrow c\) có 3 cách chọn.
\( \Rightarrow \) Có 3 cách chọn \(c.\)
Như vậy có: \(9.9.3.1 = 243\) cách chọn.
Vậy có 243 số thỏa mãn yêu cầu bài toán.
Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số khác nhau?
Giả sử số tự nhiên chẵn gồm 3 chữ số khác nhau là: \(\overline {abc} \,\,\left( {a \ne 0} \right)\)
Khi đó, \(c \in \left\{ {0;2;4;6;8} \right\}\)
+) Nếu \(c = 0\) có 1 cách chọn
\(a\) có 9 cách chọn
\(b\) có 8 cách chọn
\( \Rightarrow \) Có: \(1.9.8 = 72\) (số)
+) Nếu \(c \in \left\{ {2;4;6;8} \right\}\) có 4 cách chọn
\(a\) có 8 cách chọn
\(b\) có 8 cách chọn
\( \Rightarrow \) Có: \(4.8.8 = 256\) (số)
Vậy, số số tự nhiên chẵn gồm 3 chữ số khác nhau là: \(72 + 256 = 328\)(số).
Cho hai tập hợp$A = \{ a,b,c,d\} $ ;$B = \{ c,d,e\} $. Chọn khẳng định sai trong các khẳng định sau:
Ta có : \(A \cup B = \left\{ {a,b,c,d,e} \right\} \Rightarrow N\left( {A \cup B} \right) = 5\)
Trong một trò chơi của chương trình truyền hình thực tế RNM, có hai đội chơi chia như sau:
+ Đội 1 gồm các thành viên: KJK, YSC, HH, SJH, KGR.
+ Đội 2 gồm các thành niên: YJS, JSJ, JSM, LKS.
Kết thúc trò chơi, cả hai đội đều chưa hoàn thành nhiệm vụ, cần chọn ra ngẫu nhiên \(1\) thành viên thuộc \(1\) trong \(2\) đội để nhận hình phạt. Biết rằng khả năng bị chọn trúng của mỗi người là như nhau. Hỏi có tất cả bao nhiêu cách chọn người bị phạt?
Có hai khả năng chọn người bị phạt: đó là chọn phải người ở đội 1 hoặc chọn phải người ở đội 2.
- Chọn người bị phạt ở đội 1 thì có \(5\) cách.
- Chọn người bị phạt ở đội 2 thì có \(4\) cách.
Vậy có tất cả \(5 + 4 = 9\) cách chọn.
Một lớp có \(3\) tổ được chia như sau: Đội \(1\) có \(12\) người, đội \(2\) có \(11\) người, đội \(3\) có \(13\) người. Giáo viên cần chọn ra \(1\) bạn làm lớp trưởng, biết rằng giáo viên chỉ chọn một ở tổ \(1\) hoặc \(3\) làm lớp trưởng, còn các bạn ở tổ \(2\) thì chọn lấy \(1\) bạn làm lớp phó học tập. Hỏi có bao nhiêu cách chọn ra lớp trưởng?
Có hai khả năng để giáo viên chọn:
+) Tổ 1 có bạn được làm lớp trưởng thì có \(12\) cách chọn.
+) Tổ 3 có bạn được chọn làm lớp trưởng thì có \(13\) cách chọn.
Vậy có tất cả \(12 + 13 = 25\) cách chọn.
Từ thành phố A đến thành phố B có $3$ con đường, từ thành phố A đến thành phố C có $2$ con đường, từ thành phố B đến thành phố D có $2$ con đường, từ thành phố C đến thành phố D có $3$ con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
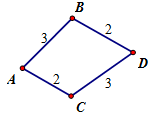
Số cách đi từ A đến D bằng cách đi từ A đến B rồi đến D là \(3.2 = 6\).
Số cách đi từ A đến D bằng cách đi từ A đến C rồi đến D là \(2.3 = 6\).
Nên có : \(6 + 6 = 12\) cách.
Số điện thoại ở Huyện Củ Chi có $7$ chữ số và bắt đầu bởi $3$ chữ số đầu tiên là $790$. Hỏi ở Huyện Củ Chi có tối đa bao nhiêu máy điện thoại:
Gọi số điện thoại cần tìm có dạng \(\overline {790abcd} \).
Khi đó: \(a\)có 10 cách chọn, \(b\)có 10 cách chọn, \(c\)có 10 cách chọn, \(d\) có 10 cách chọn.
Nên có tất cả \(10.10.10.10 = {10^4}\) số.
Có bao nhiêu số tự nhiên gồm $5$ chữ số, các chữ số đều lớn hơn $4$ và đôi một khác nhau:
Gọi số tự nhiên cần tìm có dạng \(\overline {abcde} \).
Các số $a,b,c,d,e$ thuộc tập hợp $\left\{5;6;7;8;9\right\}$
Khi đó: \(a\) có 5 cách chọn, \(b\) có 4 cách chọn, \(c\) có 3 cách chọn, \(d\) có 2 cách chọn, \(e\) có 1 cách chọn.
Nên có tất cả \(5.4.3.2.1 = 120\) số.
Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có $8$ màu khác nhau, các cây bút chì cũng có $8$ màu khác nhau. Như vậy bạn có bao nhiêu cách chọn
Chọn cây bút mực: có $8$ cách
Chọn cây bút chì: có $8$ cách
Theo quy tắc nhân, số cách mua là: $8.8 = 64$ (cách)
Có bao nhiêu cách xếp \(5\) sách Văn khác nhau và \(7\) sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
Bước 1:
Coi 5 quyển sách Văn chỉ xếp vào 1 chỗ.
Bước 2:
Như vậy ta sẽ xếp \(5\) quyển sách Văn và \(7\) quyển sách Toán vào \(8\) vị trí trên kệ sách.
Bước 3:
Số cách xếp 5 quyển sách Văn là \(5!\)
Bước 4:
Số cách xếp xếp \(5\) quyển sách Văn và \(7\) quyển sách Toán trên kệ sách dài sao cho \(5\) quyển sách Văn xếp kề nhau là \(5!.8!\) cách.
Có bao nhiêu cách sắp xếp $3$ nữ sinh, $3$ nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẻ:
Chọn vị trí cho hai nhóm $3$ nam và $3$ nữ có \(2\) cách chọn (1 nhóm ở vị trí chẵn và nhóm còn lại ở vị trí lẻ)
Xếp 3 nam có: \(3.2.1\) cách xếp.
Xếp 3 nữ có: \(3.2.1\) cách xếp.
Vậy có \(2.{\left( {3.2.1} \right)^2} = 72\) cách xếp.
Cho các số $1,2,3,4,5,6,7$. Số các số tự nhiên gồm $5$ chữ số lấy từ $7$ chữ số trên sao cho chữ số đầu tiên bằng $3$ là:
Gọi số cần tìm có dạng : \(\overline {abcde} \).
Chọn \(a\) : có 1 cách \(\left( {a = 3} \right)\)
Chọn \(\overline {bcde} \) : có \({7^4}\) cách
Theo quy tắc nhân, có \({1.7^4} = 2401\) (số)
Trên giá sách có $6$ quyển Văn khác nhau, $5$ quyển sách Toán khác nhau và $9$ quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?
Theo quy tắc nhân ta có:
$6.5 = 30$ cách chọn một quyển Văn và một quyển Toán khác nhau.
$6.9 = 54$ cách chọn một quyển Văn và một quyển Tiếng Anh khác nhau.
$5.9 = 45$ cách chọn một quyển Toán và một quyển Tiếng Anh khác nhau.
Theo quy tắc cộng ta có số cách chọn hai quyển sách khác môn là: $30 + 54 + 45 = 129$ cách.
Sắp xếp \(5\) học sinh lớp \(A\) và \(5\) học sinh lớp \(B\) vào hai dãy ghế đối diện nhau, mỗi dãy \(5\) ghế sao cho \(2\) học sinh ngồi đối diện nhau thì khác lớp. Khi đó số cách xếp là:
Cách 1:
Bước 1: Học sinh đầu tiên, giả sử đó là học sinh lớp $A$ có $10$ cách chọn ghế.
Bước 2: Khi đó ta cần chọn một bạn lớp B để xếp vào vị trí đối diện của bạn lớp A vừa rồi, suy ra có $5$ cách chọn.
Bước 3: Còn trống $8$ ghế nên có $8$ cách xếp học sinh thứ 2 của lớp $A$.
Bước 4: Có $4$ cách chọn ra học sinh lớp $B$ vào ghế đối diện bạn vừa được sắp xếp (bạn lớp A).
Bước 5: Có $6$ cách xếp học sinh thứ 3 của lớp $A$.
Bước 6: Có $3$ cách chọn học sinh lớp $B$ vào ghế đối diện.
Bước 7: Có $4$ cách xếp học sinh thứ 4 của lớp $A$ vào ghế tiếp.
Bước 8: Có $2$ cách chọn học sinh lớp $B$ vào ghế đối diện.
Bước 9: Có $2$ cách xếp học sinh cuối cùng của lớp $A$ vào ghế kế tiếp.
Bước 10: Có $1$ cách chọn học sinh lớp $B$ vào ghế đối diện.
Theo quy tắc nhân thì có $10.5.8.4.6.3.4.2.2.1 = {\left( {5!} \right)^2}{.2^5} = 460800$ cách.
Cách 2:
Vì $2$ học sinh ngồi đối diện nhau thì khác lớp nên mỗi cặp ghế đối diện nhau sẽ được xếp bởi $1$ học sinh lớp $A$ và $1$ học sinh lớp $B$.
Số cách xếp $5$ học sinh lớp $A$ vào $5$ cặp ghế là $5!$ cách. Số cách xếp $5$ học sinh lớp $B$ vào $5$ cặp ghế là $5!$ cách. Số cách xếp chỗ ở mỗi cặp ghế là $2$ cách.
Theo quy tắc nhân thì có ${\left( {5!} \right)^2}{.2^5} = 460800$ cách.
Xếp \(6\) người (trong đó có một cặp vợ chồng) ngồi quanh bàn tròn có \(6\) cái ghế không ghi số sao cho cặp vợ chồng ngồi cạnh nhau. Số cách xếp là:
Áp dụng quy tắc “buộc” các phần tử ta có \(2!\) cách xếp hai vợ chồng.
Sau khi “buộc” hai vợ chồng lại thì ta có tất cả $5$ phần tử.
Theo công thức hoán vị vòng quanh thì số cách xếp $5$ phần tử quanh bàn tròn là \(4!\).
Vậy theo quy tắc nhân thì có \(2!.4! = 48\).
Cho \(X = \left\{ {0,1,2,3,4,5,6,7} \right\}\). Có thể lập được bao nhiêu số tự nhiên có $5$ chữ số khác nhau đôi một từ X sao cho một trong $3$ chữ số đầu tiên phải có mặt chữ số $1$.
Gọi số tự nhiên cần tìm là \(\overline {abcde} \,\,\left( {a \ne 0} \right)\)
TH1: Nếu $a = 1$ khi đó:
Có $1$ cách chọn $a$.
Có $7$ cách chọn $b$.
Có $6$ cách chọn $c$.
Có $5$ cách chọn $d.$
Có $4$ cách chọn $e$.
Áp dụng quy tắc nhân ta có: $1.7.6.5.4 = 840$ số.
TH2: Nếu \(a \ne 1\) khi đó:
Có 6 cách chọn a.
Có 2 cách xếp vị trí cho chữ số 1 là b hoặc c.
Cách xếp các chữ số còn lại có 6.5.4 = 120 cách.
Áp dụng quy tắc nhân ta có: 6.2.120 = 1440 số.
Vậy theo quy tắc cộng ta có: 840 + 1440 = 2280 số.

