Tổng hợp câu hay và khó chương 8 phần 1

Do tứ diện $MNPQ$ đều nên ta có $MN \bot PQ$ hay $EC' \bot BF$.

Ta có: $\overrightarrow {B'F}  = \overrightarrow {B'A}  + \overrightarrow {AF}  = \overrightarrow {B'A'}  + \overrightarrow {B'B}  + k\overrightarrow {AD}  = \overrightarrow {B'A'}  + \overrightarrow {B'B}  + k\overrightarrow {B'C'}$

Và $\overrightarrow {EC'}  = \overrightarrow {EC}  + \overrightarrow {CC'}  = \dfrac{1}{2}\overrightarrow {B'C'}  - \overrightarrow {B'B}$

Khi đó, $\overrightarrow {EC'} .\overrightarrow {BF}  =  - B'{B^2} + \dfrac{k}{2}B'{C'^2} =  - 4 + \dfrac{k}{2}.4 = 0$$\Rightarrow k = 2$. Vậy $\overrightarrow {AF}  = 2\overrightarrow {AD}$

Vậy $F$ là điểm trên $AD$ sao $D$ là trung điểm của $AF$.

Do đó $DF = BC = 2{\rm{cm}}$.

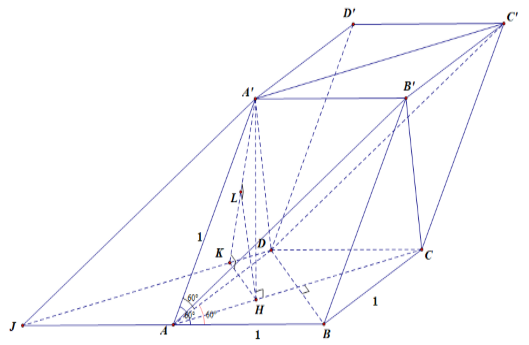
Ta có $\widehat {BAA'\,} = \widehat {DAA'}$$= \widehat {BAD} = 60^\circ$ và $AB = AD$$= AA' = 1$.

Khi đó $\Delta ABD$, $\Delta ADA'$ và $\Delta ABA'$ đều cạnh bằng $1$.

$\Rightarrow A'D = A'A$$= A'B = 1$. Suy ra hình chiếu của $A'$ lên $\left( {ABCD} \right)$ là tâm H của $\Delta ABD$ đều.

Ta có $AB'\;{\rm{//}}\;DC'$$\Rightarrow d\left( {AB';A'C'} \right) = d\left( {AB';\left( {DA'C'} \right)} \right)$$= d\left( {H;\left( {DA'C'} \right)} \right)$.

Dựng hình bình hành $DCAJ$. Từ $H$ kẻ $HK \bot DJ$$\left( {K \in DJ} \right)$, ta có $HK\;{\rm{//}}\;DB$.

Từ $H$ kẻ $HL \bot A'K$$\left( {L \in A'K} \right)$$\Rightarrow HL \bot \left( {DA'C'} \right)$$\Rightarrow d\left( {H;\left( {DA'C'} \right)} \right) = HL$.

Ta có: $HK = \dfrac{1}{2}$, $A'H = \sqrt {1 - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{\sqrt 6 }}{3}$.

Xét tam giác $A'HK$: $\dfrac{1}{{H{L^2}}} = \dfrac{1}{{H{K^2}}} + \dfrac{1}{{A'{H^2}}}$$\Rightarrow HL = \dfrac{{\sqrt {22} }}{{11}}$.

• Xác định giao điểm của $MN$ và $\left( {SAC} \right)$:

ü Chọn mp chứa $MN$ là mp$\left( {SBN} \right)$

ü Giao tuyến $\left( {SBN} \right) \cap \left( {SAC} \right) = SI$ (với $I = AC \cap BN$

Trong $\left( {SBN} \right)$ gọi $SI \cap MN = P$, suy ra $P = MN \cap \left( {SAC} \right)$.

• Xác định góc $\widehat {\left( {MN,\left( {SAC} \right)} \right)}$

- Ta có $A{C^2} = A{B^2} + B{C^2} = 2{a^2}$; $C{D^2} = C{K^2} + K{D^2} = 2{a^2}$; $A{D^2} = {\left( {2a} \right)^2} = 4{a^2}$ $\Rightarrow A{C^2} + C{D^2} = A{D^2}$ $\Rightarrow \Delta ACD$ vuông tại $C$ $\Rightarrow CD \bot AC$ mà $CD \bot SA$ nên $CD \bot \left( {SAC} \right)$

- Góc $\widehat {\left( {MN,\left( {SAC} \right)} \right)} = \widehat {\left( {MN,PC} \right)} = \widehat {NPC}$

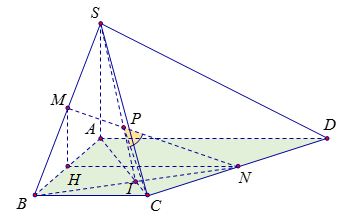
• Tính góc $\widehat {NPC}$:

ü Ta có $NC = \dfrac{{CD}}{2} = \dfrac{{a\sqrt 2 }}{2}$.

ü Ta có $I$ là trung điểm $BN$ và $M$ là trung điểm $SB$ suy ra $P$ là trọng tâm $\Delta SBN$ $\Rightarrow PN = \dfrac{2}{3}MN$

ü Gọi $H$ trung điểm $AB$ suy ra $MH{\rm{//}}SA$ do đó $\Delta MNH$ vuông tại $H$. $\Rightarrow MN = \sqrt {M{H^2} + H{N^2}}$ $= \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a + 2a}}{2}} \right)}^2}}  = \dfrac{{a\sqrt {10} }}{2}$ do đó $PN = \dfrac{2}{3}MN = \dfrac{{a\sqrt {10} }}{3}$.

Từ đó suy ra $PC = \sqrt {P{N^2} - N{C^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt {10} }}{3}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}}  = \dfrac{{a\sqrt {22} }}{6}$

• Cosin của góc $\widehat {NPC}$: $\cos \widehat {NPC} = \dfrac{{PC}}{{PN}} = \dfrac{{\dfrac{{a\sqrt {22} }}{6}}}{{\dfrac{{a\sqrt {10} }}{3}}} = \dfrac{{\sqrt {55} }}{{10}}$.

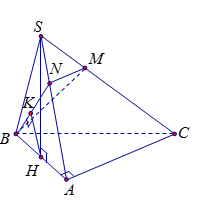
Cách 1. Gọi $H$ là trung điểm của $AB$ suy ra $SH \bot \left( {ABC} \right).$

Trong $\left( {SAC} \right)$ từ $M$ dựng $MN\;{\rm{//}}\;AC$, gọi $K$ là hình chiếu của $H$ trên $BN.$

Ta có $AC \bot \left( {SAB} \right)$ mà $MN\;{\rm{//}}\;AC \Rightarrow MN \bot \left( {SAB} \right)$

$\left\{ {\begin{array}{*{20}{c}}{HK \bot BN}\\{HK \bot MN}\end{array}} \right. \Rightarrow HK \bot \left( {BMN} \right).$

 Vì $\left( {BMN} \right)\;{\rm{//}}\;AC$ suy ra khoảng cách giữa hai đường $AC$ và $BM$ là

$d\left( {A,\left( {BMN} \right)} \right) = 2d\left( {H,\left( {BMN} \right)} \right) = 2HK = 2BH\sin \widehat {ABN}$

Trong tam giác $SAB$ hạ $NF \bot AB$, suy ra $NF = \dfrac{2}{3}SH = \dfrac{2}{3}.\dfrac{{4\sqrt 3 }}{2} = \dfrac{{4\sqrt 3 }}{3}$, và

$BF = BH + HF = BH + \dfrac{1}{3}AH = 2 + \dfrac{2}{3} = \dfrac{8}{3}$.  

Vậy $BN = \sqrt {B{F^2} + N{F^2}}  = \dfrac{{a\sqrt 7 }}{3}$, $\dfrac{{BN}}{{\sin 60^\circ }} = \dfrac{{AN}}{{\sin \widehat {ABN}}}$$\Leftrightarrow \sin \widehat {ABN} = \dfrac{{\dfrac{{2a}}{3}.\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 7 }}{3}}} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}.$

Suy ra $d\left( {A,\left( {BMN} \right)} \right) = 2.2.\dfrac{{\sqrt 3 }}{{\sqrt 7 }} = \dfrac{{4\sqrt {21} }}{7}.$

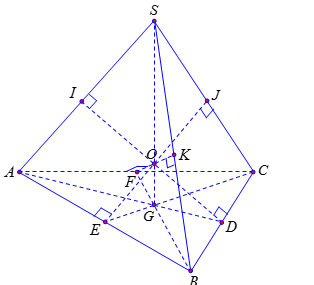
Ta có khối chóp $S.ABC$ là khối chóp tam giác đều.

Gọi $G$ là trọng tâm tam giác $ABC$. Khi đó $SG$ là chiều cao của khối chóp $S.ABC$.

Gọi $D$,$E$,$F$lần lượt là trung điểm của $BC$,$AB$,$CA$ và $I$,$J$,$K$ lần lượt là hình chiếu của $D$,$E$,$F$ trên $SA$,$SC$,$SB$.

Khi đó $DI$,$EJ$,$FK$tương ứng là các đường vuông góc chung của các cặp cạnh $SA$ và $BC$, $SC$ và $AB$, $SB$ và $CA$.

Ta có $DI = EJ = FK$. Do đó $\Delta SID = \Delta SJE$ nên $SI = SJ$.

Suy ra $ED//IJ$ (cùng song song với $AC$). Do đó bốn điểm $D$,$E$,$I$,$J$ đồng phẳng.

Tương tự ta có bộ bốn điểm $D$,$F$,$I$,$K$ và $E$,$F$,$J$,$K$ đồng phẳng.

Ba mặt phẳng $\left( {DEIJ} \right)$,$\left( {DFIK} \right)$,$\left( {EFJK} \right)$ đôi một cắt nhau theo ba giao tuyến $DI$, $EJ$, $FK$. Suy ra $DI$,$EJ$,$FK$ đồng quy tại điểm $O$ thuộc $SG$.

Xét điểm $M$bất kì trong không gian.

Ta có $\left\{ \begin{array}{l}d\left( {M,SA} \right) + d\left( {M,BC} \right) \ge DI\\d\left( {M,SC} \right) + d\left( {M,AB} \right) \ge EJ\\d\left( {M,SB} \right) + d\left( {M,AC} \right) \ge FK\end{array} \right. \Rightarrow d \ge DI + EJ + FK$.

Do đó $d$ nhỏ nhất bằng $DI + EJ + FK = 3DI$ khi $M \equiv O$.

Ta có $AD = \dfrac{{a\sqrt 3 }}{2}$, $AG = \dfrac{2}{3}AD = \dfrac{{a\sqrt 3 }}{3}$, $SG = \sqrt {S{A^2} - A{G^2}}  = \dfrac{{2a\sqrt 6 }}{3}$, $\sin \widehat {SAG} = \dfrac{{SG}}{{SA}} = \dfrac{{2\sqrt 2 }}{3}$.

Suy ra $DI = AD.\sin \widehat {SAD} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{2\sqrt 2 }}{3} = \dfrac{{a\sqrt 6 }}{3}$.

Vậy giá trị nhỏ nhất cần tìm là $3DI = 3\dfrac{{a\sqrt 6 }}{3} = a\sqrt 6$.

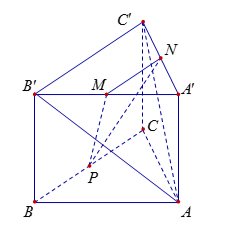
Gọi $I$, $Q$ lần lượt là trung điểm của $MN$, $B'C'$. Gọi $O = PI \cap AQ$.

Khi đó $\left\{ \begin{array}{l}O \in \;\left( {AB'C'} \right) \cap \left( {MNP} \right)\\B'C'\;{\rm{//}}\;MN\\B'C' \subset \left( {AB'C'} \right),\;MN \subset \left( {MNP} \right)\end{array} \right.$ nên giao tuyến của $\left( {AB'C'} \right)$ và $\left( {MNP} \right)$ là đường thẳng $d$ qua $O$ và song song $MN$, $B'C'$.

Tam giác $AB'C'$ cân tại $A$ nên $AQ \bot B'C' \Rightarrow AQ \bot d$.

Tam giác $PMN$ cân tại $P$ nên $PI \bot MN \Rightarrow PI \bot d$.

Do đó góc tạo bởi hai mặt phẳng $\left( {AB'C'} \right)$ và $\left( {MNP} \right)$ là góc giữa $AQ$ và $PI$.

Ta có $AP = 3$, $AQ = \sqrt {13}$, $IP = \dfrac{5}{2}$.

Vì  và $\dfrac{{AP}}{{IQ}} = 2$ nên $OA = \dfrac{2}{3}AQ = \dfrac{{2\sqrt {13} }}{3}$; $OP = \dfrac{2}{3}IP = \dfrac{5}{3}$.

$\cos \left( {\widehat {\left( {AB'C'} \right),\left( {MNP} \right)}} \right)$$= \cos \left( {\widehat {AQ,PI}} \right)$$= \left| {\cos \left( {\widehat {AOP}} \right)} \right|$$= \dfrac{{O{A^2} + O{P^2} - A{P^2}}}{{2OA.OP}}$$= \dfrac{{\sqrt {13} }}{{65}}$.

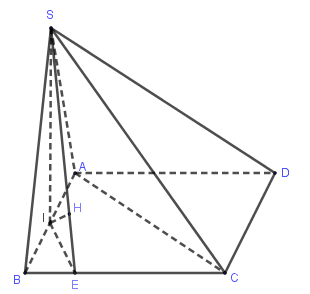
Gọi $I$ là trung điểm $AB$. Khi đó, ta có: $SI \bot \left( {ABCD} \right)$.

Do $AD{\rm{//}}BC$ nên$d\left( {AD,SC} \right) = d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right) = 2d\left( {I,\left( {SBC} \right)} \right)$

Xét $\Delta ABD$ có $DI$ là trung tuyến nên $DI = \sqrt {\dfrac{{D{A^2} + D{B^2}}}{2} - \dfrac{{A{B^2}}}{4}}  = \dfrac{{a\sqrt 7 }}{2}$.

Suy ra $SI = DI.\tan 60^\circ  = \dfrac{{a\sqrt {21} }}{2}$.

Từ $I$ kẻ $IE$ vuông góc với $BC$. Từ $I$ kẻ $IH$ vuông góc với $SE$. Khi đó, ta chứng minh được $IH = d\left( {I,\left( {SBC} \right)} \right)$.

Do $I$ là trung điểm $AB$ trong $\Delta ABC$ đều nên $IE = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}$.

Vậy $\dfrac{1}{{I{H^2}}} = \dfrac{1}{{I{S^2}}} + \dfrac{1}{{I{E^2}}} = \dfrac{{116}}{{21{a^2}}}$ hay $IH = \dfrac{{\sqrt {609} }}{{58}}$.

Kết luận: $d\left( {AD,SC} \right) = \dfrac{{\sqrt {609} }}{{29}}$.

Gọi $O = AC \cap BD$, $I = AM \cap SO$.

Trong $\left( {SBD} \right)$ từ $I$ kẻ đường thẳng $\Delta$ song song với $BD$ cắt  $SB$, $SD$ lần lượt tại $N$, $P$.

Suy ra thiết diện là tứ giác $ANMP$.

Ta có: $\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right.$$\Rightarrow BD \bot \left( {SAC} \right)$

$\Rightarrow BD \bot AM$.

Mặt khác: $BD//NP$.

$\Rightarrow AM \bot NP$.

$\Rightarrow {S_{ANMP}} = \dfrac{1}{2}NP.AM$.

+ Tính $AM$:

Ta có: $\left\{ \begin{array}{l}SA = SC = a\\AC = a\sqrt 2 \end{array} \right.$$\Rightarrow \Delta SAC$ vuông cân tại $S$.

$\Rightarrow AM = \sqrt {S{A^2} + S{M^2}}$$= \sqrt {{a^2} + {{\left( {\dfrac{2}{3}a} \right)}^2}}$$= \dfrac{{a\sqrt {13} }}{3}$.

+ Tính $AM$:

Ta có: $NP//BD$$\Rightarrow \dfrac{{NP}}{{BD}} = \dfrac{{SI}}{{SO}}$$\Rightarrow NP = \dfrac{{SI.BD}}{{SO}}$.

• Tính $\dfrac{{SI}}{{SO}}$:

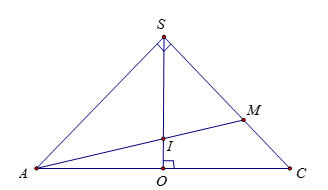
Gọi $\dfrac{{SI}}{{SO}} = k$.

Ta có: $\overrightarrow {AI}  = \overrightarrow {AS}  + \overrightarrow {SI}$$=  - \overrightarrow {SA}  + k\overrightarrow {SO}$.

          $\overrightarrow {AM}  = \overrightarrow {AS}  + \overrightarrow {SM}$$=  - \overrightarrow {SA}  + \dfrac{2}{3}\overrightarrow {SC}$.

$A$, $I$, $M$ thẳng hàng $\Leftrightarrow$ $\overrightarrow {AI}  = l\overrightarrow {AM}$$\Leftrightarrow  - \overrightarrow {SA}  + k\overrightarrow {SO}  =  - \overrightarrow {lSA}  + \dfrac{2}{3}l\overrightarrow {SC}$

$\Leftrightarrow  - \overrightarrow {SA}  + \dfrac{k}{2}\left( {\overrightarrow {SA}  + \overrightarrow {SC} } \right) =  - \overrightarrow {lSA}  + \dfrac{2}{3}l\overrightarrow {SC}$$\Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{2}k + l = 1\\\dfrac{1}{2}k - \dfrac{2}{3}l = 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{4}{5}\\l = \dfrac{3}{5}\end{array} \right.$ .

$\Rightarrow \dfrac{{SI}}{{SO}} = \dfrac{4}{5}$$\Rightarrow NP = \dfrac{4}{5}BD$$= \dfrac{{4a\sqrt 2 }}{5}$.

$\Rightarrow {S_{ANMP}} = \dfrac{1}{2}NP.AM$$= \dfrac{1}{2}.\dfrac{{4a\sqrt 2 }}{5}.\dfrac{{a\sqrt {13} }}{3}$$= \dfrac{{2\sqrt {26} {a^2}}}{{15}}$.

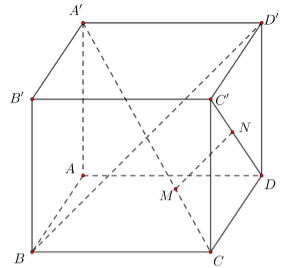
Đặt $\overrightarrow {AB}  = \vec a$, $\overrightarrow {AD}  = \vec b$, $\overrightarrow {AA'}  = \vec c$.

Từ $\overrightarrow {MA'}  = k.\overrightarrow {MC}$ $\Rightarrow \overrightarrow {AA'}  - \overrightarrow {AM}  = k\left( {\overrightarrow {AC}  - \overrightarrow {AM} } \right)$ $\Rightarrow \overrightarrow {AM}  = \dfrac{{\overrightarrow {AA'}  - k\overrightarrow {AC} }}{{1 - k}} = \dfrac{{ - k\left( {\vec a + \vec b} \right) + \vec c}}{{1 - k}}$.

và $\overrightarrow {NC'}  = l.\overrightarrow {ND}$ $\Rightarrow \overrightarrow {AC'}  - \overrightarrow {AN}  = l.\left( {\overrightarrow {AD}  - \overrightarrow {AN} } \right)$$\Leftrightarrow \overrightarrow {AN}  = \dfrac{{\overrightarrow {AC'}  - l\overrightarrow {AD} }}{{1 - l}} = \dfrac{{\vec a + \vec b + \vec c - l\vec b}}{{1 - l}}$.

Vậy $\overrightarrow {MN}  = \overrightarrow {AM}  - \overrightarrow {AN}$$= \dfrac{{ - k\left( {\vec a + \vec b} \right) + \vec c}}{{1 - k}} - \dfrac{{\vec a + \vec b + \vec c - l\vec b}}{{1 - l}}$

$= \left( { - \dfrac{k}{{1 - k}} - \dfrac{1}{{1 - l}}} \right)\vec a + \left( { - \dfrac{k}{{1 - k}} - 1} \right)\vec b + \left( {\dfrac{1}{{1 - k}} - \dfrac{1}{{1 - l}}} \right)\vec c$.

Mặt khác, $\overrightarrow {BD'}  = \overrightarrow {AD'}  - \overrightarrow {AB}  =  - \vec a + \vec b + \vec c$.

Để $MN{\rm{//}}BD'$ thì $\overrightarrow {MN} {\rm{//}}\overrightarrow {BD'}$ $\Rightarrow \left\{ \begin{array}{l}\dfrac{k}{{1 - k}} + \dfrac{1}{{1 - l}} =  - \dfrac{k}{{1 - k}} - 1\\ - \dfrac{k}{{1 - k}} - 1 = \dfrac{1}{{1 - k}} - \dfrac{1}{{1 - l}}\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2k}}{{1 - k}} + \dfrac{1}{{1 - l}} =  - 1\\\dfrac{{k + 1}}{{1 - k}} - \dfrac{1}{{1 - l}} =  - 1\end{array} \right.$

$\Rightarrow \dfrac{{3k + 1}}{{1 - k}} =  - 2$ $\Leftrightarrow k =  - 3$. Từ đó ta có: $\dfrac{1}{{1 - l}} = \dfrac{1}{2}$ $\Rightarrow l =  - 1$.

Vậy $k + l =  - 4$.

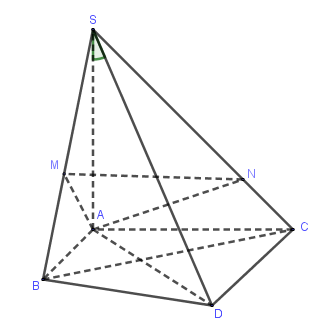
Kẻ đường kính $AD$ của đường tròn ngoại tiếp $\Delta ABC$ nên $\widehat {ABD} = \widehat {ACD} = 90^\circ$.

Ta có $\left\{ \begin{array}{l}BD \bot BA\\BD \bot SA\end{array} \right.$ $\Rightarrow BD \bot \left( {SAB} \right)$ hay $BD \bot AM$ và $AM \bot SB$ hay $AM \bot \left( {SBD} \right)$$\Rightarrow AM \bot SD$. Chứng minh tương tự ta được $AN \bot SD$. Suy ra $SD \bot \left( {AMN} \right)$, mà $SA \bot \left( {ABC} \right)$ $\Rightarrow \left( {\left( {ABC} \right),\left( {AMN} \right)} \right) = \left( {SA,SD} \right) = \widehat {DSA}$.

Ta có $BC = 2R\sin A$$= AD.\dfrac{{\sqrt 3 }}{2}$$\Rightarrow SA = 2BC = AD\sqrt 3$.

Vậy $\tan \widehat {ASD} = \dfrac{{AD}}{{SA}}$$= \dfrac{1}{{\sqrt 3 }}$$\Rightarrow \widehat {ASD} = 30^\circ$.

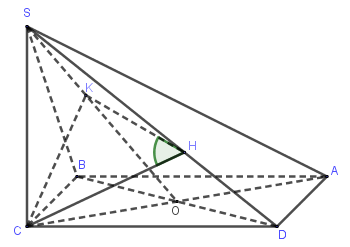
Từ $SC \bot \left( {ABCD} \right) \Rightarrow SC \bot BD$.

Từ $\left\{ \begin{array}{l}BD \bot SC\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)$.

Kẻ $CK \bot SO$, từ $BD \bot \left( {SAC} \right) \Rightarrow BD \bot CK$. Như vậy $CK \bot \left( {SBD} \right) \Rightarrow CK \bot SD$.

Kẻ $CH \bot SD$, do $CK \bot SD$ nên suy ra $SD \bot \left( {CHK} \right)$.

Mặt khác $\left( {CHK} \right) \cap \left( {SBD} \right) = HK$ và $\left( {CHK} \right) \cap \left( {SCD} \right) = CK$ nên góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$ bằng $\widehat {CHK}$.

Trong tam giác $SCD$ vuông tại $C$, ta có:

$\dfrac{1}{{C{H^2}}} = \dfrac{1}{{C{D^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{2}} \right)}^2}}} = \dfrac{5}{{3{a^2}}} \Rightarrow CH = \dfrac{{a\sqrt 3 }}{{\sqrt 5 }}$.

Vì $ABCD$ là hình thoi cạnh bằng $a$ và góc $A$ bằng $60^\circ$ nên $CO = \dfrac{{a\sqrt 3 }}{2}$.

Trong tam giác $SCO$ vuông tại $C$, ta có:

$\dfrac{1}{{C{K^2}}} = \dfrac{1}{{C{O^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{2}} \right)}^2}}} = \dfrac{2}{{{a^2}}} \Rightarrow CK = \dfrac{a}{{\sqrt 2 }}$.

Xét tam giác $CHK$ vuông tại $K$, ta có

$HK = \sqrt {C{H^2} - C{K^2}}  = \sqrt {\dfrac{{3{a^2}}}{5} - \dfrac{{{a^2}}}{2}}  = \dfrac{a}{{\sqrt {10} }}$.

$\cos \widehat {CHK} = \dfrac{{HK}}{{CH}} = \dfrac{a}{{\sqrt {10} }}:\dfrac{{a\sqrt 3 }}{{\sqrt 5 }} = \dfrac{{\sqrt 6 }}{6}$.

Vậy, cô-sin của góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$ bằng $\dfrac{{\sqrt 6 }}{6}$.

Dễ thấy $\widehat {SBA} = 45^\circ$.  Ta có $B'D' \bot SC$ và $BD \bot SC$ và $SC$ không vuông góc  với mặt phẳng $\left( {SBD} \right)$, suy ra $BD//B'D'$. Nên từ $I = SO \cap AC'$ nên từ $I$ kẻ $B'D'//BD$ cắt $SB$, $SD$ lần lượt tại $B'$ , $D'$.

Từ trên suy ra $B'D' \bot AC'$ và $\left\{ \begin{array}{l}AB' \bot SC\\AB' \bot BC\end{array} \right. \Rightarrow AB' \bot SB$.

 Suy ra ${S_{AB'C'D'}} = \dfrac{1}{2}AC'.B'D'$. Mà $AC' = \dfrac{{a\sqrt 6 }}{3}$ và $\dfrac{{B'D'}}{{BD}} = \dfrac{{SB'}}{{SB}} = \dfrac{{a\sqrt 2 }}{{2.a\sqrt 2 }} = \dfrac{1}{2}$$\Rightarrow B'D' = \dfrac{{a\sqrt 2 }}{2}$.

Vậy ${S_{AB'C'D'}} = \dfrac{1}{2}AC'.B'D' = \dfrac{{\sqrt 3 }}{6}{a^2}$.

Ta sử dụng phương pháp trải đa diện

Cắt hình chóp theo cạnh bên $SA$ rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau

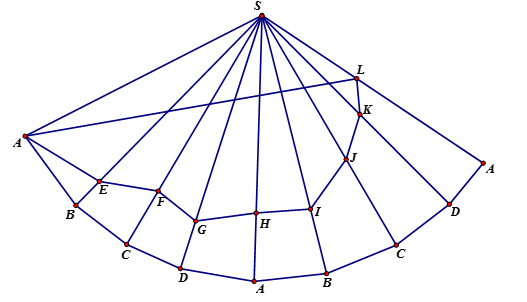
Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng $AL + LS$.

Từ giả thiết về hình chóp đều $S.ABCD$ta có $\widehat {ASL} = 120^\circ$.

Ta có $A{L^2} = S{A^2} + S{L^2} - 2SA.SL.\cos \widehat {ASL} = {200^2} + {40^2} - 2.200.40.\cos 120^\circ  = 49600$.

Nên $AL = \sqrt {49600}  = 40\sqrt {31}$.

Vậy, chiều dài dây đèn led cần ít nhất là $40\sqrt {31}  + 40$ mét.

Kéo dài MN cắt AB và AD lần lượt tại E và F.

Gọi $H = A'E \cap BB';\,\,K = A'F \cap DD'$. Khi đó thiết diện là A’HMNK.

Ta có ABMND là hình chiếu của A’HMNK trên mặt phẳng $\left( {ABCD} \right)$.

Gọi $I = AC \cap MN$ ta có: $AC \bot BD;\,\,MN//BD \Rightarrow AC \bot MN$ tại I.

$\left\{ \begin{array}{l}MN \bot AI\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {A'AI} \right) \Rightarrow MN \bot A'I$

$\Rightarrow \widehat {\left( {\left( {A'HMNK} \right);\left( {ABCD} \right)} \right)} = \widehat {AIA'}$

Ta có :

$CM = CN = 1 \Rightarrow MN = \sqrt 2  \Rightarrow IC = \dfrac{{\sqrt 2 }}{2}$

$AC = 2\sqrt 2  \Rightarrow AI = 2\sqrt 2  - \dfrac{{\sqrt 2 }}{2} = \dfrac{{3\sqrt 2 }}{2}$.

Xét tam giác vuông AA’I có: $A'I = \sqrt {AA{'^2} + A{I^2}}  = \sqrt {4 + \dfrac{9}{2}}  = \dfrac{{\sqrt {34} }}{2}$.

$\Rightarrow \cos \widehat {AIA'} = \dfrac{{AI}}{{A'I}} = \dfrac{{\dfrac{{3\sqrt 2 }}{2}}}{{\dfrac{{\sqrt {34} }}{2}}} = \dfrac{3}{{\sqrt {17} }} = \cos \widehat {\left( {\left( {ABCD} \right);\left( {A'HMNK} \right)} \right)}$

Ta có ${S_{ABCD}} = 4;\,\,{S_{CMN}}\dfrac{1}{2}.1.1 = \dfrac{1}{2} \Rightarrow {S_{ABMND}} = 4 - \dfrac{1}{2} = \dfrac{7}{2}$

$\Rightarrow {S_{A'HMNK}} = \dfrac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}} = \dfrac{7}{2}.\dfrac{{\sqrt {17} }}{3} = \dfrac{{7\sqrt {17} }}{6}$ .

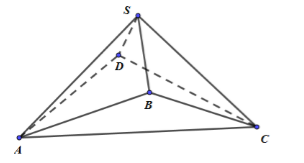
Chóp tứ giác S.ABCD có:  $SA' = SB' = SC' = SD = 1$ và  $\widehat {A'SB'} = \widehat {B'SC'} = \widehat {C'SD} = \widehat {DSA'} = {60^0}$

$\Rightarrow S.A'B'C'D$ là chóp tứ giác đều.

+) Tính khoảng cách từ A’ đến (SC’D):

$\left\{ \begin{array}{l}A'C' \cap (SC'D) = C'\\A'C' = 2.OC'\end{array} \right. \Rightarrow d(A';(SC'D)) = 2.d(O;(SC'D))$

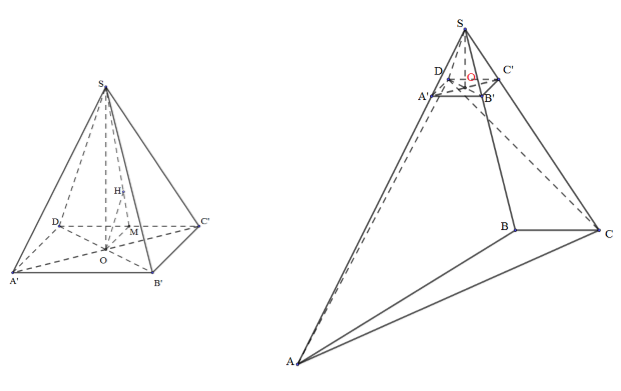
Ta có : $OM = \dfrac{{A'D}}{2} = \dfrac{1}{2}$, $OC = \dfrac{{\sqrt 2 }}{2}.1 = \dfrac{{\sqrt 2 }}{2}$

$\Delta SOC'$ vuông tại O  $\Rightarrow SO = \sqrt {SC{'^2} - OC{'^2}}  = \sqrt {1 - {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}  = \dfrac{{\sqrt 2 }}{2}$

$\Delta SOM$ vuông tại O, $OH \bot SM \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}} = \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{1}{2}} \right)}^2}}} = 6 \Rightarrow OH = \dfrac{1}{{\sqrt 6 }}$

$\Rightarrow d(O;(SC'D)) = \dfrac{1}{{\sqrt 6 }} \Rightarrow d(A';(SC'D)) = \dfrac{2}{{\sqrt 6 }}$

+) Vì $\left\{ \begin{array}{l}SA \cap (SC'D) = C'\\SA = 4.SA'\end{array} \right. \Rightarrow d(A;(SC'D)) = 4.d(A';(SC'D)) = 4.\dfrac{2}{{\sqrt 6 }} = \dfrac{8}{{\sqrt 6 }} = \dfrac{{4\sqrt 6 }}{3}$

Vậy,  khoảng cách từ A đến (SCD) là $\dfrac{{4\sqrt 6 }}{3}$.

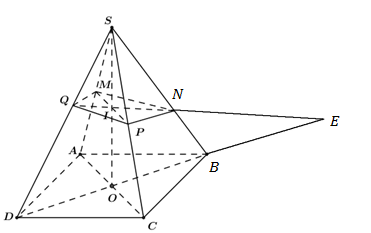
Gọi O là tâm hình bình hành ABCD.

Gọi I là giao điểm của SO và MP.

Trong mặt phẳng (SBD), kéo dài NI cắt SD tại Q, cắt BD tại E.

Áp dụng định lí Menelaus trong tam giác SOB ta có : $\dfrac{{MS}}{{MO}}.\dfrac{{EO}}{{EB}}.\dfrac{{NB}}{{NS}} = 1 \Leftrightarrow 1.\dfrac{{EO}}{{EB}}.\dfrac{1}{2} = 1 \Rightarrow \dfrac{{EO}}{{EB}} = 2$

$\Rightarrow \dfrac{{ED}}{{EB}} = 3$

Áp dụng định lí Menelaus trong tam giác SBD ta có : $\dfrac{{QS}}{{QD}}.\dfrac{{ED}}{{EB}}.\dfrac{{NB}}{{NS}} = 1 \Leftrightarrow \dfrac{{QS}}{{QD}}.3.\dfrac{1}{2} = 1 \Leftrightarrow \dfrac{{QS}}{{QD}} = \dfrac{2}{3}$

$\Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{2}{5}$