Câu hỏi:
2 năm trước
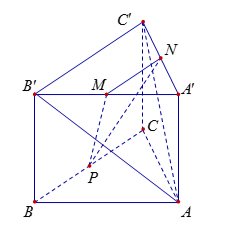
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = 2\sqrt 3 \) và $AA' = 2$. Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm các cạnh \(A'B'\), \(A'C'\) và \(BC\) (tham khảo hình vẽ bên dưới). Côsin của góc tạo bởi hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {MNP} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
Gọi \(I\), \(Q\) lần lượt là trung điểm của \(MN\), $B'C'$. Gọi \(O = PI \cap AQ\).
Khi đó \(\left\{ \begin{array}{l}O \in \;\left( {AB'C'} \right) \cap \left( {MNP} \right)\\B'C'\;{\rm{//}}\;MN\\B'C' \subset \left( {AB'C'} \right),\;MN \subset \left( {MNP} \right)\end{array} \right.\) nên giao tuyến của \(\left( {AB'C'} \right)\) và \(\left( {MNP} \right)\) là đường thẳng \(d\) qua \(O\) và song song \(MN\), \(B'C'\).
Tam giác \(AB'C'\) cân tại \(A\) nên \(AQ \bot B'C' \Rightarrow AQ \bot d\).
Tam giác \(PMN\) cân tại \(P\) nên \(PI \bot MN \Rightarrow PI \bot d\).
Do đó góc tạo bởi hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {MNP} \right)\) là góc giữa \(AQ\) và \(PI\).
Ta có \(AP = 3\), \(AQ = \sqrt {13} \), \(IP = \dfrac{5}{2}\).
Vì và \(\dfrac{{AP}}{{IQ}} = 2\) nên \(OA = \dfrac{2}{3}AQ = \dfrac{{2\sqrt {13} }}{3}\); \(OP = \dfrac{2}{3}IP = \dfrac{5}{3}\).
$\cos \left( {\widehat {\left( {AB'C'} \right),\left( {MNP} \right)}} \right)$$ = \cos \left( {\widehat {AQ,PI}} \right)$$ = \left| {\cos \left( {\widehat {AOP}} \right)} \right|$$ = \dfrac{{O{A^2} + O{P^2} - A{P^2}}}{{2OA.OP}}$$ = \dfrac{{\sqrt {13} }}{{65}}$.
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng, sử dụng lý thuyết: Góc giữa hai mặt phẳng (khác \({90^0}\)) là góc giữa hai đường thẳng cùng vuông góc với giao tuyến.
- Tính góc vừa xác định được ở trên bằng kiến thức hình học đã biết.
