Cho hình chóp S.ABCD có đáy là hình bình hành (hình vẽ minh họa).
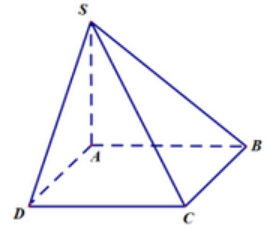
Hãy chọn khẳng định đúng.
Bước 1:
Gọi O là giao điểm của AC và BD.
Bước 2:
Khi đó O là trung điểm chung của AC và BD.
\(\begin{array}{l}\overrightarrow {SC} + \overrightarrow {SA} = 2\overrightarrow {SO} ;\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \\ \Rightarrow \overrightarrow {SC} + \overrightarrow {SA} = \overrightarrow {SB} + \overrightarrow {SD} \end{array}\)
Cho hình chóp \(O.\,ABC\) có ba cạnh \(OA,\,OB,\,OC\) đôi một vuông góc và \(OA = OB = OC = a\). Gọi \(M\) là trung điểm cạnh \(AB\). Góc hợp bởi hai véc tơ \(\overrightarrow {BC} \) và \(\overrightarrow {OM} \) bằng
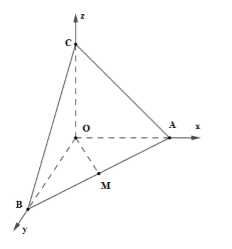
Gắn hệ trục tọa độ \(Oxyz\) như hình vẽ với \(A \in Ox;B \in Oy;C \in Oz\) và \(OA = OB = OC = a\)
Khi đó \(A\left( {a;0;0} \right),B\left( {0;a;0} \right),C\left( {0;0;a} \right) \Rightarrow M\left( {\dfrac{a}{2};\dfrac{a}{2};0} \right)\)
Ta có \(\overrightarrow {OM} = \left( {\dfrac{a}{2};\dfrac{a}{2};0} \right) \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{4} + 0} = \dfrac{{a\sqrt 2 }}{2}\) và \(\overrightarrow {BC} = \left( {0; - a;a} \right) \Rightarrow \left| {\overrightarrow {BC} } \right| = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Từ đó cos\(\left( {\overrightarrow {BC} ;\overrightarrow {OM} } \right) = \dfrac{{\overrightarrow {BC} .\overrightarrow {OM} }}{{\left| {\overrightarrow {BC} } \right|.\left| {\overrightarrow {OM} } \right|}} = \dfrac{{\dfrac{a}{2}.0 + \dfrac{a}{2}.\left( { - a} \right) + 0.a}}{{a\sqrt 2 .\dfrac{{a\sqrt 2 }}{2}}} = \dfrac{{ - \dfrac{{{a^2}}}{2}}}{{{a^2}}} = - \dfrac{1}{2}\)
Nên góc giữa hai véc tơ \(\overrightarrow {BC} ;\overrightarrow {OM} \) là \(120^\circ .\)
Trong không gian cho hai vectơ \(\vec u,\vec v\) tạo với nhau một góc \({120^0},|\vec u| = 4\) và \(|\vec v| = 3\). Tích vô hướng \(\vec u,\vec v\) bằng
\(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|\cos (\overrightarrow u ,\overrightarrow v ) = 4.3.\cos 120^\circ = - 6\)
Cho hình tứ diện ABCD, trọng tâm G. Mệnh đề nào sau đây đúng?
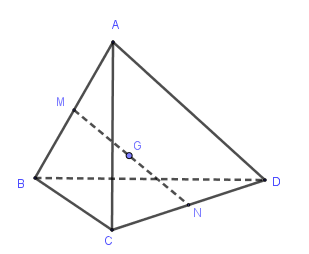
Gọi M, N lần lượt là trung điểm của AB, CD
$ \Rightarrow $ G là trung điểm của MN $ \Rightarrow \overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 $
$ \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $ $ \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = - \overrightarrow {GD} \ne \overrightarrow 0 $ $ \Rightarrow $B sai.
Ta có: $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OG} + \overrightarrow {GA} + \overrightarrow {OG} + \overrightarrow {GB} + \overrightarrow {OG} + \overrightarrow {GC} + \overrightarrow {OG} + \overrightarrow {GD} $
$ = 4\overrightarrow {OG} + (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} ) = 4\overrightarrow {OG} $ $ \Rightarrow \overrightarrow {OG} = \dfrac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)$$ \Rightarrow $A sai.
Khi O trùng A thì D đúng và C sai.
Cho ba vectơ $\vec a,\,\,\vec b,\,\,\vec c$ không đồng phẳng. Xét các vectơ $\vec x = 2\vec a + \vec b$, $\vec y = \vec a - \vec b - \vec c$, $\vec z = - \,3\vec b - \,2\vec c.$ Khẳng định nào dưới đây là đúng ?
Giả sử, ba vectơ $\vec x,\,\,\vec y,\,\,\vec z$ đồng phẳng, khi đó $\vec x = m.\vec y + n.\vec z$.
Ta có $\left\{ \begin{array}{l}m.\vec y = m.\vec a - m.\vec b - m.\vec c\\n.\vec z = - \,3n.\vec b - \,2n.\vec c\end{array} \right. $ $\Rightarrow m.\vec y + n.\vec z = m.\vec a - \left( {m + 3n} \right).\vec b - \left( {m + 2n} \right).\vec c.$
Khi đó $2\vec a + \vec b = m.\vec a - \left( {m + 3n} \right).\vec b - \left( {m + 2n} \right).\vec c \Rightarrow \left\{ \begin{array}{l}m = 2\\m + 3n = - \,1\\m + 2n = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2\\n = - \,1\end{array} \right..$
Vậy ba vectơ $\vec x,\,\,\vec y,\,\,\vec z$ đồng phẳng.
Cho $ABCD.{A_1}{B_1}{C_1}{D_1}$ là hình hộp, trong các khẳng định sau khẳng định sai:
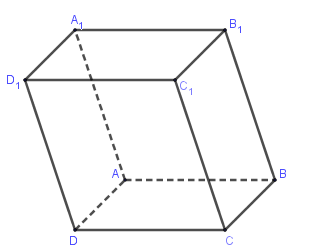
Xét đáp án A: \(\overrightarrow {A{C_1}} + \overrightarrow {{A_1}C} \)\( = \overrightarrow {AC} + \overrightarrow {C{C_1}} + \overrightarrow {{A_1}A} + \overrightarrow {AC} \) \( = 2\overrightarrow {AC} + \left( {\overrightarrow {C{C_1}} + \overrightarrow {{A_1}A} } \right) = 2\overrightarrow {AC} \) nên A đúng.
Xét đáp án B: \(\overrightarrow {A{C_1}} + \overrightarrow {C{A_1}} + 2\overrightarrow {{C_1}C} \) \( = \overrightarrow {A{C_1}} + \overrightarrow {C{A_1}} + \overrightarrow {{C_1}C} + \overrightarrow {{C_1}C} \) \( = \left( {\overrightarrow {A{C_1}} + \overrightarrow {{C_1}C} } \right) + \left( {\overrightarrow {C{A_1}} + \overrightarrow {{C_1}C} } \right)\) \( = \overrightarrow {AC} + \overrightarrow {{C_1}{A_1}} = \overrightarrow 0 \) nên B đúng.
Xét đáp án C: Do \(\overrightarrow {A{C_1}} + \overrightarrow {{A_1}C} = 2\overrightarrow {AC} \) và \(\overrightarrow {AC} \ne \overrightarrow {A{A_1}} \) nên C sai.
Xét đáp án D: \(\overrightarrow {C{A_1}} + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {C{A_1}} = \overrightarrow {A{A_1}} = \overrightarrow {C{C_1}} \) nên D đúng.
Cho $ABCD.{A_1}{B_1}{C_1}{D_1}$là hình hộp, với K là trung điểm CC1. Tìm khẳng định đúng trong các khẳng định sau:
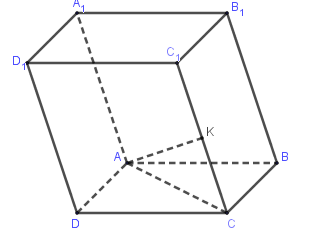
Có $\overrightarrow {AK} = \overrightarrow {AC} + \overrightarrow {CK} = (\overrightarrow {AB} + \overrightarrow {AD} ) + \dfrac{1}{2}\overrightarrow {A{A_1}} = \overrightarrow {AB} + \overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {A{A_1}} $
Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$, Tìm giá trị của k thích hợp để $\overrightarrow {AB} \,\, + \overrightarrow {{B_1}{C_1}} + \overrightarrow {D{D_1}} = k\overrightarrow {A{C_1}} $
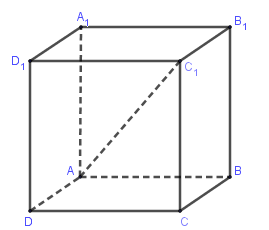
Có $\overrightarrow {AB} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {{\rm{D}}{{\rm{D}}_1}} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {C{C_1}} = \overrightarrow {A{C_1}} \Rightarrow k = 1$
Cho hình hộp $ABCD.{A_1}{B_1}{C_1}{D_1}$ với $M = C{D_1} \cap {C_1}D$. Khi đó:
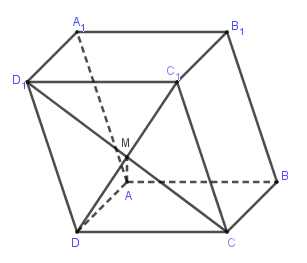
Ta có: $\overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {DM} = \overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {D{C_1}} $ $ = AD + \dfrac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {D{D_1}} } \right)$ $ = \overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {A{A_1}} $
Cho hình hộp \(ABCD.A'B'C'D'\). Đẳng thức nào sau đây là đẳng thức đúng?
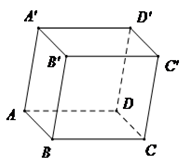
\(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BC'} \).
\(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD} '\)
Cho ba vectơ $\vec a,\,\,\vec b,\,\,\vec c$. Điều kiện nào dưới đây khẳng định ba vectơ $\vec a,\,\,\vec b,\,\,\vec c$ đồng phẳng ?
Dựa vào đáp án, ta thấy rằng:
+) Với $m + n + p = 0 \Rightarrow m = n = p = 0$ suy ra $m\vec a + n\vec b + p\vec c = \vec 0$ nên chưa kết luận được ba vectơ $\vec a,\,\,\vec b,\,\,\vec c$ đồng phẳng.
+) Với $m + n + p \ne 0$ suy ra tồn tại ít nhất một số khác $0.$
Giả sử $m \ne 0,$ ta có $m\vec a + n\vec b + p\vec c = \vec 0 \Leftrightarrow \vec a = - \dfrac{n}{m}.\vec b - \dfrac{p}{m}.\vec c.$
Suy ra tồn tại $n,\,\,p$ để ba vectơ $\vec a,\,\,\vec b,\,\,\vec c$ đồng phẳng.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, $AB = 6;AD = 4;$ $\overrightarrow {AB} .\overrightarrow {AD} = -12$ . Tính ${\left( {\overrightarrow {SC} - \overrightarrow {SA} } \right)^2}$
${\left( {\overrightarrow {SC} - \overrightarrow {SA} } \right)^2} = {\overrightarrow {AC} ^2} = {\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)^2} = {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2} + 2\overrightarrow {AB} .\overrightarrow {AD} $
$ = {6^2} + {4^2} + 2( - 12) = 28$
Cho tứ diện \(ABCD \) và điểm \(G\) thỏa $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $. Gọi \(O\) là giao điểm của \(GA\) và mặt phẳng \((BCD)\). Trong các khẳng định sau, khẳng định nào đúng?
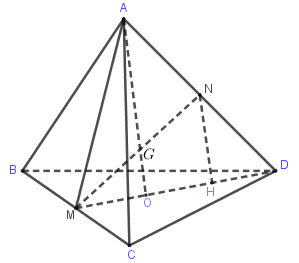
Gọi \(M, N\) là trung điểm của \(BC, AD\)
$ \Rightarrow $ \(G\) là trung điểm \(MN\). Gọi \(H \) là hình chiếu của \(N\) lên \(MD\)
$ \Rightarrow $ NH là đường trung bình của $\Delta AOD$ và \(OG \) là đường trung bình của $\Delta MNH$
$ \Rightarrow OG = \dfrac{1}{2}NH = \dfrac{1}{2}.\dfrac{1}{2}AO$ $ \Rightarrow OG = \dfrac{1}{2}NH = \dfrac{1}{4}.AO$ $ \Rightarrow \overrightarrow {GA} = 3\overrightarrow {OG} $
Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$ .Gọi \(M\) là trung điểm của \(AD\). Chọn khẳng định đúng:
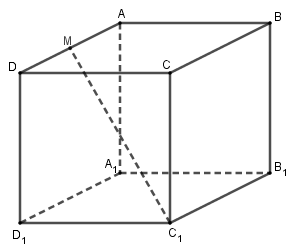
Đáp án A: \(\overrightarrow {{B_1}B} + \overrightarrow {{B_1}A{}_1} + \overrightarrow {{B_1}{C_1}} = \overrightarrow {{B_1}D} \ne \overrightarrow {{B_1}M} \) nên A sai.
Đáp án B: Ta có \(\overrightarrow {{C_1}M} = \overrightarrow {{C_1}{D_1}} + \overrightarrow {{{\rm{D}}_1}{\rm{D}}} + \overrightarrow {DM} = \overrightarrow {{C_1}{D_1}} + \overrightarrow {{C_1}C} + \dfrac{1}{2}\overrightarrow {{C_1}{B_1}} \) nên B đúng và C sai.
Đáp án D: \(\overrightarrow {B{B_1}} + \overrightarrow {{B_1}{A_1}} + \overrightarrow {{B_1}C{}_1} \) \( = \overrightarrow {B{A_1}} + \overrightarrow {{A_1}{D_1}} = \overrightarrow {B{D_1}} \ne 2\overrightarrow {{B_1}D} \) nên D sai.
Cho tứ diện \(ABCD\). Gọi M, N lần lượt là trung điểm của \(AD,BC\). Trong các khẳng định sau, khẳng định nào sai?
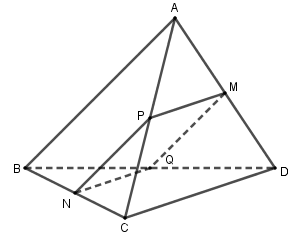
Gọi P, Q lần lượt là trung điểm AC, BD
$ \Rightarrow $ Ba vec tơ $\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN} $ có giá song song hoặc nằm trên mặt phẳng (MNPQ) nên 3 véc tơ này đồng phẳng $ \Rightarrow $ A đúng
Ba vec tơ $\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {MN} $ không đồng phẳng $ \Rightarrow $ B đúng
Ba vec tơ $\overrightarrow {AN} ,\overrightarrow {CM} ,\overrightarrow {MN} $ có giá không thể song song với mặt phẳng nào $ \Rightarrow $ C sai
Cho tứ diện \(ABCD\). Trên các cạnh \(AD,BC\) lần lượt lấy \(M, N\) sao cho $AM = 3MD;{\rm{ }}BN = 3NC$. Gọi \(P,Q\) lần lượt là trung điểm của $AD,BC$. Trong các khẳng định sau, khẳng định nào sai?
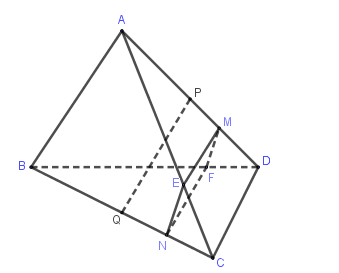
Lấy điểm E trên cạnh AC sao cho AE=3EC, lấy F trên BD sao cho BF=3FD
$\left\{ \begin{array}{l}NE//AB,NE = \dfrac{1}{3}AB\\MF//AB,MF = \dfrac{1}{3}AB\end{array} \right. \Rightarrow NE//MF,NE//MF$
$ \Rightarrow $ NEMF là hình bình hành và 3 vec tơ $\overrightarrow {BA} ,\,\overrightarrow {DC} ,\,\overrightarrow {MN} $ có giá song song hoặc nằm trên mặt phẳng (MFNE) $ \Rightarrow $$\overrightarrow {BA} ,\,\overrightarrow {DC} ,\,\overrightarrow {MN} $ đồng phẳng.
A đúng.
Gọi \(I,K\) lần lượt là trung điểm của \(AC,BD\).
Khi đó \(MN//\left( {PIQK} \right),\) \(DC//\left( {PIQK} \right),\) \(PQ \subset \left( {PIQK} \right)\) nên các véc tơ \(\overrightarrow {MN} ,\overrightarrow {DC} ,\overrightarrow {PQ} \) đồng phẳng.
B đúng.
Ta có: \(AB//\left( {PIQK} \right),\) \(DC//\left( {PIQK} \right),\) \(PQ \subset \left( {PIQK} \right)\) nên các véc tơ \(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {PQ} \) đồng phẳng.
C đúng.
Lại có: \(AC,DC \subset \left( {ADC} \right)\) nhưng \(MN \cap \left( {ACD} \right) = M\) nên ba véc tơ \(\overrightarrow {AC} ,\overrightarrow {DC} ,\overrightarrow {MN} \) không có giá song hoặc nằm trên mặt phẳng nào.
Vậy ba véc tơ này không đồng phẳng hay D sai.
Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$ . Khi đó tổng 3 góc $(\overrightarrow {{D_1}{A_1}} ,\overrightarrow {C{C_1}} ) + (\overrightarrow {{C_1}B} ,\overrightarrow {D{D_1}} ) + (\overrightarrow {D{C_1}} ,\overrightarrow {{A_1}B} )$ là:
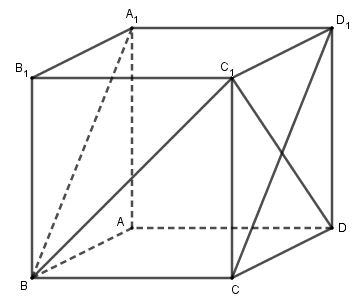
Ta có:
$\begin{array}{l}(\overrightarrow {{D_1}{A_1}} ,\overrightarrow {C{C_1}} ) = {90^0}\\(\overrightarrow {{C_1}B} ,\overrightarrow {D{D_1}} ) = (\overrightarrow {{C_1}B} ,\overrightarrow {C{C_1}} ) = {135^0}\\(\overrightarrow {D{C_1}} ,\overrightarrow {{A_1}B} ) = (\overrightarrow {D{C_1}} ,\overrightarrow {{D_1}C} ) = {90^0}\end{array}$
$ \Rightarrow (\overrightarrow {{D_1}{A_1}} ,\overrightarrow {C{C_1}} ) + (\overrightarrow {{C_1}B} ,\overrightarrow {D{D_1}} ) + (\overrightarrow {D{C_1}} ,\overrightarrow {{A_1}B} ) $ $= {90^0} + {135^0} + {90^0} = {315^0}$
Cho hình hộp ABCD.A’B’C’D’ (hình vẽ minh họa).
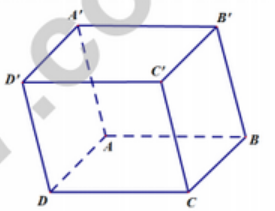
Mệnh đề nào sau đây đúng?
ACC’A’ và ABCD là hình bình hành nên: \(\overrightarrow {A{C^\prime }} = \overrightarrow {AC} + \overrightarrow {A{A^\prime }} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} \)
Chỉ ra mệnh đề đúng trong các mệnh đề sau:
Phương án A: sai vì chỉ cần giá của chúng song song hoặc nằm trên một mặt phẳng nào đó
Phương án B: sai vì ba véc tơ cùng phương \( \Leftrightarrow \overrightarrow a = k.\overrightarrow b = l.\overrightarrow c \)
Phương án C sai vì điều kiện cần và đủ để ba véc tơ đồng \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng là có các số \(m,n\) sao cho \(\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b \) (với \(\overrightarrow a ,\overrightarrow b \) không cùng phương).
Vậy chọn D
Cho hình tứ diện ABCD, trọng tâm G. Mệnh đề nào sau đây sai?
Gọi M, N lần lượt là trung điểm của AB, CD
$ \Rightarrow $ G là trung điểm của MN $ \Rightarrow \overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 $
$ \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $ nên B đúng
Ta có: $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OG} + \overrightarrow {GA} + \overrightarrow {OG} + \overrightarrow {GB} + \overrightarrow {OG} + \overrightarrow {GC} + \overrightarrow {OG} + \overrightarrow {GD} $
$ = 4\overrightarrow {OG} + (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} ) = 4\overrightarrow {OG} $ nên A đúng
Khi O trùng A thì D đúng vậy đáp án sai là C

