Cho ba vectơ →a,→b,→c không đồng phẳng xét các vectơ →x=2→a−→b;→y=−4→a+2→b; →z=−3→a−2→c
Chọn mệnh đề đúng trong các mệnh đề sau:
Ta thấy →y=−2→x nên →x,→y cùng phương.
Do đó ba véc tơ →x,→y,→z đồng phẳng.
D sai.
Cho hình lập phương ABCD.A1B1C1D1, Tìm giá trị của k thích hợp để →AB+→B1C1+→DD1=k→AC1
Có →AB+→B1C1+→DD1 =→AB+→BC+→CC1=→AC1 ⇒k=1
Cho hai điểm phân biệt A,B và một điểm O bất kì không thuộc đường thẳng AB. Mệnh đề nào sau đây là đúng?
Điểm M thuộc đường thẳng AB nếu và chỉ nếu →OM=k.→OA+(1−k).→OB.
Chứng minh:
Ta có: M∈AB⇔→MB=k→AB
Xen điểm O ta được: →OB−→OM=k(→OB−→OA) ⇔→OM=→OB−k(→OB−→OA) ⇔→OM=k→OA+(1−k)→OB.
Vậy C đúng.
Cho hình hộp ABCD.A′B′C′D′. Tìm giá trị của k thích hợp điền vào đẳng thức véc tơ: →AC+→BA′+k(→DB+→C′D)=→0.
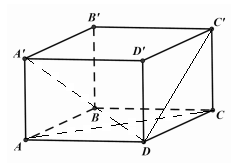
Với k=1 ta có: →AC+→BA′+1.(→DB+→C′D) =→AC+→BA′+→C′B =→AC+→C′A′=→AC+→CA=→0
Cho hình lăng trụ tam giác ABC.A1B1C1. Đặt →AA1=→a;→AB=→b;→AC=→c;→BC=→d trong các đẳng thức sau đẳng thức nào đúng.
Ta có: →b−→c+→d=→AB−→AC+→BC=→CB+→BC=→0
Trong các khẳng định sau đây, khẳng định nào sai?
Ba véc tơ đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng nên đáp án A sai.
Cho tứ diện ABCD có các cạnh đều bằng a. Hãy chỉ ra mệnh đề đúng trong các mệnh đề sau
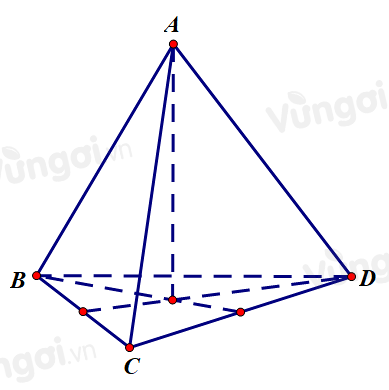
Phương án A:
→AD+→CD+→BC+→DA=(→AD+→DA)+(→BC+→CD)=→0+→BD≠→0 nên A sai
Phương án B:→AB.→AC=a.a.cos600=a22 nên B sai
Phương án C: →AC.→AD=→AC.→CD⇔→AC(→AD+→DC)=0⇔→AC2=0 nên C sai.
Phương án D: Do tứ diện ABCD đều nên AB⊥CD hay →AB.→CD=0.
Cho tứ diện đều ABCD,M là trung điểm của cạnh AB và G là trọng tâm cảu tam giác BCD. Đặt →AB=→b,→AC=→c,→AD=→d. Phân tích véc tơ →MG theo →d,→b,→c .
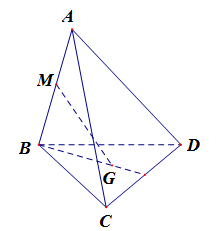
→MG=13(→MB+→MC+→MD)=13.12→AB+13(→MA+→AC)+13(→MA+→AD)=16→AB+23→MA+13→AC+13→AD=16→AB+23.(−12→AB)+13→AC+13→AD=−16→AB+13→AC+13→AD=−16→b+13→c+13→d
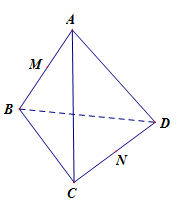
Cho tứ diện đều ABCD,M và N theo thứ tự là trung điểm của cạnh AB và CD. Mệnh đề nào sau đây sai?
A.Đúng vì: →AC+→BD=(→AD+→DC)+(→BC+→CD)=→AD+→BC
B. Đúng vì: →AD+→BC=(→AM+→MN+→ND)+(→BM+→MN+→NC) = 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {ND} + \overrightarrow {NC} } \right) = 2\overrightarrow {MN}
C.Đúng vì: \overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {AN} + 2\overrightarrow {BN} = 2\left( {\overrightarrow {AN} + \overrightarrow {BN} } \right) = - 2\left( {\overrightarrow {NA} + \overrightarrow {NB} } \right) = - 4\overrightarrow {NM}
Vậy D sai.
Cho tứ diện đều ABCD có tam giác BCD đều,AD = AC. Giá tri của \cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)là:
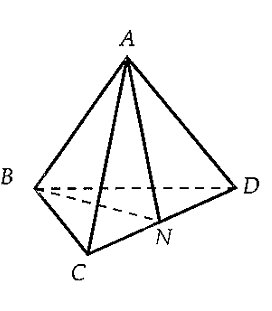
Gọi N là trung điểm của CD. Tam giác đều BCD nên BN \bot CD. Tam giác ACDcân tại A nên AN \bot CD ta có:
\overrightarrow {AB} .\overrightarrow {CD} = \left( {\overrightarrow {AN} + \overrightarrow {NB} } \right).\overrightarrow {CD} = \overrightarrow {AN} .\overrightarrow {CD} + \overrightarrow {NB} .\overrightarrow {CD} = 0 \Rightarrow c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = 0
Trong mặt phẳng \left( \alpha \right) cho tứ giác ABCD và một điểm S tùy ý. Mệnh đề nào sau đây đúng?
A. Sai vì \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {CD} \Leftrightarrow \overrightarrow {AC} - \overrightarrow {AB} + \overrightarrow {DC} - \overrightarrow {DB} = \overrightarrow 0 \Leftrightarrow B \equiv C (Vô lí)
B. Sai vì: Gọi O và O' theo thứ tự là trung điểm của AC và BD. Ta có
\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} và \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO'} \Leftrightarrow \overrightarrow {SO} = \overrightarrow {SO'} \Leftrightarrow O \equiv O' điều này không đúng nếu ABCD không phải là hình bình hành.
C. Đúng – Chứng minh tương tự như ý B.
D. sai vì: Gọi M,N lần lượt là trung điểm của AB,CD. Khi đó:
\begin{array}{l} \overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \\ \overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {ON} \\ \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \\ \Leftrightarrow 2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {OM} + \overrightarrow {ON} = \overrightarrow 0 \end{array}
Hay O là trung điểm MN. Điều này chưa chắc đúng nên D sai.
Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của AA', O là tâm của hình bình hành ABCD. Cặp ba vecto nào sau đây đồng phẳng?
Ta có MO{\rm{//}}\left( {CDA'B'} \right);
AB//A'B' \Rightarrow AB{\rm{//}}\left( {CDA'B'} \right),
B'C nằm trong mặt phẳng \left( {CDA'B'} \right) nên các vecto \overrightarrow {MO} ,\overrightarrow {AB} ,\overrightarrow {B'C} dồng phẳng vì có giá song song hay nằm trên mặt phẳng \left( {CDA'B'} \right).
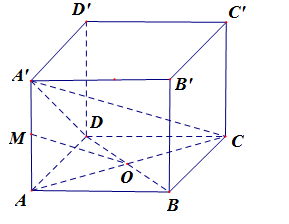
Cho tứ diện ABCD, M và N theo thứ tự là trung điểm của AB và CD. Bộ ba vecto nào dưới đây đồng phẳng?
\begin{array}{l}\overrightarrow {AD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \\\overrightarrow {BC} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} \\ \Rightarrow \overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {MN} \Rightarrow \overrightarrow {MN} = \dfrac{1}{2}\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {BC} \end{array}
Vậy ba vecto \overrightarrow {BC} ;\overrightarrow {AD} ;\overrightarrow {MN} đồng phẳng.
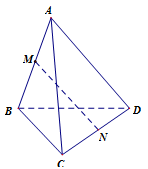
Cho tứ diện ABCD. M là điểm trên đoạn AB và MB = 2MA. N là điểm trên đường thẳng CD mà \overrightarrow {CN} = k\overrightarrow {CD} . Nếu \overrightarrow {MN} ,\overrightarrow {AD} ,\overrightarrow {BC} đồng phẳng thì giá trị của k là:
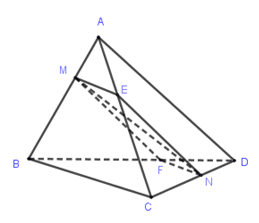
Qua M vẽ mặt phẳng \left( \alpha \right) song song với AD và BC.
\left( \alpha \right)cắt AC tại E, BD tại F và CD tại N. Ta có MF{\rm{//}}EN{\rm{//}}AD.
Các vecto \overrightarrow {MN} ,\overrightarrow {AD} ,\overrightarrow {BC} có giá song song hay nằm trong mặt phẳng \left( \alpha \right) nên đồng phẳng.
Ta có: \dfrac{{CN}}{{CD}} = \dfrac{{BF}}{{BD}} = \dfrac{{BM}}{{BA}} = \dfrac{2}{3}(Ta – let) nên \overrightarrow {CN} = \dfrac{2}{3}\overrightarrow {CD} .
Vậy k = \dfrac{2}{3}.
Cho hình lập phương ABCD.A'B'C'D', đặt \alpha = (\overrightarrow {AC} ,\overrightarrow {DC'} ); \beta = (\overrightarrow {DA'} ,\overrightarrow {B'B} ); \gamma = (\overrightarrow {AA'} ,\overrightarrow {C'C} ). Khi đố biểu thức \alpha + \beta + \gamma có giá trị là:
\alpha = (\overrightarrow {AC} ,\overrightarrow {DC'} ) = (\overrightarrow {AC} ,\overrightarrow {AB'} ) = {60^0}
(Vì tam giác AB'C đều cạnh AB'=B'C=AC đều là các đường chéo của các hình vuông cạnh bằng nhau)
\beta = (\overrightarrow {DA'} ,\overrightarrow {B'B} ) = (\overrightarrow {DA'} ,\overrightarrow {A'A} ) = 180^0-45^0={135^0}
\gamma = (\overrightarrow {AA'} ,\overrightarrow {C'C} ) = (\overrightarrow {AA'} ,\overrightarrow {A'A} ) = {180^0}
\Rightarrow \alpha + \beta + \gamma = {60^0} + {135^0} + {180^0} = {375^0}
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Hãy tìm mệnh đề sai trong các mệnh đề sau:
Xét phương án A có: \overrightarrow {AD'} .\overrightarrow {CC'} = \overrightarrow {AD'} .\overrightarrow {AA'} = \left| {\overrightarrow {AD'} } \right|.\left| {\overrightarrow {AA'} } \right|{\rm{cos4}}{{\rm{5}}^0} = {a^2}
Trong không gian cho hai tia Ax,By chéo nhau sao cho AB vuông góc với cả hai tia đó. Các điểm M,N lần lượt thay đổi trên Ax,By sao cho độ dài đoạn MN luôn bằng giá trị c không đổi (c~\le AB). Gọi \varphi là góc giữa Ax,By. Giá trị lớn nhất của AM.BN là:
Ta có:
\begin{array}{l}{c^2} = M{N^2} = {\overrightarrow {MN} ^2} = {\left( {\overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} } \right)^2} \\ = {\overrightarrow {MA} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {BN} ^2} + 2\overrightarrow {MA} .\overrightarrow {AB} + 2\overrightarrow {AB} .\overrightarrow {BN} + 2\overrightarrow {MA} .\overrightarrow {BN} \\ = A{M^2} + A{B^2} + B{N^2} + 2.0 + 2.0 + 2\overrightarrow {MA} .\overrightarrow {BN} \\= A{M^2} + A{B^2} + B{N^2} - 2\overrightarrow {AM} .\overrightarrow {BN} \\ = A{B^2} + A{M^2} + B{N^2} - 2AM.BN.\cos \varphi \end{array}
\ge A{B^2} + 2AM.BN - 2AM.BN\cos \varphi
= A{B^2} + 2AM.BN.(1 - \cos \varphi {\rm{)}}
\Rightarrow AM.BN \le \dfrac{{{c^2} - A{B^2}}}{{2(1 - \cos \varphi )}}
Vậy biểu thức AM.BN đạt giá trị lớn nhất bằng \dfrac{{{c^2} - A{B^2}}}{{2(1 - \cos \varphi )}}
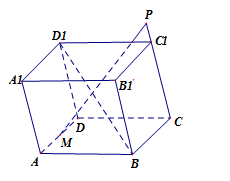
Cho hình hộp ABCD.{A_1}{B_1}{C_1}{D_1}. M là điểm trên cạnh AD sao cho \overrightarrow {AM} = \dfrac{1}{3}\overrightarrow {AD} . N là điểm trên đường thẳng B{D_1}. P là điểm trên đường thẳng C{C_1} sao cho M,N,P thẳng hàng.
Tính \dfrac{{\left| {\overrightarrow {MN} } \right|}}{{\left| {\overrightarrow {NP} } \right|}}.
Đặt \overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b ,\overrightarrow {A{A_1}} = \overrightarrow c và \overrightarrow {BN} = x\overrightarrow {B{D_1}} ;\overrightarrow {CP} = y\overrightarrow {C{C_1}} = y\overrightarrow c .
Ba điểm M,N,P thẳng hàng nên \overrightarrow {MN} = \alpha .\overrightarrow {NP} \left( 1 \right).
Ta có: \overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN}
\begin{array}{l} = - \dfrac{1}{3}\overrightarrow b + \overrightarrow a + x\overrightarrow {B{D_1}} \\ = - \dfrac{1}{3}\overrightarrow b + \overrightarrow a + x\left( {\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {B{B_1}} } \right)\\ = - \dfrac{1}{3}\overrightarrow b + \overrightarrow a + x\left( { - \overrightarrow a + \overrightarrow b + \overrightarrow c } \right) \\= \left( {1 - x} \right)\overrightarrow a + \left( {x - \dfrac{1}{3}} \right)\overrightarrow b + x\overrightarrow c {\rm{ }}\left( 2 \right)\end{array}
Ta lại có:
\begin{array}{l}\overrightarrow {NP} = \overrightarrow {NB} + \overrightarrow {BC} + \overrightarrow {CP} \\= - x\overrightarrow {B{D_1}} + \overrightarrow b + y\overrightarrow c \\= - x\left( {\overrightarrow b - \overrightarrow a + \overrightarrow c } \right) + \overrightarrow b + y\overrightarrow c \\ \Rightarrow \overrightarrow {NP} = x\overrightarrow a + \left( {1 - x} \right)\overrightarrow b + \left( {y - x} \right)\overrightarrow c {\rm{ }}\left( 3 \right)\end{array}
Thay (2), (3) vào (1) ta được:
\left\{ \begin{array}{l}1 - x = \alpha x\\x - \dfrac{1}{3} = \alpha \left( {1 - x} \right)\\x = \alpha \left( {y - x} \right)\end{array} \right. . Giải hệ ta được \alpha = \dfrac{2}{3},x = \dfrac{3}{5},y = \dfrac{3}{2}.
Vậy \dfrac{{\left| {\overrightarrow {MN} } \right|}}{{\left| {\overrightarrow {NP} } \right|}} = \dfrac{2}{3}.
Trong không gian, cho hình hộp ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }. Vectơ \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} bằng

ABCD là hình bình hành nên \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}
ACC'A' là hình bình hành \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'}
Trong không gian, với \vec a,\vec b là hai vectơ bất kỳ, mệnh đề nào dưới đây đúng ?
\vec a\vec b = |\vec a||\vec b|\cos (\vec a,\vec b)

