Câu hỏi:
2 năm trước
Cho hình lập phương $ABCD.A'B'C'D'$, đặt $\alpha = (\overrightarrow {AC} ,\overrightarrow {DC'} );$ $\beta = (\overrightarrow {DA'} ,\overrightarrow {B'B} );$ $\gamma = (\overrightarrow {AA'} ,\overrightarrow {C'C} )$. Khi đố biểu thức $\alpha + \beta + \gamma $ có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: b
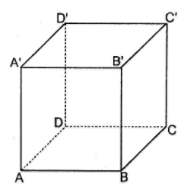
$\alpha = (\overrightarrow {AC} ,\overrightarrow {DC'} ) = (\overrightarrow {AC} ,\overrightarrow {AB'} ) = {60^0}$
(Vì tam giác \(AB'C\) đều cạnh $AB'=B'C=AC $ đều là các đường chéo của các hình vuông cạnh bằng nhau)
$\beta = (\overrightarrow {DA'} ,\overrightarrow {B'B} ) = (\overrightarrow {DA'} ,\overrightarrow {A'A} ) $ $= 180^0-45^0={135^0}$
$\gamma = (\overrightarrow {AA'} ,\overrightarrow {C'C} ) = (\overrightarrow {AA'} ,\overrightarrow {A'A} ) = {180^0}$
$ \Rightarrow \alpha + \beta + \gamma = {60^0} + {135^0} + {180^0} = {375^0}$
Hướng dẫn giải:
Sử dụng công thức tính cô sin góc giữa hai véc tơ $\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}$
