Cho $ABCD.{A_1}{B_1}{C_1}{D_1}$ là hình hộp, trong các khẳng định sau khẳng định sai:
Trả lời bởi giáo viên
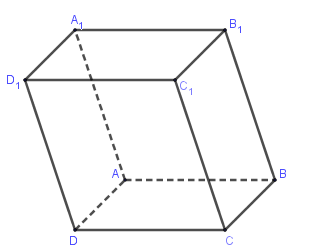
Xét đáp án A: \(\overrightarrow {A{C_1}} + \overrightarrow {{A_1}C} \)\( = \overrightarrow {AC} + \overrightarrow {C{C_1}} + \overrightarrow {{A_1}A} + \overrightarrow {AC} \) \( = 2\overrightarrow {AC} + \left( {\overrightarrow {C{C_1}} + \overrightarrow {{A_1}A} } \right) = 2\overrightarrow {AC} \) nên A đúng.
Xét đáp án B: \(\overrightarrow {A{C_1}} + \overrightarrow {C{A_1}} + 2\overrightarrow {{C_1}C} \) \( = \overrightarrow {A{C_1}} + \overrightarrow {C{A_1}} + \overrightarrow {{C_1}C} + \overrightarrow {{C_1}C} \) \( = \left( {\overrightarrow {A{C_1}} + \overrightarrow {{C_1}C} } \right) + \left( {\overrightarrow {C{A_1}} + \overrightarrow {{C_1}C} } \right)\) \( = \overrightarrow {AC} + \overrightarrow {{C_1}{A_1}} = \overrightarrow 0 \) nên B đúng.
Xét đáp án C: Do \(\overrightarrow {A{C_1}} + \overrightarrow {{A_1}C} = 2\overrightarrow {AC} \) và \(\overrightarrow {AC} \ne \overrightarrow {A{A_1}} \) nên C sai.
Xét đáp án D: \(\overrightarrow {C{A_1}} + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {C{A_1}} = \overrightarrow {A{A_1}} = \overrightarrow {C{C_1}} \) nên D đúng.
Hướng dẫn giải:
Xét tính đúng sai của từng đáp án, sử dụng quy tắc cộng véc tơ