Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều $S.ABCD$ cạnh bên $SA = 600$ mét, $\widehat {ASB} = 15^\circ $. Do có sự cố đường dây điện tại điểm $Q$ (là trung điểm của $SA$) bị hỏng, người ta tạo ra một con đường từ $A$ đến $Q$ gồm bốn đoạn thẳng: $AM$, $MN$, $NP$, $PQ$ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và có được chiều dài con đường từ $A$ đến $Q$ ngắn nhất. Tính tỉ số $k = \dfrac{{AM + MN}}{{NP + PQ}}$.
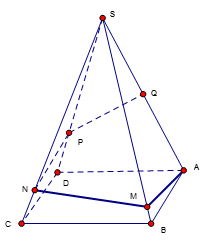
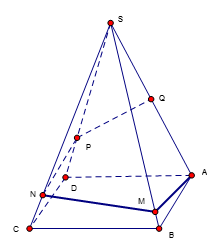
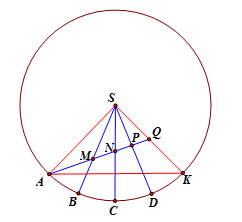
Giả sử trải các mặt hình chóp đều trên đường tròn tâm \(S\) và bán kính \(R = SA\). Ta có \(\Delta SAK\) có $\widehat {ASK} = 15^\circ .4 = 60^\circ $ $ \Rightarrow \Delta SAK$ đều.
Mà đoạn đường \(AQ\) ngắn nhất khi \(A\), \(M\), \(N\), \(P\), \(Q\) thẳng hàng.
Khi đó \(N\) là trọng tâm \(\Delta SAK\). Suy ra $k = \dfrac{{AM + MN}}{{NP + PQ}} = \dfrac{{AN}}{{NQ}} = 2$.
Cho hình lăng trụ đứng $ABC.A'B'C'$ có $AB = 1$, $AC = 2$, $AA' = 3$và $\widehat {BAC} = 120^\circ $. Gọi \(M\), \(N\) lần lượt là các điểm trên cạnh $BB'$, $CC'$sao cho $BM = 3B'M$; $CN = 2C'N$. Tính khoảng cách từ điểm \(M\) đến mặt phẳng $\left( {A'BN} \right)$.
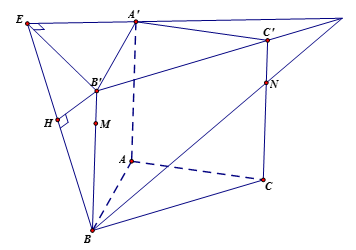
Cách 1:
Ta có \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC\cos \widehat {BAC}\) \( = {1^2} + {2^2} - 2.1.2.\cos 120^\circ = 7\). Suy ra \(BC = \sqrt 7 \).
Ta cũng có \(\cos \widehat {ABC} = \dfrac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}}\)\( = \dfrac{{{1^2} + {{\sqrt 7 }^2} - {2^2}}}{{2.1.\sqrt 7 }} = \dfrac{2}{{\sqrt 7 }}\), suy ra \(\cos \widehat {A'B'C} = \dfrac{2}{{\sqrt 7 }}\).
Gọi \(D = BN \cap B'C'\), suy ra \(\dfrac{{DC'}}{{DB'}} = \dfrac{{C'N}}{{B'B}} = \dfrac{1}{3}\), nên $DB' = \dfrac{3}{2}B'C' = \dfrac{{3\sqrt 7 }}{2}$.
Từ đó, ta có
\(A'{D^2} = A'{B'^2} + B'{D^2} - 2.A'B'.B'D.\cos \widehat {A'B'D}\)$ = {1^2} + {\left( {\dfrac{{3\sqrt 7 }}{2}} \right)^2} - 2.1.\dfrac{{3\sqrt 7 }}{2}.\dfrac{2}{{\sqrt 7 }} = \dfrac{{43}}{4}$.
Hay $A'D = \dfrac{{\sqrt {43} }}{2}$.
Kẻ \(B'E \bot A'D\) và \(B'H \bot BE\), suy ra \(B'H \bot \left( {A'BN} \right)\), do đó $d\left( {B';\left( {A'BN} \right)} \right) = B'H$.
Từ \(\cos \widehat {A'B'C} = \dfrac{2}{{\sqrt 7 }} \Rightarrow \sin \widehat {A'B'C} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}\).
Do đó ${S_{A'B'D}} = \dfrac{1}{2}.A'B'.B'D.\sin \widehat {A'B'D}$$ = \dfrac{1}{2}.1.\dfrac{{3\sqrt 7 }}{2}.\dfrac{{\sqrt 3 }}{{\sqrt 7 }} = \dfrac{{3\sqrt 3 }}{4}$.
\(B'E = \dfrac{{2{S_{A'B'D}}}}{{A'D}} = \dfrac{{2.\dfrac{{3\sqrt 3 }}{4}}}{{\dfrac{{\sqrt {43} }}{2}}} = \dfrac{{3\sqrt 3 }}{{\sqrt {43} }}\).
$\dfrac{1}{{B'{H^2}}} = \dfrac{1}{{B'{E^2}}} + \dfrac{1}{{B{{B'}^2}}}$$ = \dfrac{1}{{{{\left( {\dfrac{{3\sqrt 3 }}{{\sqrt {43} }}} \right)}^2}}} + \dfrac{1}{{{3^2}}} = \dfrac{{46}}{{27}}$\( \Rightarrow B'H = \sqrt {\dfrac{{27}}{{46}}} \).
Từ $BM = 3B'M$suy ra
$d\left( {M;\left( {A'BN} \right)} \right) = \dfrac{3}{4}d\left( {B';\left( {A'BN} \right)} \right)$$ = \dfrac{3}{4}.B'H = \dfrac{3}{4}.\sqrt {\dfrac{{27}}{{46}}} = \dfrac{{9\sqrt {138} }}{{184}}$.
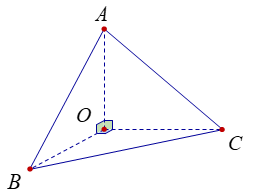
Xét tứ diện \(OABC\) có \(OA\), \(OB\), \(OC\) đôi một vuông góc. Gọi \(\alpha \), \(\beta \), \(\gamma \) lần lượt là góc giữa các đường thẳng \(OA\), \(OB\), \(OC\) với mặt phẳng \(\left( {ABC} \right)\) (hình vẽ).
Khi đó giá trị nhỏ nhất của biểu thức \(M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\) là
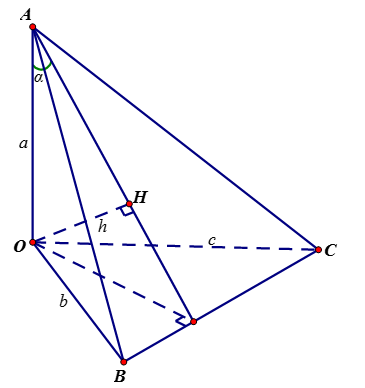
Gọi \(H\) là trực tâm tam giác \(ABC\), vì tứ diện \(OABC\) có \(OA\), \(OB\), \(OC\) đôi một vuông góc nên ta có \(OH \bot \left( {ABC} \right)\) và \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\).
Ta có \(\alpha = \widehat {\left( {OA;\left( {ABC} \right)} \right)} = \widehat {OAH}\), \(\beta = \widehat {\left( {OB;\left( {ABC} \right)} \right)} = \widehat {OBH}\), \(\gamma = \widehat {\left( {OC;\left( {ABC} \right)} \right)} = \widehat {OCH}\).
Nên \(\sin \alpha = \dfrac{{OH}}{{OA}}\), \(\sin \beta = \dfrac{{OH}}{{OB}}\), \(\sin \gamma = \dfrac{{OH}}{{OC}}\).
Đặt \(a = OA\), \(b = OB\), \(c = OC\), \(h = OH\) thì \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}\)và
\(M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)\( = \left( {2 + \dfrac{1}{{{{\sin }^2}\alpha }}} \right).\left( {2 + \dfrac{1}{{{{\sin }^2}\beta }}} \right).\left( {2 + \dfrac{1}{{{{\sin }^2}\gamma }}} \right)\)\( = \left( {2 + \dfrac{{{a^2}}}{{{h^2}}}} \right).\left( {2 + \dfrac{{{b^2}}}{{{h^2}}}} \right).\left( {2 + \dfrac{{{c^2}}}{{{h^2}}}} \right)\)\( = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right).\dfrac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\dfrac{1}{{{h^4}}} + {a^2}{b^2}{c^2}.\dfrac{1}{{{h^6}}}\).
Ta có: \(\left( {{a^2} + {b^2} + {c^2}} \right).\dfrac{1}{{{h^2}}}\)\( = \left( {{a^2} + {b^2} + {c^2}} \right).\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)\)\( \ge 3\sqrt[3]{{{a^2}.{b^2}.{c^2}}}.3\sqrt[3]{{\dfrac{1}{{{a^2}}}.\dfrac{1}{{{b^2}}}.\dfrac{1}{{{c^2}}}}} = 9\).
\(\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\dfrac{1}{{{h^4}}}\)\( = \left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)^2}\)
$ \ge 3\sqrt[3]{{{a^2}{b^2}.{b^2}{c^2}.{c^2}{a^2}}}.{\left( {3\sqrt[3]{{\left( {\dfrac{1}{{{a^2}}}.\dfrac{1}{{{b^2}}}.\dfrac{1}{{{c^2}}}} \right)}}} \right)^2}$$ = 3\sqrt[3]{{{a^4}{b^4}{c^4}}}.9\sqrt[3]{{\dfrac{1}{{{a^4}{b^4}{c^4}}}}} = 27$.
\({a^2}{b^2}{c^2}.\dfrac{1}{{{h^6}}}\)\( = {a^2}{b^2}{c^2}.{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)^3} \ge {a^2}{b^2}{c^2}.{\left( {3\sqrt[3]{{\left( {\dfrac{1}{{{a^2}}}.\dfrac{1}{{{b^2}}}.\dfrac{1}{{{c^2}}}} \right)}}} \right)^3} = 27\).
Do đó: \(M = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right).\dfrac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\dfrac{1}{{{h^4}}} + {a^2}{b^2}{c^2}.\dfrac{1}{{{h^6}}}\)
\( \ge 8 + 4.9 + 2.27 + 27 = 125\).
Dấu đẳng thức xảy ra khi và chỉ khi \(a = b = c\), hay \(OA = OB = OC\).
Vậy \(\min M = 125\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(3\). Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy. Góc giữa \(SB\) và mặt phẳng đáy bằng \(60^\circ \). Gọi \(M\), \(N\) là các điểm lần lượt thuộc cạnh đáy \(BC\) và \(CD\) sao cho \(BM = 2MC\) và \(CN = 2ND\). Tính khoảng cách giữa hai đường thẳng chéo nhau \(DM\) và \(SN.\)
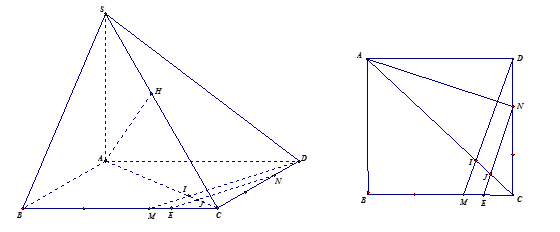
- Vì hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy nên \(SA \bot \left( {ABCD} \right)\)
\( \Rightarrow \widehat {SBA} = 60^\circ \) là góc giữa \(SB\) và mặt phẳng đáy\( \Rightarrow SA = AB.\tan 60^\circ = 3\sqrt 3 \).
- Trong mặt phẳng \(\left( {ABCD} \right)\) dựng \(NE\;{\rm{//}}\;DM\)cắt \(BC\) tại \(E\), cắt \(AC\) tại \(J\).
Gọi \(I\) là giao điểm của \(DM\) và \(AC\).
Ta có: \(DM\;{\rm{//}}\;NE \Rightarrow DM\;{\rm{//}}\;\left( {SNE} \right)\) \( \Rightarrow d\left( {DM;SN} \right) = d\left( {DM;\left( {SNE} \right)} \right) = d\left( {I;\left( {SNE} \right)} \right)\).
Do \(NE\;{\rm{//}}\;DM \Rightarrow \dfrac{{CJ}}{{CI}} = \dfrac{{CE}}{{CM}} = \dfrac{{CN}}{{CD}} = \dfrac{2}{3}\)\( \Rightarrow IJ = \dfrac{1}{3}IC\).
Lại có: \(BC\;{\rm{//}}\;AD \Rightarrow \dfrac{{IC}}{{IA}} = \dfrac{{CM}}{{AD}} = \dfrac{1}{3} \Rightarrow IC = \dfrac{1}{3}IA\)\( \Rightarrow IJ = \dfrac{1}{9}IA \Rightarrow IJ = \dfrac{1}{{10}}AJ\)
Mặt khác: \(\dfrac{{d\left( {I;\left( {SNE} \right)} \right)}}{{d\left( {A;\left( {SNE} \right)} \right)}} = \dfrac{{IJ}}{{AJ}} = \dfrac{1}{{10}}\)\( \Rightarrow d\left( {I;\left( {SNE} \right)} \right) = \dfrac{1}{{10}}d\left( {A;\left( {SNE} \right)} \right)\).
- Xét tam giác \(DAN\) và tam giác \(CDM\) có: \(DA = CD\), \(DN = CM\), \(\widehat {ADN} = \widehat {DCM} = 90^\circ \)
\( \Rightarrow \Delta DAN = \Delta CDM\) (c.g.c) \( \Rightarrow \widehat {DAN} = \widehat {CDM}\)\( \Rightarrow \widehat {DAN} + \widehat {ADM} = \widehat {CDM} + \widehat {ADM} = 90^\circ \)
\( \Rightarrow AN \bot DM \Rightarrow AN \bot NE\)\( \Rightarrow NE \bot \left( {SAN} \right) \Rightarrow \left( {SNE} \right) \bot \left( {SAN} \right)\) (có giao tuyến là \(SN\)).
- Dựng \(AH \bot SN\) tại \(H\)\( \Rightarrow AH \bot \left( {SNE} \right) \Rightarrow AH = d\left( {A;\left( {SNE} \right)} \right)\).
- Ta có: \(SA = 3\sqrt 3 \), \(AN = \sqrt {A{D^2} + D{N^2}} = \sqrt {10} \).
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{N^2}}} = \dfrac{1}{{27}} + \dfrac{1}{{10}} = \dfrac{{37}}{{270}} \Rightarrow AH = \dfrac{{3\sqrt {30} }}{{\sqrt {37} }}\)
\( \Rightarrow d\left( {DM;SN} \right) = \dfrac{1}{{10}}AH = \dfrac{{3\sqrt 3 }}{{\sqrt {370} }}\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(BC = a\), cạnh bên $SA$ vuông góc với đáy, \(SA = a\sqrt 3 \). Gọi \(M\) là trung điểm của \(AC\). Tính côtang góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\).
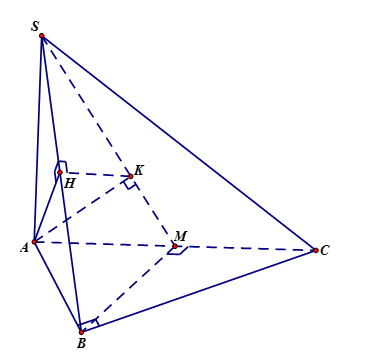
Kẻ \(AH \bot SB\) và \(AK \bot SM\).
Vì tam giác \(ABC\) vuông cân tại \(B\)và \(BC = a\)cùng với $SA \bot \left( {ABC} \right)$ nên suy ra \(BM \bot \left( {SAC} \right)\) và \(BM = AM = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\). Do đó \(BM \bot AK\).
Từ \(BM \bot AK\) và \(AK \bot SM\) suy ra \(AK \bot \left( {SBM} \right)\)\( \Rightarrow AK \bot SB\).
Từ \(AH \bot SB\) và \(AK \bot SB\) ta có \(\left( {AHK} \right) \bot SB\). Do đó, góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\) bằng hoặc bù với góc \(\widehat {AHK}\).
Ta có:
$AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }}$$ = \dfrac{{a.a\sqrt 3 }}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {a^2}} }}$$ = \dfrac{{a\sqrt 3 }}{2}$.
$AK = \dfrac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }}$$ = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a\sqrt 3 }}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}$$ = \dfrac{{a\sqrt {21} }}{7}$.
Từ \(\left( {AHK} \right) \bot SB\) ta có \(HK \bot SB\) nên \(\Delta SHK \sim \Delta SMB\), do đó \(\dfrac{{HK}}{{MB}} = \dfrac{{SK}}{{SB}}\).
Mặt khác
\(SK.SM = S{A^2}\)\( \Rightarrow SK = \dfrac{{S{A^2}}}{{SM}}\)\( = \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}\)\( = \dfrac{{3a\sqrt {14} }}{7}\);
\(SB = \sqrt {S{A^2} + A{B^2}} = 2a\);
Nên \(\dfrac{{HK}}{{MB}} = \dfrac{{SK}}{{SB}} = \dfrac{{3\sqrt {14} }}{{14}}\)\( \Rightarrow HK = \dfrac{{3\sqrt {14} }}{{14}}.MB\)\( = \dfrac{{3\sqrt {14} }}{{14}}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{3a\sqrt 7 }}{{14}}\).
Trong tam giác \(AHK\) ta có:
\(\cos \widehat {AHK} = \dfrac{{A{H^2} + H{K^2} - A{K^2}}}{{2.AH.HK}}\)\( = \dfrac{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{{3a\sqrt 7 }}{{14}}} \right)}^2} - {{\left( {\dfrac{{a\sqrt {21} }}{7}} \right)}^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{3a\sqrt 7 }}{{14}}}}\)\( = \dfrac{{\sqrt {21} }}{7}\).
Như vậy, góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\)là \(\alpha \) với \(\cos \alpha = \dfrac{{\sqrt {21} }}{7}\)\( \Rightarrow \sin \alpha = \dfrac{{2\sqrt 7 }}{7}\). Bởi vậy: \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{\sqrt 3 }}{2}\).
Cho tứ diện \(ABCD\) đều có cạnh bằng \(2\sqrt 2 \). Gọi \(G\) là trọng tâm tứ diện \(ABCD\) và \(M\) là trung điểm \(AB\). Khoảng cách giữa hai đường thẳng \(BG\) và \(CM\) bằng
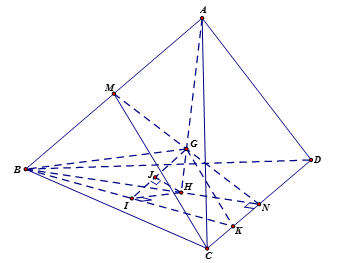
Gọi \(N\) là trung điểm \(CD\), khi đó \(G\) là trung điểm \(MN\) và \(x\) đi qua trọng tâm \(H\) của tam giác \(BCD\). Ta có \(AH \bot \left( {BCD} \right)\) và $AH = \sqrt {A{B^2} - B{H^2}} $$ = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {{\left( {\dfrac{{2\sqrt 6 }}{3}} \right)}^2}} $$ = \dfrac{{4\sqrt 3 }}{3}$.
Ta có: \(GH = \dfrac{1}{4}AH = \dfrac{{\sqrt 3 }}{3}\).
Gọi \(K\) là trung điểm \(CN\) thì \(GK{\rm{//}}CM\) nên \(CM{\rm{//}}\left( {BGK} \right)\). Do đó:
\(d\left( {BG;CM} \right) = d\left( {C;\left( {BGK} \right)} \right)\)\( = d\left( {N;\left( {BGK} \right)} \right)\)\( = \dfrac{3}{2}d\left( {H;\left( {BGK} \right)} \right)\).
Kẻ \(HI \bot BK\), \(HJ \bot GI\) với \(I \in BK\), \(J \in GI\). Khi đó \(HJ \bot \left( {BGK} \right)\) và \(HJ = d\left( {H;\left( {BGK} \right)} \right)\).
Ta có \(BK = \sqrt {B{N^2} + N{K^2}} \)\( = \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}} \)\( = \dfrac{{\sqrt {26} }}{2}\).
Ta có \(HI = BH.\sin \widehat {KBN}\) \( = BH.\dfrac{{KN}}{{BK}}\)\( = \dfrac{{2\sqrt 6 }}{3}.\dfrac{{\dfrac{{\sqrt 2 }}{2}}}{{\dfrac{{\sqrt {26} }}{2}}}\)\( = \dfrac{{2\sqrt 6 }}{{3\sqrt {13} }}\).
Do đó: \(HJ = \dfrac{{HI.HG}}{{\sqrt {H{I^2} + H{G^2}} }}\)\( = \dfrac{{\dfrac{{2\sqrt 6 }}{{3\sqrt {13} }}.\dfrac{{\sqrt 3 }}{3}}}{{\sqrt {{{\left( {\dfrac{{2\sqrt 6 }}{{3\sqrt {13} }}} \right)}^2} + {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} }}\)\( = \dfrac{{2\sqrt 2 }}{{3\sqrt 7 }}\).
Vậy \(d\left( {BG;CM} \right) = \dfrac{3}{2}d\left( {H;\left( {BGK} \right)} \right)\)\( = \dfrac{3}{2}HJ\)\( = \dfrac{3}{2}.\dfrac{{2\sqrt 2 }}{{3\sqrt 7 }}\)\( = \dfrac{2}{{\sqrt {14} }}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Số đo góc giữa hai mặt phẳng \(\left( {BA'C} \right)\) và \(\left( {DA'C} \right)\) bằng
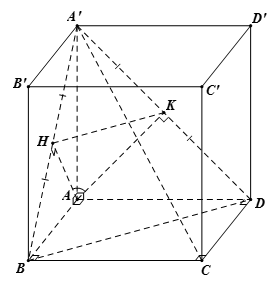
Ta có: \(AH \bot \left( {BA'C} \right),\,AK \bot \left( {DA'C} \right)\) với \(H,\,K\) lần lượt là trung điểm của \(A'B,\,A'D\)
Suy ra $\widehat {\left( {\left( {BA'C} \right);\left( {DA'C} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK}$
Lại có: \(HK\) là đường trung bình của \(\Delta A'BD\) nên \(HK = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\)
Mặt khác: \(AH = AK = \dfrac{{a\sqrt 2 }}{2}\)
Do đó \(AH = AK = HK = a\sqrt 2 \)
Suy ra \(\Delta AHK\) đều
Vậy $\widehat {\left( {\left( {BA'C} \right);\left( {DA'C} \right)} \right)} = \widehat {HAK} = 60^\circ $.
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = 2a\), \(BC = a\). Hình chiếu vuông góc \(H\) của đỉnh \(S\) trên mặt phẳng đáy là trung điểm của cạnh \(AB\), góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng \(60^\circ \). Tính cosin góc giữa hai đường thẳng \(SB\) và \(AC\)
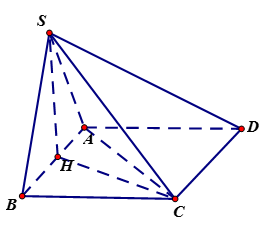
\(\left( {SC,\left( {ABCD} \right)} \right) = \)\(\left( {SC,CH} \right) = \)\(\widehat {SCH} = {60^0}\).
\(\cos \left( {SB,AC} \right) = \dfrac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } \right|}}{{SB.AC}}\)
\(\overrightarrow {SB} .\overrightarrow {AC} = \left( {\overrightarrow {SH} + \overrightarrow {HB} } \right)\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right)\)\( = \overrightarrow {SH} .\overrightarrow {AB} + \overrightarrow {SH} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \)
\( = \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \)\( = \dfrac{1}{2}A{B^2} = 2{a^2}\)
\(AC = a\sqrt 5 \), \(CH = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \), \(SH = CH.\tan \widehat {SCH} = a\sqrt 6 \).
\(SB = \sqrt {S{H^2} + H{B^2}} \)\( = \sqrt {{{\left( {a\sqrt 6 } \right)}^2} + {a^2}} = a\sqrt 7 \).
\(\cos \left( {SB,AC} \right) = \dfrac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } \right|}}{{SB.AC}}\)\( = \dfrac{{2{a^2}}}{{a\sqrt 7 .a\sqrt 5 }}\)\( = \dfrac{2}{{\sqrt {35} }}\).
Cho tứ diện \(ABCD\) có $AC = AD = BC = BD = a$ và hai mặt phẳng $\left( {ACD} \right)$, $\left( {BCD} \right)$ vuông góc với nhau. Tính độ dài cạnh \(CD\) sao cho hai mặt phẳng $\left( {ABC} \right)$, $\left( {ABD} \right)$ vuông góc.
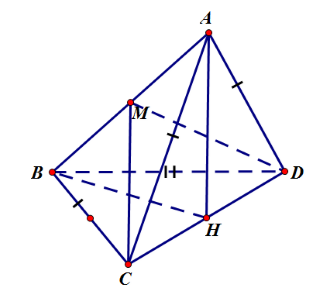
Gọi \(H\) là trung điểm của $CD$ nên \(AH \bot CD\)
\( \Leftrightarrow AH \bot \left( {BCD} \right)\) (do \(\left( {ACD} \right) \bot \left( {BCD} \right)\)) và \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\)
Gọi \(M\) là trung điểm của $AB$ nên \(CM \bot AB\)
Vì \(\left( {ABC} \right) \bot \left( {ABD} \right)\) và \(\left( {ABC} \right) \cap \left( {ABD} \right) = AB\) \( \Rightarrow CM \bot MD.\)
\(\Delta ABC = \Delta ABD\)\( \Rightarrow MC = MD\)\( \Rightarrow \Delta MCD\) vuông cân tại \(M\).
Đặt \(CD = x\) \( \Rightarrow A{H^2} = B{H^2} = {a^2} + \dfrac{{{x^2}}}{4} \Leftrightarrow A{B^2} = A{H^2} + B{H^2} = 2{a^2} + \dfrac{{{x^2}}}{2}\)
Ta có \(MH = \dfrac{1}{2}AB = \dfrac{1}{2}\sqrt {2{a^2} + \dfrac{{{x^2}}}{2}} \Leftrightarrow MH = \dfrac{{\sqrt 2 }}{2}CD \Leftrightarrow \sqrt {2{a^2} + \dfrac{{{x^2}}}{2}} .\dfrac{1}{2} = \dfrac{{\sqrt 2 }}{2}x\)
\( \Leftrightarrow 2{a^2} + \dfrac{{{x^2}}}{2} = 2{x^2} \Leftrightarrow 4{a^2} = 3{x^2} \Leftrightarrow x = \dfrac{{2a}}{{\sqrt 3 }}\).
Cho tứ diện \(ABCD\) có \(AB = 3a\), \(AC = a\sqrt {15} \), \(BD = a\sqrt {10} \), \(CD = 4a\). Biết rằng góc giữa đường thẳng \(AD\) và mặt phẳng \(\left( {BCD} \right)\) bằng \(45^\circ \), khoảng cách giữa hai đường thẳng \(AD\) và \(BC\) bằng \(\dfrac{{5a}}{4}\) và hình chiếu của \(A\) lên mặt phẳng \(\left( {BCD} \right)\) nằm trong tam giác \(BCD\). Tính độ dài đoạn thẳng \(AD\).
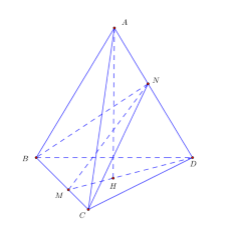
Ta xét tích vô hướng
\(\overrightarrow {AD} .\overrightarrow {BC} = \overrightarrow {AD} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)\( = \overrightarrow {AD} .\overrightarrow {AC} - \overrightarrow {AD} .\overrightarrow {AB} \)\( = = AD.AC.\cos \widehat A - AD.AB.\cos \widehat A\)\( = AD.AC.\dfrac{{A{D^2} + A{C^2} - C{D^2}}}{{2AD.AC}} - AD.AB.\dfrac{{A{D^2} + A{B^2} - B{D^2}}}{{2AD.AB}}\)\( = \dfrac{{A{D^2} + A{C^2} - C{D^2}}}{2} - \dfrac{{A{D^2} + A{B^2} - B{D^2}}}{2}\).
\( = \dfrac{{A{C^2} + B{D^2} - C{D^2} - A{B^2}}}{2}\)\( = \dfrac{{15{a^2} + 10{a^2} - 16{a^2} - 9{a^2}}}{2} = 0\)\( \Rightarrow AD \bot BC\).
Gọi \(H\) là hình chiếu của \(A\) lên mặt phẳng \(\left( {BCD} \right)\) và \(M = DH \cap BC\) suy ra \(M\) nằm giữa \(B\) và \(C\).
Ta có \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot AD\end{array} \right. \Rightarrow BC \bot \left( {AHD} \right)\)\( \Rightarrow BC \bot DM\).
Trong mặt phẳng \(\left( {ADM} \right)\) dựng \(MN \bot AD\) tại \(N\), suy ra \(\left\{ \begin{array}{l}MN \bot BC\\MN \bot AD\end{array} \right.\) suy ra \(MN\) là đoạn vuông góc chung của \(AD\) và \(BC\), do đó \(d\left( {AD;\,BC} \right) = MN = \dfrac{{5a}}{4}\).
Vì \(AH \bot \left( {BCD} \right)\) nên \(\widehat {\left( {AD;\,\left( {BCD} \right)} \right)} = \widehat {ADH} = 45^\circ \). Đồng thời \(H\) nằm giữa \(D\) và \(M\) nên \(\widehat {AMD} < 90^\circ \) suy ra \(N\) nằm giữa \(A\) và \(D\).
Ta có \(DM = MN.\sqrt 2 = \dfrac{{5a\sqrt 2 }}{4}\)\( \Rightarrow BM = \sqrt {B{D^2} - D{M^2}} = \dfrac{{a\sqrt {110} }}{4}\).
Ta có \(\left\{ \begin{array}{l}AD \bot MN\\AD \bot BC\end{array} \right. \Rightarrow AD \bot \left( {BNC} \right) \Rightarrow AD \bot BN\).
\( \Rightarrow AN = \sqrt {A{B^2} - B{N^2}} \)\( = \sqrt {A{B^2} - \left( {B{M^2} + M{N^2}} \right)} \)\( = \sqrt {9{a^2} - \left( {\dfrac{{110{a^2}}}{{16}} + \dfrac{{25{a^2}}}{{16}}} \right)} \)\( = \dfrac{{3a}}{4}\).
Mặt khác vì tam giác $DMN$ vuông cân tại \(N\) nên \(DN = MN = \dfrac{{5a}}{4}\).
Do đó \(AD = AN + DN = 2a\).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = 3$,$BC = 4$. Tam giác $SAC$ nằm trong mặt phẳng vuông góc với đáy, khoảng cách từ điểm $C$ đến đường thẳng $SA$ bằng $4$. Côsin của góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$ bằng:
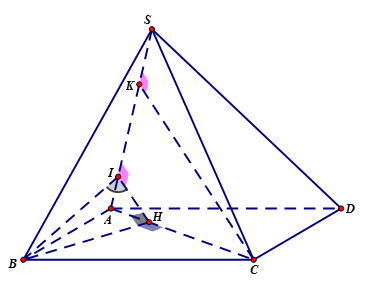
- Dựng \(BH \bot AC\) tại $H$, theo giả thiết suy ra \(BH \bot \left( {SAC} \right)\)\( \Rightarrow BH \bot SA\).
- Dựng \(HI \bot SA\) tại $I$\( \Rightarrow SA \bot \left( {BHI} \right)\)\( \Rightarrow \widehat {BIH}\) là góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$.
- Dựng \(CK \bot SA\) tại $K$ \( \Rightarrow CK = 4\) là khoảng cách từ $C$ đến $SA$.
- Ta có: \(BH = \dfrac{{BA.BC}}{{AC}}\)\( = \dfrac{{3.4}}{5} = \dfrac{{12}}{5}\)\( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \dfrac{9}{5}\).
\(IH{\rm{//}}CK\)\( \Rightarrow \dfrac{{HI}}{{CK}} = \dfrac{{AH}}{{AC}} = \dfrac{9}{{25}}\)\( \Rightarrow HI = \dfrac{9}{{25}}.CK = \dfrac{{36}}{{25}}\)
\( \Rightarrow \tan \widehat {BIH} = \dfrac{{BH}}{{HI}} = \dfrac{5}{3}\)\( \Rightarrow \cos \widehat {BIH} = \dfrac{1}{{\sqrt {1 + {{\tan }^2}\widehat {BIH}} }} = \dfrac{3}{{\sqrt {34} }}\).
Vậy \(\cos \widehat {BIH} = \dfrac{{3\sqrt {34} }}{{34}}\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, $SA \bot (ABCD)$, $SA = a\sqrt 3 $. Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM.
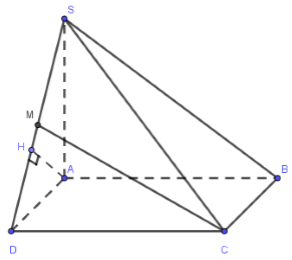
AB // CD$ \Rightarrow AB//(SCD) \supset CM$
$ \Rightarrow d\left( {AB,CM} \right) = d\left( {AB;(SCD)} \right) = d(A,(SCD))$
Kẻ $AH \bot SD,\,\,H \in SD\,\,\left( 1 \right)$ ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow SD \bot AH\,\,\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH \Rightarrow d\left( {AB,CM} \right) = AH\).
Tam giác SAD vuông tại A, $AH \bot SD,\,\,H \in SD$, suy ra:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}} = \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \Rightarrow A{H^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}$
Vậy khoảng cách giữa 2 đường thẳng CM và AB là $\dfrac{{a\sqrt 3 }}{2}$.
Cho hình chóp $S.ABC$ có góc $\widehat {ASB} = \widehat {CSB} = {60^0}$, $\widehat {ASC} = {90^0}$, $SA = a,\,\,SB = SC = 2a$. Khoảng cách d từ A đến mặt phẳng (SBC) bằng
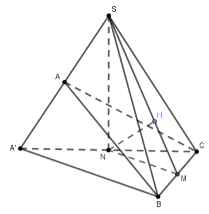
Theo đề bài, ta có: các tam giác $SAB,\,\,SBC$ có: $\widehat {ASB} = \widehat {CSB} = {60^0}$ và $SA' = \,\,SB = SC = 2a$
$ \Rightarrow \Delta SAB,\,\,\Delta SBC$ đều, cạnh bằng 2a.
$\Delta SA'C$ vuông cân tại S $ \Rightarrow A'C = SA'.\sqrt 2 = 2\sqrt 2 a$
$ \Rightarrow \Delta A'BC$ vuông cân tại B
Gọi N là trung điểm của A’C $ \Rightarrow SN \bot (A'BC)$
Gọi M là trung điểm của BC $ \Rightarrow MN//A'B$. Mà $A'B \bot BC \Rightarrow MN \bot BC \Rightarrow BC \bot (SMN)$
Ta có: $A'S \cap (SBC) = S,\,\,A'S = 2AS \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A';\left( {SBC} \right)} \right)$
Mặt khác: $A'C \cap (SBC) = C,\,\,A'C = 2NC \Rightarrow d\left( {A';\left( {SBC} \right)} \right) = 2d\left( {N;\left( {SBC} \right)} \right)$
$ \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = d\left( {N;\left( {SBC} \right)} \right)$
Trong $\left( {SMN} \right)$, kẻ $NH \bot SM \Rightarrow SM \bot (SBC) \Rightarrow d\left( {N;(SBC)} \right) = NH \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = NH$
+) Tính NH:
Ta có: $MN = \dfrac{1}{2}A'B = \dfrac{1}{2}.2a = a$(vì $\Delta SA'B$ đều, cạnh bằng 2a), $SN = \dfrac{1}{2}A'C = \dfrac{1}{2}.2\sqrt 2 a = \sqrt 2 a$ (vì $\Delta SA'C$ vuông tại S)
$\Delta SMN$ vuông tại N, $NH \bot SM \Rightarrow \dfrac{1}{{N{H^2}}} = \dfrac{1}{{S{N^2}}} + \dfrac{1}{{M{N^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{3}{{2{a^2}}} \Rightarrow NH = \dfrac{{a\sqrt 6 }}{3}$
$ \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 6 }}{3}$
Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D. \(AB = 3a;\,\,AD = DC = a.\) Gọi I là trung điểm của AD, biết hai mặt phẳng (SBI) và (SCI) vuông góc với đáy và mặt phẳng (SBC) tạo với đáy góc \({60^0}\). Tính khoảng cách từ I đến mặt phẳng (SBC).
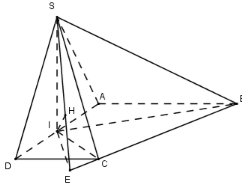
\(\left\{ \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\)
Trong (ABCD) kẻ \(IE \bot BC\) ta có
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot IE\\BC \bot SI\end{array} \right. \Rightarrow BC \bot \left( {SIE} \right) \Rightarrow BC \bot SE\\\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SE \bot BC\\\left( {ABCD} \right) \supset IE \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBCD} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {IE;SE} \right)} = \widehat {SEI} = {60^0}\end{array}\)
Trong (SIE) kẻ \(IH \bot SE \Rightarrow IH \bot BC \Rightarrow IH \bot \left( {SBC} \right) \Rightarrow d\left( {I;\left( {SBC} \right)} \right) = IH\)
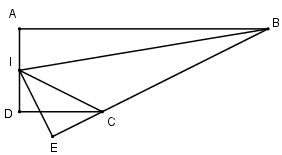
Ta có :
\(\begin{array}{l}{S_{ABI}} = \dfrac{1}{2}AB.AI = \dfrac{1}{2}3a.\dfrac{a}{2} = \dfrac{{3{a^2}}}{4}\\{S_{ICD}} = \dfrac{1}{2}CD.ID = \dfrac{1}{2}a.\dfrac{a}{2} = \dfrac{{{a^2}}}{4}\\{S_{ABCD}} = \dfrac{1}{2}AD\left( {AB + CD} \right) = \dfrac{1}{2}a\left( {a + 3a} \right) = 2{a^2}\\ \Rightarrow {S_{IBC}} = 2{a^2} - \left( {\dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{4}} \right) = {a^2}\end{array}\)
\(BC = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
Mà \({S_{IBC}} = \dfrac{1}{2}IE.BC \Leftrightarrow IE = \dfrac{{2{S_{IBC}}}}{{BC}} = \dfrac{{2{a^2}}}{{a\sqrt 5 }} = \dfrac{{2a}}{{\sqrt 5 }}\)
Xét tam giác vuông IHE có : \(IH = IE.\sin 60 = \dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt {15} }}{5}\)
Cho hình chóp S.ABC có đáy ABC là tam giác cân, AB = a, $\widehat {BAC} = {120^0}$. Gọi I là trung điểm cạnh AB. Hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy là trung điểm H của CI, góc giữa đường thẳng SA và mặt đáy bằng 600. Tính khoảng cách từ A đến mặt phẳng (SBC).
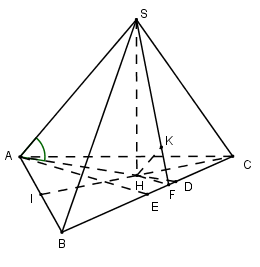
Do $\widehat {BAC} = {120^0}$ nên \(\Delta ABC\) cân tại A.
Xét tam giác ACI có \(CI = \sqrt {A{C^2} + A{I^2} - 2AC.AI.\cos {{120}^0}} = \dfrac{{a\sqrt 7 }}{2}\)
\( \Rightarrow AH = \sqrt {\dfrac{{A{C^2} + A{I^2}}}{2} - \dfrac{{C{I^2}}}{4}} = \dfrac{{a\sqrt 3 }}{4}\)
Ta có \(AH \bot \left( {ABC} \right) \Rightarrow \) HA là hình chiếu của SA trên (ABC)
\( \Rightarrow \widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {\left( {SA;HA} \right)} = \widehat {SAH} = {60^0}\)
Xét tam giác vuông SAH : \(SH = AH.\tan 60 = \dfrac{{3a}}{4}\)
Trong (ABC) kẻ \(AE \bot BC,HF \bot BC\,\,\left( {E;F \in BC} \right)\), \(D = AH \cap \left( {SBC} \right)\).
\( \Rightarrow EH\) là đường trung bình của tam giác BCI \( \Rightarrow EH = \dfrac{1}{2}BI = \dfrac{1}{4}AB = \dfrac{a}{4}\)
Ta có \(AE = AB.\sin 30 = \dfrac{a}{2}\)
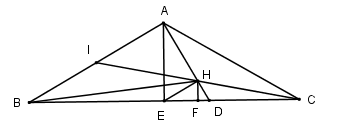
Xét tam giác AEH có : \(A{H^2} + H{E^2} = \dfrac{{{a^2}}}{4} = A{E^2} \Rightarrow \Delta AEH\) vuông tại H (Định lí Py – ta – go đảo) \( \Rightarrow AD = \dfrac{{A{E^2}}}{{AH}} = \dfrac{{a\sqrt 3 }}{3};HD = \dfrac{{E{H^2}}}{{AH}} = \dfrac{{a\sqrt 3 }}{{12}}\)
Ta có: \(AH \cap \left( {SBC} \right) = D \Rightarrow \dfrac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {H;\left( {SBC} \right)} \right)}} = \dfrac{{AD}}{{HD}} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}}}{{\dfrac{{a\sqrt 3 }}{{12}}}} = 4 \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 4d\left( {H;\left( {SBC} \right)} \right)\)
Trong (SHF) kẻ \(HK \bot SF\) ta có
\(\begin{array}{l}\left\{ \begin{array}{l}SH \bot BC\\HF \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SHF} \right) \Rightarrow BC \bot HK\\\left\{ \begin{array}{l}HK \bot BC\\HK \bot SF\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right) \Rightarrow d\left( {H;\left( {SBC} \right)} \right) = HK\end{array}\)
Ta có : \(\dfrac{{HF}}{{AE}} = \dfrac{{HD}}{{AD}} \Rightarrow HF = \dfrac{{AE.HD}}{{AD}} = \dfrac{{\dfrac{a}{2}.\dfrac{{a\sqrt 3 }}{{12}}}}{{\dfrac{{a\sqrt 3 }}{3}}} = \dfrac{a}{8}\)
\( \Rightarrow HK = \sqrt {\dfrac{{S{H^2}.H{F^2}}}{{S{H^2} + H{F^2}}}} = \sqrt {\dfrac{{{{\left( {\dfrac{{3a}}{4}} \right)}^2}.{{\left( {\dfrac{a}{8}} \right)}^2}}}{{{{\left( {\dfrac{{3a}}{4}} \right)}^2} + {{\left( {\dfrac{a}{8}} \right)}^2}}}} = \dfrac{{3a}}{{4\sqrt {37} }} \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 4HK = \dfrac{{3a}}{{\sqrt {37} }} = \dfrac{{3a\sqrt {37} }}{{37}}\)
