Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = 2a\), \(BC = a\). Hình chiếu vuông góc \(H\) của đỉnh \(S\) trên mặt phẳng đáy là trung điểm của cạnh \(AB\), góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng \(60^\circ \). Tính cosin góc giữa hai đường thẳng \(SB\) và \(AC\)
Trả lời bởi giáo viên
Đáp án đúng: b
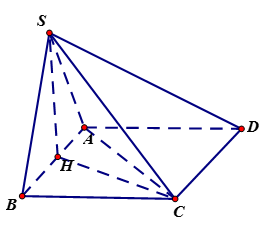
\(\left( {SC,\left( {ABCD} \right)} \right) = \)\(\left( {SC,CH} \right) = \)\(\widehat {SCH} = {60^0}\).
\(\cos \left( {SB,AC} \right) = \dfrac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } \right|}}{{SB.AC}}\)
\(\overrightarrow {SB} .\overrightarrow {AC} = \left( {\overrightarrow {SH} + \overrightarrow {HB} } \right)\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right)\)\( = \overrightarrow {SH} .\overrightarrow {AB} + \overrightarrow {SH} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \)
\( = \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \)\( = \dfrac{1}{2}A{B^2} = 2{a^2}\)
\(AC = a\sqrt 5 \), \(CH = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \), \(SH = CH.\tan \widehat {SCH} = a\sqrt 6 \).
\(SB = \sqrt {S{H^2} + H{B^2}} \)\( = \sqrt {{{\left( {a\sqrt 6 } \right)}^2} + {a^2}} = a\sqrt 7 \).
\(\cos \left( {SB,AC} \right) = \dfrac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } \right|}}{{SB.AC}}\)\( = \dfrac{{2{a^2}}}{{a\sqrt 7 .a\sqrt 5 }}\)\( = \dfrac{2}{{\sqrt {35} }}\).
Hướng dẫn giải:
Sử dụng phương pháp véc tơ: \(\cos \left( {SB,AC} \right) = \dfrac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } \right|}}{{SB.AC}}\)
Tính \(\overrightarrow {SB} .\overrightarrow {AC} \) và các độ dài \(SB,AC\) rồi suy ra đáp số.
