Câu hỏi:
2 năm trước
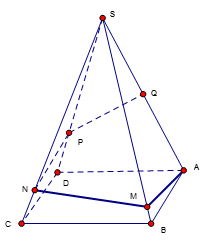
Cho hình lăng trụ đứng $ABC.A'B'C'$ có $AB = 1$, $AC = 2$, $AA' = 3$và $\widehat {BAC} = 120^\circ $. Gọi \(M\), \(N\) lần lượt là các điểm trên cạnh $BB'$, $CC'$sao cho $BM = 3B'M$; $CN = 2C'N$. Tính khoảng cách từ điểm \(M\) đến mặt phẳng $\left( {A'BN} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: a
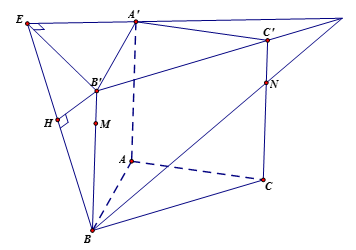
Cách 1:
Ta có \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC\cos \widehat {BAC}\) \( = {1^2} + {2^2} - 2.1.2.\cos 120^\circ = 7\). Suy ra \(BC = \sqrt 7 \).
Ta cũng có \(\cos \widehat {ABC} = \dfrac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}}\)\( = \dfrac{{{1^2} + {{\sqrt 7 }^2} - {2^2}}}{{2.1.\sqrt 7 }} = \dfrac{2}{{\sqrt 7 }}\), suy ra \(\cos \widehat {A'B'C} = \dfrac{2}{{\sqrt 7 }}\).
Gọi \(D = BN \cap B'C'\), suy ra \(\dfrac{{DC'}}{{DB'}} = \dfrac{{C'N}}{{B'B}} = \dfrac{1}{3}\), nên $DB' = \dfrac{3}{2}B'C' = \dfrac{{3\sqrt 7 }}{2}$.
Từ đó, ta có
\(A'{D^2} = A'{B'^2} + B'{D^2} - 2.A'B'.B'D.\cos \widehat {A'B'D}\)$ = {1^2} + {\left( {\dfrac{{3\sqrt 7 }}{2}} \right)^2} - 2.1.\dfrac{{3\sqrt 7 }}{2}.\dfrac{2}{{\sqrt 7 }} = \dfrac{{43}}{4}$.
Hay $A'D = \dfrac{{\sqrt {43} }}{2}$.
Kẻ \(B'E \bot A'D\) và \(B'H \bot BE\), suy ra \(B'H \bot \left( {A'BN} \right)\), do đó $d\left( {B';\left( {A'BN} \right)} \right) = B'H$.
Từ \(\cos \widehat {A'B'C} = \dfrac{2}{{\sqrt 7 }} \Rightarrow \sin \widehat {A'B'C} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}\).
Do đó ${S_{A'B'D}} = \dfrac{1}{2}.A'B'.B'D.\sin \widehat {A'B'D}$$ = \dfrac{1}{2}.1.\dfrac{{3\sqrt 7 }}{2}.\dfrac{{\sqrt 3 }}{{\sqrt 7 }} = \dfrac{{3\sqrt 3 }}{4}$.
\(B'E = \dfrac{{2{S_{A'B'D}}}}{{A'D}} = \dfrac{{2.\dfrac{{3\sqrt 3 }}{4}}}{{\dfrac{{\sqrt {43} }}{2}}} = \dfrac{{3\sqrt 3 }}{{\sqrt {43} }}\).
$\dfrac{1}{{B'{H^2}}} = \dfrac{1}{{B'{E^2}}} + \dfrac{1}{{B{{B'}^2}}}$$ = \dfrac{1}{{{{\left( {\dfrac{{3\sqrt 3 }}{{\sqrt {43} }}} \right)}^2}}} + \dfrac{1}{{{3^2}}} = \dfrac{{46}}{{27}}$\( \Rightarrow B'H = \sqrt {\dfrac{{27}}{{46}}} \).
Từ $BM = 3B'M$suy ra
$d\left( {M;\left( {A'BN} \right)} \right) = \dfrac{3}{4}d\left( {B';\left( {A'BN} \right)} \right)$$ = \dfrac{3}{4}.B'H = \dfrac{3}{4}.\sqrt {\dfrac{{27}}{{46}}} = \dfrac{{9\sqrt {138} }}{{184}}$.
Hướng dẫn giải:
- Nhận xét $d\left( {M;\left( {A'BN} \right)} \right) = \dfrac{3}{4}d\left( {B';\left( {A'BN} \right)} \right)$
- Từ đó tính khoảng cách $d\left( {B';\left( {A'BN} \right)} \right)$ bằng cách dựng \(H\) là hình chiếu của \(B'\) trên \(\left( {A'BN} \right)\)
- Tính độ dài \(B'H\) và suy ra khoảng cách cần tìm.
