Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Số đo góc giữa hai mặt phẳng \(\left( {BA'C} \right)\) và \(\left( {DA'C} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
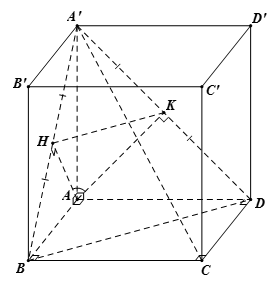
Ta có: \(AH \bot \left( {BA'C} \right),\,AK \bot \left( {DA'C} \right)\) với \(H,\,K\) lần lượt là trung điểm của \(A'B,\,A'D\)
Suy ra $\widehat {\left( {\left( {BA'C} \right);\left( {DA'C} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK}$
Lại có: \(HK\) là đường trung bình của \(\Delta A'BD\) nên \(HK = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\)
Mặt khác: \(AH = AK = \dfrac{{a\sqrt 2 }}{2}\)
Do đó \(AH = AK = HK = a\sqrt 2 \)
Suy ra \(\Delta AHK\) đều
Vậy $\widehat {\left( {\left( {BA'C} \right);\left( {DA'C} \right)} \right)} = \widehat {HAK} = 60^\circ $.
Hướng dẫn giải:
Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
