Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(3\). Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy. Góc giữa \(SB\) và mặt phẳng đáy bằng \(60^\circ \). Gọi \(M\), \(N\) là các điểm lần lượt thuộc cạnh đáy \(BC\) và \(CD\) sao cho \(BM = 2MC\) và \(CN = 2ND\). Tính khoảng cách giữa hai đường thẳng chéo nhau \(DM\) và \(SN.\)

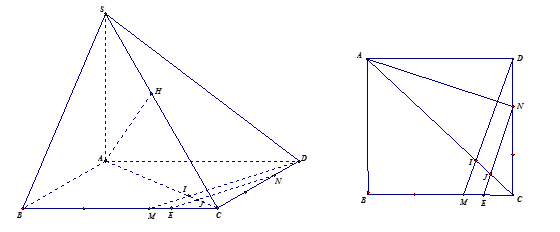
- Vì hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy nên \(SA \bot \left( {ABCD} \right)\)

\( \Rightarrow \widehat {SBA} = 60^\circ \) là góc giữa \(SB\) và mặt phẳng đáy\( \Rightarrow SA = AB.\tan 60^\circ  = 3\sqrt 3 \).

- Trong mặt phẳng \(\left( {ABCD} \right)\) dựng \(NE\;{\rm{//}}\;DM\)cắt \(BC\) tại \(E\), cắt \(AC\) tại \(J\).

Gọi \(I\) là giao điểm của \(DM\) và \(AC\).

Ta có: \(DM\;{\rm{//}}\;NE \Rightarrow DM\;{\rm{//}}\;\left( {SNE} \right)\) \( \Rightarrow d\left( {DM;SN} \right) = d\left( {DM;\left( {SNE} \right)} \right) = d\left( {I;\left( {SNE} \right)} \right)\).

Do \(NE\;{\rm{//}}\;DM \Rightarrow \dfrac{{CJ}}{{CI}} = \dfrac{{CE}}{{CM}} = \dfrac{{CN}}{{CD}} = \dfrac{2}{3}\)\( \Rightarrow IJ = \dfrac{1}{3}IC\).

Lại có: \(BC\;{\rm{//}}\;AD \Rightarrow \dfrac{{IC}}{{IA}} = \dfrac{{CM}}{{AD}} = \dfrac{1}{3} \Rightarrow IC = \dfrac{1}{3}IA\)\( \Rightarrow IJ = \dfrac{1}{9}IA \Rightarrow IJ = \dfrac{1}{{10}}AJ\)

Mặt khác: \(\dfrac{{d\left( {I;\left( {SNE} \right)} \right)}}{{d\left( {A;\left( {SNE} \right)} \right)}} = \dfrac{{IJ}}{{AJ}} = \dfrac{1}{{10}}\)\( \Rightarrow d\left( {I;\left( {SNE} \right)} \right) = \dfrac{1}{{10}}d\left( {A;\left( {SNE} \right)} \right)\).

- Xét tam giác \(DAN\) và tam giác \(CDM\) có: \(DA = CD\), \(DN = CM\), \(\widehat {ADN} = \widehat {DCM} = 90^\circ \)

\( \Rightarrow \Delta DAN = \Delta CDM\) (c.g.c) \( \Rightarrow \widehat {DAN} = \widehat {CDM}\)\( \Rightarrow \widehat {DAN} + \widehat {ADM} = \widehat {CDM} + \widehat {ADM} = 90^\circ \)

\( \Rightarrow AN \bot DM \Rightarrow AN \bot NE\)\( \Rightarrow NE \bot \left( {SAN} \right) \Rightarrow \left( {SNE} \right) \bot \left( {SAN} \right)\) (có giao tuyến là \(SN\)).

- Dựng \(AH \bot SN\) tại \(H\)\( \Rightarrow AH \bot \left( {SNE} \right) \Rightarrow AH = d\left( {A;\left( {SNE} \right)} \right)\).

- Ta có: \(SA = 3\sqrt 3 \), \(AN = \sqrt {A{D^2} + D{N^2}}  = \sqrt {10} \).

\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{N^2}}} = \dfrac{1}{{27}} + \dfrac{1}{{10}} = \dfrac{{37}}{{270}} \Rightarrow AH = \dfrac{{3\sqrt {30} }}{{\sqrt {37} }}\)

\( \Rightarrow d\left( {DM;SN} \right) = \dfrac{1}{{10}}AH = \dfrac{{3\sqrt 3 }}{{\sqrt {370} }}\).