Xét tứ diện \(OABC\) có \(OA\), \(OB\), \(OC\) đôi một vuông góc. Gọi \(\alpha \), \(\beta \), \(\gamma \) lần lượt là góc giữa các đường thẳng \(OA\), \(OB\), \(OC\) với mặt phẳng \(\left( {ABC} \right)\) (hình vẽ).

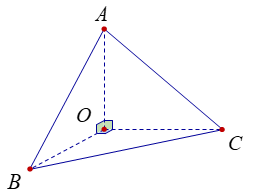
Khi đó giá trị nhỏ nhất của biểu thức \(M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\) là

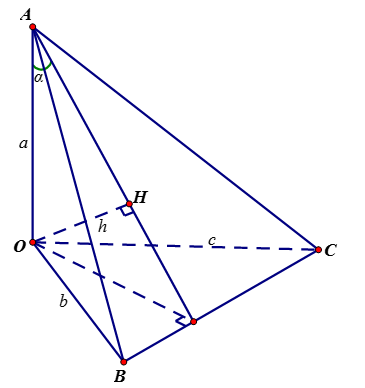
Gọi \(H\) là trực tâm tam giác \(ABC\), vì tứ diện \(OABC\) có \(OA\), \(OB\), \(OC\) đôi một vuông góc nên ta có \(OH \bot \left( {ABC} \right)\) và \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\).

Ta có \(\alpha  = \widehat {\left( {OA;\left( {ABC} \right)} \right)} = \widehat {OAH}\), \(\beta  = \widehat {\left( {OB;\left( {ABC} \right)} \right)} = \widehat {OBH}\), \(\gamma  = \widehat {\left( {OC;\left( {ABC} \right)} \right)} = \widehat {OCH}\).

Nên \(\sin \alpha  = \dfrac{{OH}}{{OA}}\), \(\sin \beta  = \dfrac{{OH}}{{OB}}\), \(\sin \gamma  = \dfrac{{OH}}{{OC}}\).

Đặt \(a = OA\), \(b = OB\), \(c = OC\), \(h = OH\) thì \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}\)và

\(M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)\( = \left( {2 + \dfrac{1}{{{{\sin }^2}\alpha }}} \right).\left( {2 + \dfrac{1}{{{{\sin }^2}\beta }}} \right).\left( {2 + \dfrac{1}{{{{\sin }^2}\gamma }}} \right)\)\( = \left( {2 + \dfrac{{{a^2}}}{{{h^2}}}} \right).\left( {2 + \dfrac{{{b^2}}}{{{h^2}}}} \right).\left( {2 + \dfrac{{{c^2}}}{{{h^2}}}} \right)\)\( = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right).\dfrac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\dfrac{1}{{{h^4}}} + {a^2}{b^2}{c^2}.\dfrac{1}{{{h^6}}}\).

Ta có: \(\left( {{a^2} + {b^2} + {c^2}} \right).\dfrac{1}{{{h^2}}}\)\( = \left( {{a^2} + {b^2} + {c^2}} \right).\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)\)\( \ge 3\sqrt[3]{{{a^2}.{b^2}.{c^2}}}.3\sqrt[3]{{\dfrac{1}{{{a^2}}}.\dfrac{1}{{{b^2}}}.\dfrac{1}{{{c^2}}}}} = 9\).

\(\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\dfrac{1}{{{h^4}}}\)\( = \left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)^2}\)

$ \ge 3\sqrt[3]{{{a^2}{b^2}.{b^2}{c^2}.{c^2}{a^2}}}.{\left( {3\sqrt[3]{{\left( {\dfrac{1}{{{a^2}}}.\dfrac{1}{{{b^2}}}.\dfrac{1}{{{c^2}}}} \right)}}} \right)^2}$$ = 3\sqrt[3]{{{a^4}{b^4}{c^4}}}.9\sqrt[3]{{\dfrac{1}{{{a^4}{b^4}{c^4}}}}} = 27$.

\({a^2}{b^2}{c^2}.\dfrac{1}{{{h^6}}}\)\( = {a^2}{b^2}{c^2}.{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)^3} \ge {a^2}{b^2}{c^2}.{\left( {3\sqrt[3]{{\left( {\dfrac{1}{{{a^2}}}.\dfrac{1}{{{b^2}}}.\dfrac{1}{{{c^2}}}} \right)}}} \right)^3} = 27\).

Do đó: \(M = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right).\dfrac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\dfrac{1}{{{h^4}}} + {a^2}{b^2}{c^2}.\dfrac{1}{{{h^6}}}\)

\( \ge 8 + 4.9 + 2.27 + 27 = 125\).

Dấu đẳng thức xảy ra khi và chỉ khi \(a = b = c\), hay \(OA = OB = OC\).

Vậy \(\min M = 125\).