Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) đều có cạnh bằng \(2\sqrt 2 \). Gọi \(G\) là trọng tâm tứ diện \(ABCD\) và \(M\) là trung điểm \(AB\). Khoảng cách giữa hai đường thẳng \(BG\) và \(CM\) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
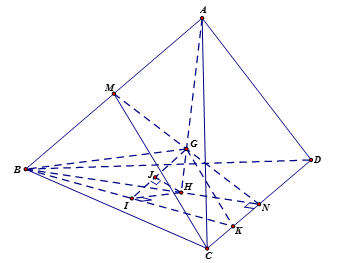
Gọi \(N\) là trung điểm \(CD\), khi đó \(G\) là trung điểm \(MN\) và \(x\) đi qua trọng tâm \(H\) của tam giác \(BCD\). Ta có \(AH \bot \left( {BCD} \right)\) và $AH = \sqrt {A{B^2} - B{H^2}} $$ = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {{\left( {\dfrac{{2\sqrt 6 }}{3}} \right)}^2}} $$ = \dfrac{{4\sqrt 3 }}{3}$.
Ta có: \(GH = \dfrac{1}{4}AH = \dfrac{{\sqrt 3 }}{3}\).
Gọi \(K\) là trung điểm \(CN\) thì \(GK{\rm{//}}CM\) nên \(CM{\rm{//}}\left( {BGK} \right)\). Do đó:
\(d\left( {BG;CM} \right) = d\left( {C;\left( {BGK} \right)} \right)\)\( = d\left( {N;\left( {BGK} \right)} \right)\)\( = \dfrac{3}{2}d\left( {H;\left( {BGK} \right)} \right)\).
Kẻ \(HI \bot BK\), \(HJ \bot GI\) với \(I \in BK\), \(J \in GI\). Khi đó \(HJ \bot \left( {BGK} \right)\) và \(HJ = d\left( {H;\left( {BGK} \right)} \right)\).
Ta có \(BK = \sqrt {B{N^2} + N{K^2}} \)\( = \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}} \)\( = \dfrac{{\sqrt {26} }}{2}\).
Ta có \(HI = BH.\sin \widehat {KBN}\) \( = BH.\dfrac{{KN}}{{BK}}\)\( = \dfrac{{2\sqrt 6 }}{3}.\dfrac{{\dfrac{{\sqrt 2 }}{2}}}{{\dfrac{{\sqrt {26} }}{2}}}\)\( = \dfrac{{2\sqrt 6 }}{{3\sqrt {13} }}\).
Do đó: \(HJ = \dfrac{{HI.HG}}{{\sqrt {H{I^2} + H{G^2}} }}\)\( = \dfrac{{\dfrac{{2\sqrt 6 }}{{3\sqrt {13} }}.\dfrac{{\sqrt 3 }}{3}}}{{\sqrt {{{\left( {\dfrac{{2\sqrt 6 }}{{3\sqrt {13} }}} \right)}^2} + {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} }}\)\( = \dfrac{{2\sqrt 2 }}{{3\sqrt 7 }}\).
Vậy \(d\left( {BG;CM} \right) = \dfrac{3}{2}d\left( {H;\left( {BGK} \right)} \right)\)\( = \dfrac{3}{2}HJ\)\( = \dfrac{3}{2}.\dfrac{{2\sqrt 2 }}{{3\sqrt 7 }}\)\( = \dfrac{2}{{\sqrt {14} }}\).
Hướng dẫn giải:
- Gọi \(N\) là trung điểm \(CD,\) \(K\) là trung điểm \(CN\) \( \Rightarrow d\left( {BG;CM} \right) = d\left( {C;\left( {BGK} \right)} \right)\)\( = d\left( {N;\left( {BGK} \right)} \right)\)
- Tính khoảng cách trên và suy ra kết luận.
