Cho tứ diện \(ABCD\) có \(AB = 3a\), \(AC = a\sqrt {15} \), \(BD = a\sqrt {10} \), \(CD = 4a\). Biết rằng góc giữa đường thẳng \(AD\) và mặt phẳng \(\left( {BCD} \right)\) bằng \(45^\circ \), khoảng cách giữa hai đường thẳng \(AD\) và \(BC\) bằng \(\dfrac{{5a}}{4}\) và hình chiếu của \(A\) lên mặt phẳng \(\left( {BCD} \right)\) nằm trong tam giác \(BCD\). Tính độ dài đoạn thẳng \(AD\).
Trả lời bởi giáo viên
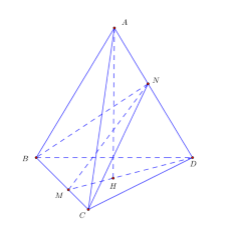
Ta xét tích vô hướng
\(\overrightarrow {AD} .\overrightarrow {BC} = \overrightarrow {AD} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)\( = \overrightarrow {AD} .\overrightarrow {AC} - \overrightarrow {AD} .\overrightarrow {AB} \)\( = = AD.AC.\cos \widehat A - AD.AB.\cos \widehat A\)\( = AD.AC.\dfrac{{A{D^2} + A{C^2} - C{D^2}}}{{2AD.AC}} - AD.AB.\dfrac{{A{D^2} + A{B^2} - B{D^2}}}{{2AD.AB}}\)\( = \dfrac{{A{D^2} + A{C^2} - C{D^2}}}{2} - \dfrac{{A{D^2} + A{B^2} - B{D^2}}}{2}\).
\( = \dfrac{{A{C^2} + B{D^2} - C{D^2} - A{B^2}}}{2}\)\( = \dfrac{{15{a^2} + 10{a^2} - 16{a^2} - 9{a^2}}}{2} = 0\)\( \Rightarrow AD \bot BC\).
Gọi \(H\) là hình chiếu của \(A\) lên mặt phẳng \(\left( {BCD} \right)\) và \(M = DH \cap BC\) suy ra \(M\) nằm giữa \(B\) và \(C\).
Ta có \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot AD\end{array} \right. \Rightarrow BC \bot \left( {AHD} \right)\)\( \Rightarrow BC \bot DM\).
Trong mặt phẳng \(\left( {ADM} \right)\) dựng \(MN \bot AD\) tại \(N\), suy ra \(\left\{ \begin{array}{l}MN \bot BC\\MN \bot AD\end{array} \right.\) suy ra \(MN\) là đoạn vuông góc chung của \(AD\) và \(BC\), do đó \(d\left( {AD;\,BC} \right) = MN = \dfrac{{5a}}{4}\).
Vì \(AH \bot \left( {BCD} \right)\) nên \(\widehat {\left( {AD;\,\left( {BCD} \right)} \right)} = \widehat {ADH} = 45^\circ \). Đồng thời \(H\) nằm giữa \(D\) và \(M\) nên \(\widehat {AMD} < 90^\circ \) suy ra \(N\) nằm giữa \(A\) và \(D\).
Ta có \(DM = MN.\sqrt 2 = \dfrac{{5a\sqrt 2 }}{4}\)\( \Rightarrow BM = \sqrt {B{D^2} - D{M^2}} = \dfrac{{a\sqrt {110} }}{4}\).
Ta có \(\left\{ \begin{array}{l}AD \bot MN\\AD \bot BC\end{array} \right. \Rightarrow AD \bot \left( {BNC} \right) \Rightarrow AD \bot BN\).
\( \Rightarrow AN = \sqrt {A{B^2} - B{N^2}} \)\( = \sqrt {A{B^2} - \left( {B{M^2} + M{N^2}} \right)} \)\( = \sqrt {9{a^2} - \left( {\dfrac{{110{a^2}}}{{16}} + \dfrac{{25{a^2}}}{{16}}} \right)} \)\( = \dfrac{{3a}}{4}\).
Mặt khác vì tam giác $DMN$ vuông cân tại \(N\) nên \(DN = MN = \dfrac{{5a}}{4}\).
Do đó \(AD = AN + DN = 2a\).
Hướng dẫn giải:
- Xác định đoạn vuông góc chung của \(AD,BC\)
- Xác định góc \({45^0}\) và sử dụng các kiến thức hình học đã biết tính độ dài \(AD\)