Bài toán tìm giao điểm của đường thẳng và mặt phẳng

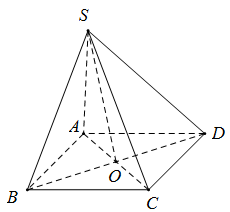
Ta có $AC \subset \left( {ABCD} \right)$

$\left( {ABCD} \right) \cap \left( {SBD} \right) = BD$

Giao điểm của $BD$  và $AC$ là $O$

$\Rightarrow O$  là giao điểm của $AC$  và mặt phẳng $\left( {SBD} \right)$

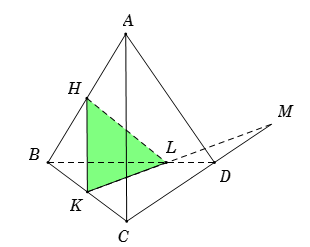
Ta có $HK$, $KM$ là đoạn giao tuyến của $\left( {HKM} \right)$ với $\left( {ABC} \right)$ và $\left( {BCD} \right)$.

Trong  mặt  phẳng $\left( {BCD} \right)$,  do $KM$ không  song song với $BD$ nên gọi $L = KM \cap BD$.

Vậy thiết diện là tam giác $HKL$.

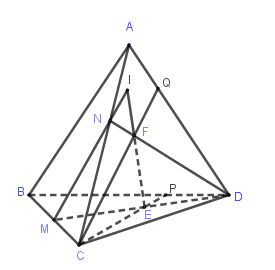
Ta có $EF \subset \left( {DEF} \right) \Rightarrow EF \subset \left( {DMN} \right)$

$\left( {DMN} \right) \cap \left( {ABC} \right) = MN$

Gọi $I$ là giao điểm của $EF$ và $MN$

$⇒ I$ là giao của $EF$ và $(ABC)$

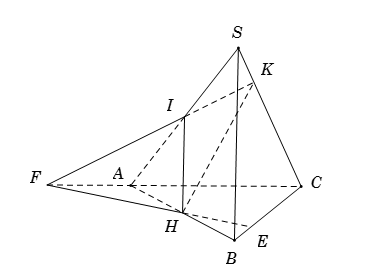
+) Chọn mặt phẳng phụ $\left( {ABC} \right)$ chứa $BC$.

+) Tìm giao tuyến của hai mặt phẳng $\left( {ABC} \right)$ và $\left( {IHK} \right)$.

Ta có $H$ là điểm chung thứ nhất của $\left( {ABC} \right)$ và $\left( {IHK} \right)$.

Trong mặt phẳng $\left( {SAC} \right)$, do $IK$ không song song với $AC$ nên gọi $F = IK \cap AC$. Ta có

        ▪ $F \in AC$ mà $AC \subset \left( {ABC} \right)$ suy ra $F \in \left( {ABC} \right)$.

        ▪ $F \in IK$ mà $IK \subset \left( {IHK} \right)$ suy ra $F \in \left( {IHK} \right)$.

Suy ra $F$ là điểm chung thứ hai của $\left( {ABC} \right)$ và $\left( {IHK} \right)$.

Do đó $\left( {ABC} \right) \cap \left( {IHK} \right) = HF$.

+) Trong mặt phẳng $\left( {ABC} \right)$, gọi $E = HF \cap BC$. Ta có

        ▪ $E \in HF$ mà $HF \subset \left( {IHK} \right)$ suy ra $E \in \left( {IHK} \right)$.

        ▪ $E \in BC$.

Vậy $E = BC \cap \left( {IHK} \right)$.

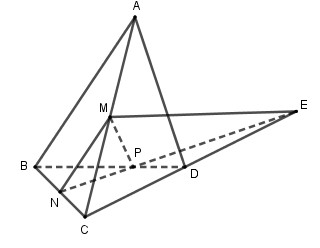
Cách 1. Xét mặt phẳng $\left( {BCD} \right)$ chứa $CD\,.$

Do $NP$ không song song $CD$ nên $NP$ cắt $CD$ tại $E\,.$

Điểm $E \in NP\,\, \Rightarrow \,\,E \in \left( {MNP} \right).$ Vậy $CD \cap \left( {MNP} \right)$ tại $E.$

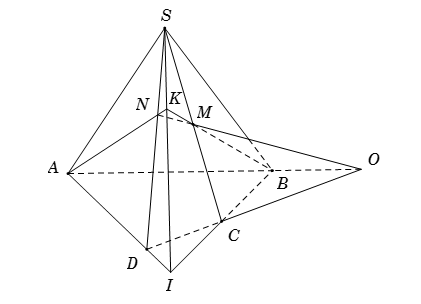
Gọi $I = AD \cap BC.$ Trong mặt phẳng $\left( {SBC} \right)$, gọi $K = BM \cap SI$. Trong mặt phẳng $\left( {SAD} \right)$, gọi $N = AK \cap SD$.

Khi đó $N$ là giao điểm của đường thẳng $SD$ với mặt phẳng $\left( {AMB} \right)$.

Gọi $O = AB \cap CD$. Ta có:

• $O \in AB$ mà $AB \subset \left( {AMB} \right)$ suy ra $O \in \left( {AMB} \right)$.
• $O \in CD$ mà $CD \subset \left( {SCD} \right)$ suy ra ${\rm{IJ}},MN,SE$.

Do đó $O \in \left( {AMB} \right) \cap \left( {SCD} \right)$.    $\left( 1 \right)$

Mà $\left( {AMB} \right) \cap \left( {SCD} \right) = MN$.   $\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$, suy ra $O \in MN$. Vậy ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ đồng quy.

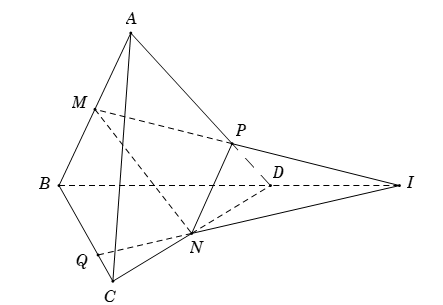
Ta có $\left( {ABD} \right) \cap \left( {BCD} \right) = BD$.

Lại có $\left\{ \begin{array}{l}I \in MP \subset \left( {ABD} \right)\\I \in NQ \subset \left( {BCD} \right)\end{array} \right. \Rightarrow I$ thuộc giao tuyến của $\left( {ABD} \right)$ và $\left( {BCD} \right)$

$\Rightarrow I \in BD \Rightarrow I,{\rm{ }}B,{\rm{ }}D$ thẳng hàng.

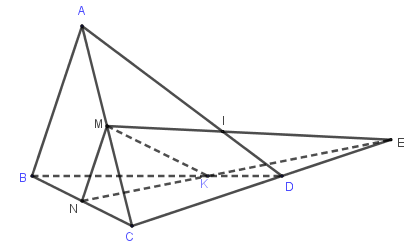
Vì $I$ là giao của $AD$ và $\left( {MNK} \right)$ nên $I \in \left( {MNK} \right)$

$\Rightarrow MI \subset \left( {MNK} \right)$

Mà $E \in MI \Rightarrow E \in \left( {MNK} \right)$

$\Rightarrow E$  thuộc giao tuyến của $\left( {MNK} \right)$ và $\left( {BCD} \right)$

$\Rightarrow E \in NK$

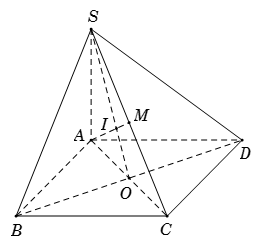
Gọi $O$ là tâm hình bình hành $ABCD$ suy ra $O$ là trung điểm của $AC\,.$

Nối $AM$ cắt $SO$ tại $I$ mà $SO \subset \left( {SBD} \right)$ suy ra $I = AM \cap \left( {SBD} \right).$

Tam giác $SAC$ có $M,\,\,O$ lần lượt là trung điểm của $SC,\,\,AC.$

Mà $I = AM \cap SO$ suy ra $I$ là trọng tâm tam giác $SAC\,\, \Rightarrow \,\,AI = \dfrac{2}{3}AM\,\, \Leftrightarrow \,\,IA = 2IM.$

Điểm $I$ nằm giữa $A$ và $M$ suy ra $\overrightarrow {IA}  = 2\overrightarrow {MI}  =  - \,2\overrightarrow {IM} .$

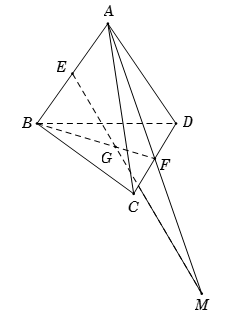
Vì $G$ là trọng tâm tam giác $BCD,\,\,\,F$ là trung điểm của $CD$$\Rightarrow \,\,\,G \in \left( {ABF} \right)\,.$

Ta có $E$ là trung điểm của $AB$$\Rightarrow \,\,\,E \in \left( {ABF} \right)\,.$

Trong $\left( {ABF} \right)$, gọi $M$ là giao điểm của $EG$ và $AF$ mà $AF \subset \left( {ACD} \right)$ suy ra $M \in \left( {ACD} \right)\,.$

Vậy giao điểm của $EG$ và $mp\,\,\left( {ACD} \right)$ là giao điểm $M = EG \cap AF\,.$

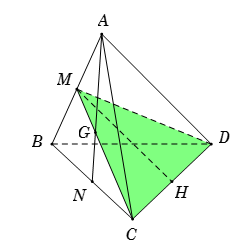
Gọi $M,\,\,N$ lần lượt là trung điểm của $AB,\,\,BC$ suy ra $AN \cap MC = G.$

Dễ thấy mặt phẳng $\left( {GCD} \right)$ cắt đường thắng $AB$ tại điểm $M.$

Suy ra tam giác $MCD$ là thiết diện của mặt phẳng $\left( {GCD} \right)$ và tứ diện $ABCD\,.$

Tam giác $ABD$ đều, có $M$ là trung điểm $AB$ suy ra $MD = \dfrac{{a\sqrt 3 }}{2}.$

Tam giác $ABC$đều, có $M$ là trung điểm $AB$ suy ra $MC = \dfrac{{a\sqrt 3 }}{2}.$

Gọi $H$ là trung điểm của $CD\,\, \Rightarrow \,\,MH \bot CD\,\, \Rightarrow \,\,{S_{\Delta MCD}} = \dfrac{1}{2}.MH.CD$

Với $MH = \sqrt {M{C^2} - H{C^2}}  = \sqrt {M{C^2} - \dfrac{{C{D^2}}}{4}}  = \dfrac{{a\sqrt 2 }}{2}.$

Vậy ${S_{\Delta MCD}} = \dfrac{1}{2}.\dfrac{{a\sqrt 2 }}{2}.a = \dfrac{{{a^2}\sqrt 2 }}{4}\,.$

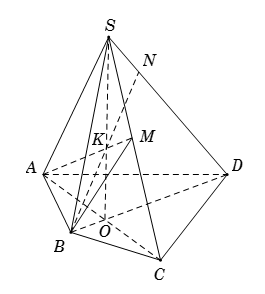
Chọn mặt phẳng phụ $\left( {SBD} \right)$ chứa $SD$.

Tìm giao tuyến của hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABM} \right)$.

Ta có $B$ là điểm chung thứ nhất của $\left( {SBD} \right)$ và $\left( {ABM} \right)$.

Trong mặt phẳng $\left( {ABCD} \right)$, gọi $O = AC \cap BD$. Trong mặt phẳng $\left( {SAC} \right)$, gọi $K = AM \cap SO$. Ta có:

        ▪ $K \in SO$ mà $SO \subset \left( {SBD} \right)$ suy ra $K \in \left( {SBD} \right)$.

        ▪ $K \in AM$ mà $AM \subset \left( {ABM} \right)$ suy ra $K \in \left( {ABM} \right)$.

Suy ra $K$ là điểm chung thứ hai của $\left( {SBD} \right)$ và $\left( {ABM} \right)$.

Do đó $\left( {SBD} \right) \cap \left( {ABM} \right) = BK$.

• Trong mặt phẳng $\left( {SBD} \right)$, gọi $N = SD \cap BK$. Ta có:

        ▪ $N \in BK$ mà $BK \subset \left( {ABM} \right)$ suy ra $N \in \left( {ABM} \right)$.

        ▪ $N \in SD$.

Vậy $N = SD \cap \left( {ABM} \right)$.

Chỉ có $3$ vị trí tương đối của đường thẳng và mặt phẳng:

Nếu đường thẳng song song với mặt phẳng thì số điểm chung là giữa chúng là $0$

Nếu đường thẳng cắt mặt phẳng tại $1$ điểm duy nhất thì số điểm chúng là $1$

Nếu đường thẳng nằm trong mặt phẳng thì giữa chúng có vô số điểm chung.

Khi $M$ là giao điểm của đường thẳng $a$ và mặt phẳng $\left( P \right)$ thì $M \in a$ và $M \in \left( P \right)$ và tồn tại đường thẳng $b \subset \left( P \right)$ đi qua $M$, do đó $M$ là giao điểm của $a$ và $b$

Nếu đường thẳng $a$ cắt mặt phẳng $\left( P \right)$ tại $M$ thì $M \in \left( P \right)$.

Hơn nữa, các mặt phẳng chứa $a$ thì cũng chứa $M$ nên chúng đều có điểm chung với $\left( P \right)$, do đó đều cắt $\left( P \right)$.

+ Ta có $\left( \beta  \right)$ là mặt phẳng chứa đường thẳng b

+ Giao tuyến của $\left( \beta  \right)$ và $\left( \alpha  \right)$  là $d$

+ Giao điểm của $d$ và $b$ là $M$

$\Rightarrow M$ là giao điểm của $b$ và $\left( \alpha  \right)$

Vậy $M$ nằm trên đường thẳng $d$

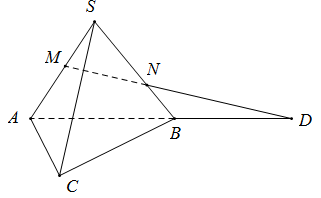
Ta có $MN \subset \left( {SAB} \right)$

$\left( {SAB} \right) \cap \left( {ABC} \right) = AB$

Gọi $D$  là giao điểm của $MN$  và $AB$

$\Rightarrow D$  là giao điểm của $MN$  và $\left( {ABC} \right)$

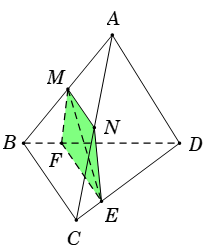
Tam giác $ABC$ có $M,\,\,N$ lần lượt là trung điểm của $AB,\,\,AC\,.$

Suy ra $MN$ là đường trung bình của tam giác $ABC$ $\Rightarrow \,\,MN$//$BC\,.$

Từ $E$ kẻ đường thẳng $d$ song song với $BC$ và cắt $BD$ tại $F\,\, \Rightarrow \,\,EF$//$BC.$

Do đó $MN//EF$ suy ra bốn điểm $M,\,\,N,\,\,E,\,\,F$ đồng phẳng và $MNEF$ là hình thang.

Vậy hình thang $MNEF$ là thiết diện cần tìm.

Vì $A \in d'$  mà $d' \subset \left( \alpha  \right)$  và $d' \subset \left( \beta  \right)$ nên $A \in \left( \alpha  \right)$  và $A \in \left( \beta  \right)$

Vì $A$  là giao điểm của $d$  và $d'$ nên $A \in d$

Mà $A \in \left( \alpha  \right)$  nên $A$  là giao điểm của $d$  và $\left( \alpha  \right)$

Khẳng định B là đúng