Cho bốn điểm $A,\,\,B,\,\,C,\,\,D$ không đồng phẳng. Gọi $M,\,\,N$ lần lượt là trung điểm của $AC$ và $BC.$ Trên đoạn $BD$ lấy điểm $P$ sao cho $BP = 2PD.$ Giao điểm của đường thẳng $CD$ và mặt phẳng $\left( {MNP} \right)$ là giao điểm của
Trả lời bởi giáo viên
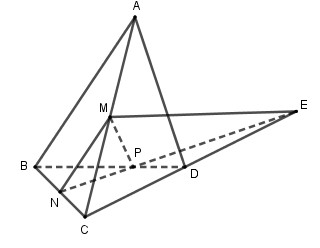
Cách 1. Xét mặt phẳng $\left( {BCD} \right)$ chứa $CD\,.$
Do $NP$ không song song $CD$ nên $NP$ cắt $CD$ tại $E\,.$
Điểm $E \in NP\,\, \Rightarrow \,\,E \in \left( {MNP} \right).$ Vậy $CD \cap \left( {MNP} \right)$ tại $E.$
Hướng dẫn giải:
Tìm một đường thẳng nằm trong mặt phẳng này mà cắt đường thẳng kia ta được giao điểm cần tìm.
Giải thích thêm:
Cách 2. Ta có $\left\{ \begin{array}{l}N \in BC\\P \in BD\end{array} \right. \Rightarrow NP \subset \left( {BCD} \right)$ suy ra $NP,\,\,CD$ đồng phẳng.
Gọi $E$ là giao điểm của $NP$ và $CD$ mà $NP \subset \left( {MNP} \right)$ suy ra $CD \cap \left( {MNP} \right) = E\,.$
Vậy giao điểm của $CD$ và $mp\;\left( {MNP} \right)$ là giao điểm $E$ của $NP$ và $CD\,.$

