Câu hỏi:
2 năm trước
Cho bốn điểm \(A,B,C,S\) không cùng ở trong một mặt phẳng. Gọi \(I,H\) lần lượt là trung điểm của \(SA,AB\). Trên \(SC\) lấy điểm \(K\) sao cho \(IK\) không song song với \(AC\) (\(K\) không trùng với các đầu mút). Gọi \(E\) là giao điểm của đường thẳng \(BC\) với mặt phẳng \(\left( {IHK} \right)\). Mệnh đề nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
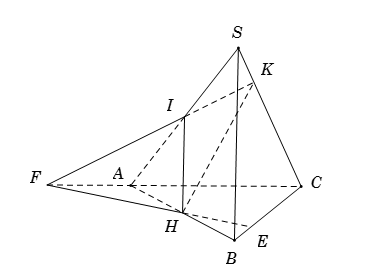
+) Chọn mặt phẳng phụ \(\left( {ABC} \right)\) chứa \(BC\).
+) Tìm giao tuyến của hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {IHK} \right)\).
Ta có \(H\) là điểm chung thứ nhất của \(\left( {ABC} \right)\) và \(\left( {IHK} \right)\).
Trong mặt phẳng \(\left( {SAC} \right)\), do \(IK\) không song song với \(AC\) nên gọi \(F = IK \cap AC\). Ta có
▪ \(F \in AC\) mà \(AC \subset \left( {ABC} \right)\) suy ra \(F \in \left( {ABC} \right)\).
▪ \(F \in IK\) mà \(IK \subset \left( {IHK} \right)\) suy ra \(F \in \left( {IHK} \right)\).
Suy ra \(F\) là điểm chung thứ hai của \(\left( {ABC} \right)\) và \(\left( {IHK} \right)\).
Do đó \(\left( {ABC} \right) \cap \left( {IHK} \right) = HF\).
+) Trong mặt phẳng \(\left( {ABC} \right)\), gọi \(E = HF \cap BC\). Ta có
▪ \(E \in HF\) mà \(HF \subset \left( {IHK} \right)\) suy ra \(E \in \left( {IHK} \right)\).
▪ \(E \in BC\).
Vậy \(E = BC \cap \left( {IHK} \right)\).
Hướng dẫn giải:
- Tìm giao tuyến của hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {IHK} \right)\).
- Tìm giao điểm của đường thẳng \(BC\) với giao tuyến vừa tìm.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
