Hai đường thẳng song song

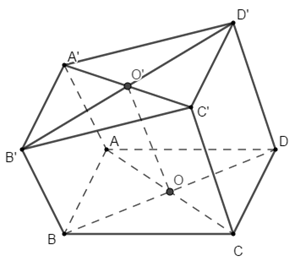
Do \(Ax,\,\,By,\,\,Cz,\,\,Dt\) song song với nhau cắt mặt phẳng \(\left( \alpha  \right)\) lần lượt tại \(A',\,\,B',\,\,C',\,\,D'\)  nên \(A'B'C'D'\) là hình bình hành và có tâm là \(O'\).

Gọi \(O\) là tâm hình bình hành \(ABCD\).

Ta có \(OO'\) là đường trung bình của hình thang \(BDD'B',\,\,ACC'A'\).

\(\begin{array}{l} \Rightarrow \dfrac{{A'A + CC'}}{2} = O'O = \dfrac{{BB' + D'D}}{2}\\ \Leftrightarrow A'A + CC' = BB' + D'D\\ \Leftrightarrow A'A = 5,2 + 7,8 - 8,6 = 4,4cm\end{array}\)

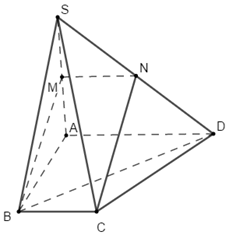
Từ \(M\) kẻ đường thẳng song song với \(BC\) cắt \(SD\) tại \(N\)\( \Rightarrow MN\parallel BC\) hay \( \Rightarrow MN\parallel BC\)

Mà \(M\) là trung điểm của \(SA\) nên \(N\) là trung điểm của SD.

Hai đường thẳng không có điểm chung thì chúng song song (khi chúng đồng phẳng) hoặc chéo nhau (khi chúng không đồng phẳng).

A sai. Trong trường hợp 2 đường thẳng cắt nhau thì chúng chỉ có 1 điểm chung.

B và C sai. Hai đường thẳng song song khi và chỉ khi chúng đồng phằng và không có điểm chung.

A sai. Hai đường thẳng chéo nhau thì chúng không có điểm chung.

C sai. Có thể xảy ra trường hợp hai đường thẳng đó hoặc cắt nhau hoặc trùng nhau.

D sai. Có thể xảy ra trường hợp hai đường thẳng đó song song.

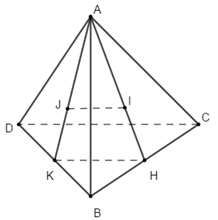
Bước 1:

Gọi \(H,\,\,K\) lần lượt là trung điểm của \(BC,\,\,BD\) \( \Rightarrow HK\parallel CD;HK = \dfrac{1}{2}CD\,\,\,\left( 1 \right)\).

Bước 2:

\(\Delta ABC\) có trọng tâm \(I\), trung tuyến \(AH \Rightarrow \dfrac{{AI}}{{AH}} = \dfrac{2}{3}\).

Tương tự ta có \(\dfrac{{AJ}}{{AK}} = \dfrac{2}{3}\)

Bước 3:

\( \Rightarrow \dfrac{{AI}}{{AH}} = \dfrac{{AJ}}{{AK}} \Rightarrow JI\parallel HK\) (Định lí ta-lét đảo)(2)

=> \(\dfrac{{IJ}}{{HK}} = \dfrac{{AI}}{{AK}} = \dfrac{2}{3} \Rightarrow JI = \dfrac{2}{3}HK\)(3)

Từ (1); (2) và (3) suy ra \(JI\parallel CD;\,\,JI = \dfrac{1}{3}CD\)

Hai đường thẳng được gọi là chéo nhau nếu chúng không đồng phẳng

Hai đường thẳng được gọi là song song nếu chúng đồng phẳng và không có điểm chung.

Hai đường thẳng có một điểm chung duy nhất thì chúng cắt nhau.

Hai đường thẳng song song với nhau thì chúng đồng phẳng và không có điểm chung.

Mặt phẳng được xác định nếu biết ba điểm không thẳng hàng nằm trong nó, hai đường thẳng cắt nhau nằm trong nó hoặc hai đường thẳng song song nằm trong nó.

Trường hợp ba điểm phân biệt thì chưa chắc đã xác định được mặt phẳng vì nếu ba điểm đó thẳng hàng thì ta không xác định được duy nhất mặt phẳng.

Tính chất của hai đường thẳng song song:

- Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.

- Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Từ hai tính chất trên ta thấy chỉ có đáp án A đúng.

B sai. Nếu 3 đường thẳng trùng nhau thì chúng sẽ cùng thuộc 1 mặt phẳng.

C sai. Nếu 3 đường thẳng trên chứa 3 cạnh của một tam giác khi đó sẽ tạo được 3 điểm phân biệt không thẳng hàng (là 3 đỉnh của tam giác), chúng lập thành 1 mặt phẳng xác định, 3 đường thẳng sẽ cùng thuộc 1 mặt phẳng

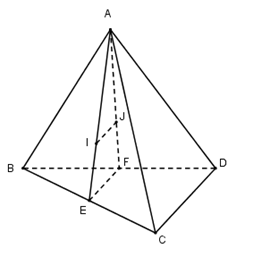
Gọi $E, F$ lần lượt là trung điểm của $BC$ và $BD$ ta có:

$\begin{array}{l}I \in AE\,;\,\dfrac{{AI}}{{AE}} = \dfrac{2}{3}\\J \in AF\,;\,\dfrac{{AJ}}{{AF}} = \dfrac{2}{3}\end{array}$

Xét trong $mp(AEF)$ ta suy ra \(IJ//EF\) (Định lí Ta – let đảo)

Mà $EF$ là đường trung bình của tam giác $ABC$ \( \Rightarrow \) $EF // CD$

Vậy $IJ // CD.$

Hai đường thẳng phân biệt nếu không có điểm chung (không cắt nhau) thì có thể song song hoặc chéo nhau nên A, B, C sai, D đúng.

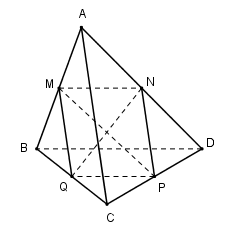
Ta có: $MN, PQ$ lần lượt là đường trung bình của tam giác $ABD$ và $CBD$ nên

$MN // BD ;$ \(MN = \dfrac{1}{2}BD\) và $ PQ // BD ;$ \(PQ = \dfrac{1}{2}BD\)

\( \Rightarrow \) $MN // PQ$ và $MN = PQ$

Do đó $MNPQ $ là hình bình hành nên $MP,NQ$ cùng thuộc một mặt phẳng.

Vậy A sai.

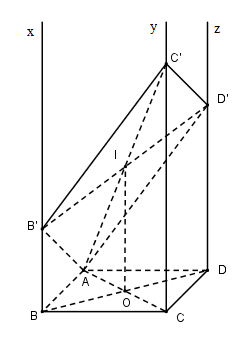
Trên $Bx$ và $Dz$ lấy điểm $B’$ và $D’$ sao cho $BB’ = 2, DD’ = 4.$

Gọi $O$ là tâm hình bình hành $ABCD, I $ là trung điểm của $B’D’$

Ta có $BDD’B’$ là hình thang, $OI$ là đường trung bình của hình thang nên $OI // BB’ // DD’ // Cy$ và \(OI = \dfrac{{BB' + {\rm{DD}}'}}{2} = \dfrac{{2 + 4}}{2} = 3\).

Xét mặt phẳng tạo bởi $OI$ và $CC’$ có: \(AI \cap Cy = C'\).

Ta có $OI // CC’, AO = OC$ suy ra $AI = IC’$

Suy ra $OI$ là đường trung bình của tam giác $ACC’$ \( \Rightarrow CC' = 2OI = 6\)

B sai vì hai đường thẳng phân biệt không cắt nhau thì có thể chéo nhau hoặc song song.

C sai vì hai đường thẳng phân biệt không song song thì có thể chéo nhau hoặc cắt nhau.

D sai vì hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau hoặc song song

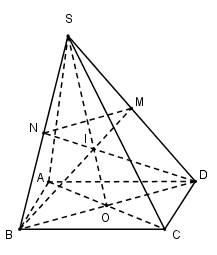
Dễ thấy $I$ là trọng tâm của tam giác $SBD $ nên $BI, DI$ là các đường trung tuyến của tam giác $SBD.$

Suy ra $M, N$ lần lượt là trung điểm của $SD$ và $SB.$

Nên $MN$ là đường trung bình của tam giác $SBD$ \( \Rightarrow \) $MN // BD.$

Vậy tứ giác $MNBD $ là hình thang.

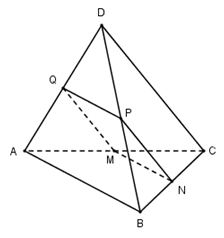
Vì $MN$ và $PQ$ lần lượt là đường trung bình của tam giác $ABC$ và $ABD$ nên:

\(\left\{ \begin{array}{l}MN//PQ//AB\\MN = PQ = \dfrac{1}{2}AB\end{array} \right. \Rightarrow \) MNPQ là hình bình hành.

Để $MNPQ $ trở thành hình thoi ta cần thêm yếu tố $MN = PN.$

Ta có: $PN$ là đường trung bình của tam giác $BCD$ nên \(PN = \dfrac{1}{2}CD\).

$MN = PN $ \( \Leftrightarrow \dfrac{1}{2}AB = \dfrac{1}{2}CD \Leftrightarrow AB = CD.\)

Vậy để $MNPQ $ là hình thoi cần thêm điều kiện $AB = CD.$