Phép vị tự

$\begin{array}{l}\left\{ \begin{array}{l}{V_{\left( {I; - 2} \right)}}\left( M \right) = M'\\{V_{\left( {I; - 2} \right)}}\left( N \right) = N'\end{array} \right. \Rightarrow M'N' = 2MN\\M\left( {3; - 4} \right);N\left( {0; - 2} \right) \Rightarrow MN = \sqrt {13} \\ \Rightarrow M'N' = 2\sqrt {13} \end{array}$

Đáp án A: Phép vị tự tâm là tâm đường tròn, tỉ số $k =  - 1$ vẫn biến đường tròn thành chính nó nên A sai.

Đáp án B: Phép vị tự tâm là trung điểm đoạn thẳng, tỉ số vị tự $k =  - 1$ biến đoạn thẳng thành chính nó nên B sai.

Đáp án C: Phép vị tự tâm $O$ tỉ số $k =  - 1$ biến một elip có tâm $O$ thành chính nó nên C đúng.

Đáp án D: Phép vị tự bất kì không biến một tia đi qua tâm vị tự thành chính nó nên D sai.

Theo tính chất phép vị tự, ta có $\overrightarrow {BD}  = 2\overrightarrow {AC}$.

Giả sử phép vị tự ${V_{\left( {O;k} \right)}}\,\,\left( {I;R} \right)\,\, \mapsto \,\,\left( {I';R} \right)$ ta có: $\left\{ \begin{array}{l}\overrightarrow {OI'}  = k\overrightarrow {OI} \\R' = \left| k \right|R\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {OI'}  = k\overrightarrow {OI} \\\left| k \right| = 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {OI'}  = \overrightarrow {OI}  \Rightarrow I \equiv I'\,\,\left( {ktm} \right)\\k = 1\end{array} \right.\\\left\{ \begin{array}{l}\overrightarrow {OI'}  =  - \overrightarrow {OI} \\k =  - 1\end{array} \right.\end{array} \right.$

Vậy có $1$  phép vị tự duy nhất biến $\left( {I;R} \right)$ thành $\left( {I';R} \right)$ là phép vị tự tâm $O$ với $O$ là trung điểm của $II'$  và tỉ số $k =  - 1$.

Ta có $R' = \left| k \right|.R = 5.R = 5.3 = 15.$

Gọi $M'\left( {x;y} \right)$. Suy ra $\overrightarrow {IM}  = \left( { - 9; - 1} \right),\,\,\overrightarrow {IM'}  = \left( {x - 2;y - 3} \right).$

Ta có ${V_{\left( {I, - 2} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  =  - 2\overrightarrow {IM}$ $\Rightarrow \left\{ \begin{array}{l}x - 2 =  - 2.\left( { - 9} \right)\\y - 3 =  - 2.\left( { - 1} \right)\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x = 20\\y = 5\end{array} \right. \Rightarrow M'\left( {20;5} \right)$

Ta có $\overrightarrow {AB}  = \left( { - 4;2} \right).$

Từ giả thiết, ta có $\overrightarrow {A'B'}  =  - \dfrac{1}{3}\overrightarrow {AB}  = \left( {\dfrac{4}{3}; - \dfrac{2}{3}} \right).$

Gọi $d'$  là ảnh của d qua ${V_{\left( {O;\dfrac{1}{2}} \right)}} \Rightarrow d'//d \Rightarrow$ phương trình $d'$  có dạng $3x - 2y + c = 0\,\,\left( {c \ne 4} \right)$

Lấy điểm $A\left( {0;2} \right) \in d$ , gọi ${V_{\left( {O;\dfrac{1}{2}} \right)}}\left( A \right) = A'\left( {x';y'} \right) \Rightarrow \overrightarrow {OA'}  = \dfrac{1}{2}\overrightarrow {OA}$

$\Rightarrow \left( {x';y'} \right) = \dfrac{1}{2}\left( {0;2} \right) \Leftrightarrow \left\{ \begin{array}{l}x' = 0\\y' = 1\end{array} \right. \Rightarrow A'\left( {0;1} \right)$

Mà ${V_{\left( {O;\dfrac{1}{2}} \right)}}\left( d \right) = d';{V_{\left( {O;\dfrac{1}{2}} \right)}}\left( A \right) = A' \Rightarrow A' \in d'$

Thay tọa độ điểm $A'$  vào phương trình đường thẳng $d'$  ta có: $3.0 - 2.1 + c = 0 \Leftrightarrow c = 2\,\,\left( {tm} \right)$

Vậy phương trình đường thẳng $d'$  là: $3x - 2y + 2 = 0$

Đường tròn $\left( C \right)$ có tâm $I\left( {1;3} \right)$ bán kính $R = 2$

Gọi $I'\left( {x';y'} \right)$ là ảnh của điểm $I$ qua phép vị tự ${V_{\left( {O;\dfrac{1}{2}} \right)}}$ ta có :

$\overrightarrow {OI'}  = \dfrac{1}{2}\overrightarrow {OI}  \Rightarrow \left( {x';y'} \right) = \dfrac{1}{2}\left( {1;3} \right) \Rightarrow \left\{ \begin{array}{l}x' = \dfrac{1}{2}\\y' = \dfrac{3}{2}\end{array} \right. \Rightarrow I'\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$

Gọi $\left( C \right)$  là ảnh của đường tròn $\left( C \right)$  qua phép vị tự ${V_{\left( {O;\dfrac{1}{2}} \right)}} \Rightarrow$ đường tròn $\left( {C'} \right)$ có tâm $I'\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$ và bán kính $R' = \left| {\dfrac{1}{2}} \right|R = 1$ , do đó $\left( {C'} \right)$ có phương trình ${\left( {x - \dfrac{1}{2}} \right)^2} + {\left( {y - \dfrac{3}{2}} \right)^2} = 1$.

Gọi $I\left( {x;y} \right)$.

Suy ra $\overrightarrow {IM}  = \left( {4 - x;6 - y} \right),\,\,\overrightarrow {IM'}  = \left( { - 3 - x;5 - y} \right).$

Ta có ${V_{\left( {I,\dfrac{1}{2}} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  = \dfrac{1}{2}\overrightarrow {IM}$$\Leftrightarrow \left\{ \begin{array}{l} - 3 - x = \dfrac{1}{2}\left( {4 - x} \right)\\5 - y = \dfrac{1}{2}\left( {6 - y} \right)\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x =  - 10\\y = 4\end{array} \right. \Rightarrow I\left( { - 10;4} \right)$

Từ giả thiết suy ra hình vuông ban đầu có độ dài cạnh bằng $2.$

Qua phép vị tự ${V_{\left( {I, - 2} \right)}}$ thì độ dài cạnh của hình vuông tạo thành bằng $4$, suy ra diện tích bằng $16.$

Vậy diện tích tăng gấp $4$ lần.

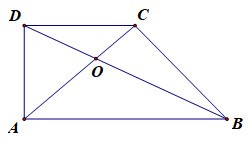
Gọi $O$ là giao điểm của $AC$ và $BD$

$\begin{array}{l}{V_{\left( {O;k} \right)}}\left( A \right) = C,\,\,\,{V_{\left( {O;k} \right)}}\left( B \right) = D\\ \Rightarrow \overrightarrow {CD}  = k\overrightarrow {AB}. \end{array}$

Mà $AB=3CD$ và $\overrightarrow {AB} ,\overrightarrow {CD}$ ngược hướng nên $k=-\dfrac{1}{3}$

$\begin{array}{l}d:x - 3y + 2 = 0\\d':x - 3y - 6 = 0\\V\left( {I;k} \right)d = d'\end{array}$

Lấy điểm $A\left( { - 2;0} \right) \in d$

$\begin{array}{l} \Rightarrow {V_{\left( {I;k} \right)}}\left( A \right) = A'\left( {x;y} \right) \in d'\\ \Leftrightarrow \overrightarrow {IA'}  = k\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 3 = k\left( { - 2-3} \right)\\y + 2 = k\left( {0 + 2} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 5k + 3\\y = 2k - 2\end{array} \right.\end{array}$

Thay tọa độ điểm $A'$ vào phương trình $d'$ ta có: $\left( { - 5k + 3} \right) - 3\left( {2k - 2} \right) - 6 = 0$$\Leftrightarrow k = \dfrac{3}{{11}}$

$\begin{array}{l}d:x - 2y + 6 = 0\\d':x - 2y - 6 = 0\\{V_{\left( {I;k} \right)}}\left( d \right) = d'\end{array}$

Lấy điểm $A\left( {0;3} \right) \in d$

$\begin{array}{l} \Rightarrow {V_{\left( {I;k} \right)}}\left( A \right) = A'\left( {x;y} \right) \in d'\\ \Leftrightarrow \overrightarrow {IA'}  = k\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 = k\left( {0 - 2} \right)\\y - 2 = k\left( {3 - 2} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 2k + 2\\y = k + 2\end{array} \right.\end{array}$

Thay tọa độ điểm $A'$ vào phương trình $d'$, ta có: $\left( { - 2k + 2} \right) - 2\left( {k + 2} \right) - 6 = 0$$\Leftrightarrow k =  - 2$

Bước 1:

Đường tròn $\left( C \right)$ có tâm $I\left( {8;4} \right)$ và bán kính $R = 2$

Bước 2:

Gọi $I'\left( {a';b'} \right)$ là ảnh của $I\left( {8;4} \right)$ qua ${V_{\left( {O;3} \right)}}$

$\left( {C'} \right)$ là ảnh của $\left( C \right)$ qua ${V_{\left( {O;3} \right)}}$, $R'$ là bán kính của $\left( {C'} \right)$

Bước 3:

Ta có $\left\{ \begin{array}{l}a' = 3.8 = 24\\b' = 3.4 = 12\end{array} \right. \Rightarrow I'\left( {24;12} \right)$.

Bước 4:

Phép vị tự không làm thay đổi bán kính của đường tròn nên $R' = k.R = 3.2 = 6$

Bước 5:

Ảnh của đường tròn $\left( C \right)$ qua phép vị tự tâm $O$ tỉ số $k = 3$ là đường tròn $\left( {C'} \right)$ có tâm $I'\left( {24;12} \right)$ và bán kính $R' = 6$.

Vậy phương trình đường tròn $\left( {C'} \right):{\left( {x - 24} \right)^2} + {\left( {y - 12} \right)^2} = 36$.

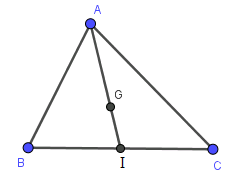
Bước 1:

Gọi $I$ là trung điểm của $BC$.

Bước 2:

Vì $G$ là trọng tâm tam giác $ABC$, ta có $IG = \dfrac{1}{3}IA$  suy ra $\overrightarrow {IG}  = \dfrac{1}{3}\overrightarrow {IA}$ 

Bước 3:

=> Có phép vị tự tâm $I$ tỉ số $\dfrac{1}{3}$ biến $A$ thành $G.$

Bước 4:

Gọi $O'$ là điểm sao cho $\overrightarrow {IO'}  = \dfrac{1}{3}\overrightarrow {IO}$

$\Rightarrow O'G = \dfrac{1}{3}.OA = \dfrac{R}{3}$(tính chất của phép vị tự)

Đường tròn $\left( {O;R} \right)$ cố định=> $\left( {O';\dfrac{R}{3}} \right)$ cố định

=> Điểm G luôn thuộc đường tròn $\left( {O';\dfrac{R}{3}} \right)$

Bước 5:

Mà phép vị tự tâm$I$ tỉ số $\dfrac{1}{3}$ biến đường tròn $\left( {O;R} \right)$ thành đường tròn $\left( {O';\dfrac{R}{3}} \right)$

Vậy quỹ tích điểm $G$ là ảnh của đường tròn $\left( {O;R} \right)$ qua phép vị tự tâm $I$ tỉ số $\dfrac{1}{3}$.

Bước 1:

Gọi $d' = {V_{\left( {O;2} \right)}}\left( d \right) \Rightarrow d'\parallel d \Rightarrow$ Phương trình $d'$ có dạng $3x - 2y + c = 0$.

Bước 2:

Lấy $A\left( { - 1; - 1} \right) \in d$. Gọi $A' = {V_{\left( {O;2} \right)}} \Rightarrow \overrightarrow {OA'}  = 2\overrightarrow {OA}  \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2.\left( { - 1} \right) =  - 2\\{y_{A'}} = 2.\left( { - 1} \right) =  - 2\end{array} \right. \Rightarrow A'\left( { - 2; - 2} \right)$.

Bước 3:

Vì $A' \in d' \Rightarrow 3.\left( { - 2} \right) - 2.\left( { - 2} \right) + c = 0 \Leftrightarrow c = 2$.

Vậy $d':\,\,3x - 2y + 2 = 0$.

Đáp án A, C hiển nhiên đúng.

Đáp án D đúng vì chỉ có phép vị tự tỉ số $k = 1$ biến 1 vector thành vector bằng nó, còn phép vị tự tỉ số $k \ne 1$ biến một vector thành một vector cùng phương với nó.

Ta có ${V_{\left( {O, - 3} \right)}}\left( A \right) = C \Leftrightarrow \overrightarrow {OC}  =  - \,3\,\overrightarrow {OA}$ và ${V_{\left( {O, - 3} \right)}}\left( B \right) = D \Leftrightarrow \overrightarrow {OD}  =  - \,3\,\overrightarrow {OB} .$

Khi đó $\overrightarrow {OC}  - \overrightarrow {OD}  =  - \,3\left( {\overrightarrow {OA}  - \overrightarrow {OB} } \right)$ $\Leftrightarrow \overrightarrow {DC}  =  - \,3\overrightarrow {BA}  \Leftrightarrow \overrightarrow {DC}  = 3\,\overrightarrow {AB}$

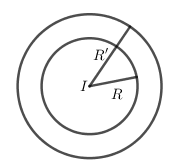
Hai đường tròn đồng tâm $I$, có $2$ phép vị tự tâm $I$ tỉ số $\pm \dfrac{{R'}}{R}$ biến đường tròn $\left( {I;R} \right)$ thành $\left( {I;R'} \right)$.