Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(B,C\) cố định, đỉnh \(A\) chạy trên một đường tròn \(\left( {O;R} \right)\) cố định không có điểm chung với đường thẳng \(BC\) và \(G\) là trọng tâm tam giác \(ABC.\) Khi đó quỹ tích trọng tâm \(G\) là ảnh của đường tròn \(\left( {O;R} \right)\) qua phép biến hình nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
Bước 1:
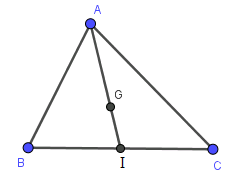
Gọi \(I\) là trung điểm của \(BC\).
Bước 2:
Vì \(G\) là trọng tâm tam giác \(ABC\), ta có \(IG = \dfrac{1}{3}IA\) suy ra \(\overrightarrow {IG} = \dfrac{1}{3}\overrightarrow {IA} \)
Bước 3:
=> Có phép vị tự tâm \(I\) tỉ số \(\dfrac{1}{3}\) biến \(A\) thành \(G.\)
Bước 4:
Gọi \(O'\) là điểm sao cho \(\overrightarrow {IO'} = \dfrac{1}{3}\overrightarrow {IO} \)
\( \Rightarrow O'G = \dfrac{1}{3}.OA = \dfrac{R}{3}\)(tính chất của phép vị tự)
Đường tròn \(\left( {O;R} \right)\) cố định=> \(\left( {O';\dfrac{R}{3}} \right)\) cố định
=> Điểm G luôn thuộc đường tròn \(\left( {O';\dfrac{R}{3}} \right)\)
Bước 5:
Mà phép vị tự tâm\(I\) tỉ số \(\dfrac{1}{3}\) biến đường tròn \(\left( {O;R} \right)\) thành đường tròn \(\left( {O';\dfrac{R}{3}} \right)\)
Vậy quỹ tích điểm \(G\) là ảnh của đường tròn \(\left( {O;R} \right)\) qua phép vị tự tâm \(I\) tỉ số \(\dfrac{1}{3}\).
Hướng dẫn giải:
Bước 1: Gọi \(I\) là trung điểm của \(BC\).
Bước 2: Biểu diễn \(\overrightarrow {IG} \) theo \(\overrightarrow {IA} \)
Bước 3: Tìm phép biến hình biến A thành G và xác định các yếu tố của phép biến hình đó.
Bước 4: Tìm quỹ tích của điểm \(G\).
Bước 5: Tìm phép biến hình và các yếu tố hình học của phép biến hình biến đường tròn \(\left( {O;R} \right)\) thành quỹ tích điểm G.
