Cho tam giác đều tâm $O.$ Với giá trị nào dưới đây của $\varphi $ thì phép quay ${Q_{\left( {O,\varphi } \right)}}$ biến tam giác đều thành chính nó?
Các góc quay để biến tam giác đều thành chính nó là \(0;\dfrac{{2\pi }}{3};\dfrac{{4\pi }}{3};2\pi .\)
Cho tam giác đều tâm $O.$ Hỏi có bao nhiêu phép quay tâm $O$ góc $\alpha $ với $0 \le \alpha < 2\pi $, biến tam giác trên thành chính nó?
Do $0 \le \alpha < 2\pi $ nên ta có các góc quay \(0;{\rm{ }}\dfrac{{2\pi }}{3};{\rm{ }}\dfrac{{4\pi }}{3}.\)
Cho phép quay \({Q_{\left( {O,\varphi } \right)}}\) biến điểm \(A\) thành điểm \(A'\) và biến điểm \(M\) thành điểm \(M'.\) Mệnh đề nào sau đây là sai?
Vì với góc quay khác \(k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\) thì hai vectơ \(\overrightarrow {AM} \) và \(\overrightarrow {A'M'} \) không cùng phương \( \Rightarrow \overrightarrow {AM} \ne \overrightarrow {A'M'} .\)
Trong mặt phẳng tọa độ $Oxy$ cho điểm $A\left( {3;0} \right)$. Tìm tọa độ điểm $A'$ là ảnh của điểm $A$ qua phép quay tâm $O\left( {0;0} \right)$ góc quay \(\dfrac{\pi }{2}.\)
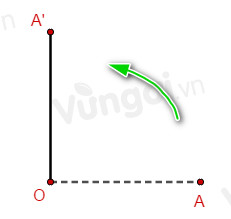
Gọi $A'\left( {x;y} \right).$ Ta có ${Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( A \right) = A' \Leftrightarrow \left\{ \begin{array}{l}OA = OA'\\\left( {\overrightarrow {OA} ,\overrightarrow {OA'} } \right) = \dfrac{\pi }{2}\end{array} \right..$
Vì $A\left( {3;0} \right) \in Ox \Rightarrow A'\left( {0;y} \right) \in Oy$ là ảnh của \(A\) qua phép quay tâm \(O\) góc quay \(\dfrac{\pi }{2}\).
Mà $OA = OA' \Rightarrow \left| y \right| = 3.$
Do góc quay $\varphi = \dfrac{\pi }{2} \Rightarrow y > 0$.
Vậy $A'\left( {0;3} \right)$.
Trong mặt phẳng tọa độ \(Oxy\) cho phép quay tâm \(O\) biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right).\) Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
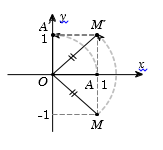
Từ giả thiết, kết hợp với hình vẽ ta thấy góc quay là \(\dfrac{\pi }{2}\).
Khi đó phép quay tâm \(O\) góc quay \(\dfrac{\pi }{2}\) biến điểm \(M\left( {1; - 1} \right)\) thành điểm \(M'\left( {1;1} \right).\)
Cho hình vuông tâm $O.$ Hỏi có bao nhiêu phép quay tâm $O$ góc $\alpha $ với $0 \le \alpha < 2\pi $, biến hình vuông trên thành chính nó?
Do $0 \le \alpha < 2\pi $ nên ta có các góc quay \(0;\dfrac{\pi }{2};\pi ;\dfrac{{3\pi }}{2}.\)
Cho hình chữ nhật tâm $O.$ Hỏi có bao nhiêu phép quay tâm $O$ góc $\alpha $ với $0 \le \alpha < 2\pi $, biến hình chữ nhật trên thành chính nó?
Do $0 \le \alpha < 2\pi $ nên ta có các góc quay \(0;\pi .\)
Trong mặt phẳng tọa độ \(Oxy\) cho hai đường thẳng \(a\) và \(b\) có phương trình lần lượt là \(4x + 3y + 5 = 0\) và \(x + 7y - 4 = 0.\) Nếu có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay \(\varphi \) \(\left( {0 \le \varphi \le {{180}^0}} \right)\) là:
Đường thẳng \(a:4x + 3y + 5 = 0\) có vectơ pháp tuyến \(\overrightarrow {{n_a}} = \left( {4;3} \right).\)
Đường thẳng \(b:x + 7y - 4 = 0\) có vectơ pháp tuyến \(\overrightarrow {{n_b}} = \left( {1;7} \right).\)
Góc \(\alpha \) là góc tạo bởi \(a\) và \(b\) ta có
\(\cos \alpha = \left| {\cos \left( {\overrightarrow {{n_a}} ,\overrightarrow {{n_b}} } \right)} \right| = \dfrac{{\left| {4.1 + 3.7} \right|}}{{\sqrt {{4^2} + {3^2}} \sqrt {{1^2} + {7^2}} }} = \dfrac{{\sqrt 2 }}{2} \Rightarrow \alpha = {45^0}.\)
Vậy \(\varphi = {45^0}.\)
Trong mặt phẳng tọa độ $Oxy$ cho hai điểm $M\left( {2;0} \right)$ và $N\left( {0;2} \right).$ Phép quay tâm $O$ biến điểm $M$ thành điểm $N$, khi đó góc quay của nó là:
Ta có $M$ thuộc tia $Ox$, \(N\) thuộc tia $Oy$$ \Rightarrow \varphi = 90^\circ .$
Cho tam giác \(ABC\) vuông tại \(B\) và góc tại \(A\) bằng \({60^0}\) (các đỉnh của tam giác ghi theo ngược chiều kim đồng hồ). Về phía ngoài tam giác vẽ tam giác đều \(ACD.\) Ảnh của cạnh \(BC\) qua phép quay tâm \(A\) góc quay \({60^0}\) là:
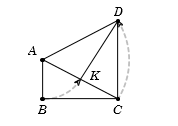
Từ giả thiết suy ra \(ABC\) là nữa tam giác đều, do đó \(AC = 2AB.\)
Xép phép quay tâm \(A\) góc quay \({60^0}\), ta có:
\( \bullet \) Biến \(B\) thành \(K;\)
\( \bullet \) Biến \(C\) thành \(D.\)
Vậy ảnh của \(BC\) là \(KD.\)
Cho hai đường thẳng bất kỳ \(d\) và \(d'\). Có bao nhiêu phép quay biến đường thẳng \(d\) thành đường thẳng \(d'\)?
Tâm quay là điểm cách đều hai đường thẳng.
Mệnh đề nào sau đây là sai?
Vì phép quay bảo toàn khoảng cách nên $OM' = OM.$
Cho hình thoi \(ABCD\) có góc \(\widehat {ABC} = {60^0}\) (các đỉnh của hình thoi ghi theo chiều kim đồng hồ). Ảnh của cạnh \(CD\) qua phép quay \({Q_{\left( {A,{{60}^0}} \right)}}\) là:
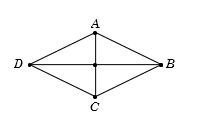
Xét phép quay tâm \(A\) góc quay \({60^0}:\)
\( \bullet \) Biến \(C\) thành \(B;\)
\( \bullet \) Biến \(D\) thành \(C.\)
Vậy ảnh của \(CD\) là \(BC.\)
Có bao nhiêu điểm biến thành chính nó qua phép quay tâm \(O\), góc quay \(\alpha = k2\pi \), \(k \in \mathbb{Z}\).
Phép quay tâm \(O\) góc quay \(\alpha = k2\pi \) biến một điểm bất kì thành chính nó.
Trên mặt phẳng có vô số điểm và vô số điểm đó đều biến thành chính nó qua phép quay trên.
Vậy có vô số điểm thỏa mãn bài toán.
Gọi \(I\) là tâm ngũ giác đều \(ABCDE\) (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây là sai?
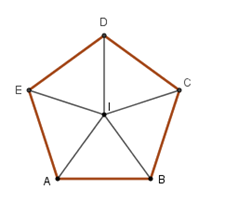
Bước 1:
Vì \(ABCDE\) là ngũ giác đều tâm \(I\) nên \(IA = IB = IC = ID = IE\) và \(\widehat {CID} = \widehat {DIE} = \widehat {EIA} = \widehat {AIB} = \widehat {BIC}\)\( = \dfrac{{360^\circ }}{5} = 72^\circ \)
Bước 2:
Từ đó ta có \({Q_{\left( {I;144^\circ } \right)}}\left( C \right) = E;{Q_{\left( {I;144^\circ } \right)}}\left( D \right) = A\)\( \Rightarrow {Q_{\left( {I;144^\circ } \right)}}\left( {CD} \right) = EA\) nên A đúng
\({Q_{\left( {I;72^\circ } \right)}}\left( A \right) = B;{Q_{\left( {I;72^\circ } \right)}}\left( B \right) = C\)\( \Rightarrow {Q_{\left( {I;72^\circ } \right)}}\left( {AB} \right) = BC\) nên B đúng.
\({Q_{\left( {I;72^\circ } \right)}}\left( A \right) = B;{Q_{\left( {I;72^\circ } \right)}}\left( E \right) = A\)\( \Rightarrow {Q_{\left( {I;72^\circ } \right)}}\left( {AE} \right) = BA\) nên C đúng.
\({Q_{\left( {I;144^\circ } \right)}}\left( B \right) = D;{Q_{\left( {I;144^\circ } \right)}}\left( C \right) = E\)\( \Rightarrow {Q_{\left( {I;144^\circ } \right)}}\left( {BC} \right) = DE\) nên D sai.
Trong hệ trục tọa độ \(Oxy\), cho đường thẳng \(d:3x - y + 1 = 0\). Tìm phương trình đường thẳng \(d'\) là ảnh của \(d\) qua phép quay \(Q\left( {O; - {{90}^0}} \right)\).
Bước 1:
Ta có \(\left( d \right):\,\,3x - y + 1 = 0\) có \(\overrightarrow {{n_d}} = \left( {3; - 1} \right)\).
Bước 2:
Lấy \(M\left( {0;1} \right) \in d\); Phép quay \({Q_{\left( {O; - 90^\circ } \right)}}\left( M \right) = M'\left( {a;b} \right)\)
Bước 3:
\( \Rightarrow \overrightarrow {OM} \left( {0;1} \right);\,\,\overrightarrow {OM'} \left( {a;b} \right)\)
Bước 4:
Phép quay \({Q_{\left( {O; - 90^\circ } \right)}}\left( d \right) = d'\) nên \(\left\{ \begin{array}{l}\overrightarrow {{n_d}} .\overrightarrow {{n_{d'}}} = 0\\OM' = OM = 1\\\overrightarrow {OM} .\overrightarrow {OM'} = 0\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{n_{d'}}} \left( {1;3} \right)\\{a^2} + {b^2} = 1\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_{d'}}} \left( {1;3} \right)\\b = 0\\a = 1(do\alpha = - 90^\circ )\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_{d'}}} \left( {1;3} \right)\\M'\left( {1;0} \right)\end{array} \right.\)
Bước 5:
Khi đó phương trình đường thẳng \(\left( {d'} \right)\) là \(x + 3y - 1 = 0.\)
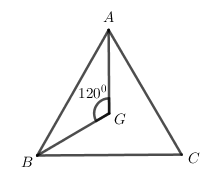
Cho tam giác $ABC$ đều với trọng tâm $G$. Phép quay tâm $G$ với góc nào dưới đây biến tam giác $ABC$ thành chính nó?
Ta thấy phép quay tâm $G$ góc \({120^0}\) biến điểm $A$ thành $B$ , biến điểm $B$ thành $C$ và biến điểm $C$ thành $A$, do đó phép quay tâm $G$ góc \({120^0}\) biến tam giác $ABC$ thành chính nó.
Cho phép quay \(Q\left( {O;\alpha } \right)\) biến điểm $A$ thành điểm $M$ và các khẳng định sau:
a) $O$ cách đều $A$ và $M$
b) $O$ thuộc đường tròn đường kính $AM$.
c) Góc lượng giác \((OA,OM) = \alpha \)
Số khẳng định đúng là:
Phép quay tâm $O$ góc \(\alpha \) biến điểm $A$ thành điểm $M$ khi và chỉ khi $OA=OM$ và góc lượng giác $(OA,OM)=\alpha $
Vậy khẳng định a) và c) đúng, khẳng định b) sai vì \(O\) là tâm đường tròn đi qua hai điểm $A,M$, chưa chắc $AM$ là đường kính của đường tròn ấy.
Trong mặt phẳng $Oxy$ cho điểm \(M\left( {1;1} \right)\). Hỏi trong bốn điểm được cho ở các phương án dưới đây, điểm nào là ảnh của $M$ qua phép quay tâm $O$ , góc \({45^0}\).
Gọi điểm \(M'\left( {x';y'} \right)\) là ảnh của điểm \(M\left( {1;1} \right)\) qua phép quay tâm $O$ góc \({45^0}\) nên ta có:
\(\left\{ \begin{array}{l}x' = \cos {45^0} - \sin {45^0} = 0\\y' = \sin {45^0} + \cos {45^0} = \sqrt 2 \end{array} \right. \Rightarrow M'\left( {0;\sqrt 2 } \right) \equiv B\)
Cho hình vuông tâm $O$. Hỏi có bao nhiêu phép quay tâm $O$, góc quay \(\alpha \,\,\left( {0 < \alpha \le 360^0} \right)\) biến hình vuông đã cho thành chính nó.
$\begin{array}{l}
{Q_{\left( {O;{{90}^0}} \right)}}\left( A \right) = D\\
{Q_{\left( {O;{{90}^0}} \right)}}\left( B \right) = A\\
{Q_{\left( {O;{{90}^0}} \right)}}\left( C \right) = B\\
{Q_{\left( {O;{{90}^0}} \right)}}\left( D \right) = C\\
\Rightarrow {Q_{\left( {O;{{90}^0}} \right)}}\left( {ABCD} \right) = ABCD\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( A \right) = C\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( B \right) = D\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( C \right) = A\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( D \right) = B\\
\Rightarrow {Q_{\left( {O;{{180}^0}} \right)}}\left( {ABCD} \right) = ABCD\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( A \right) = B\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( B \right) = C\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( C \right) = D\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( D \right) = A\\
\Rightarrow {Q_{\left( {O;{{270}^0}} \right)}}\left( {ABCD} \right) = ABCD\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( A \right) = A\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( B \right) = B\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( C \right) = C\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( D \right) = D\\
\Rightarrow {Q_{\left( {O;{{360}^0}} \right)}}\left( {ABCD} \right) = ABCD
\end{array}$
Vậy có 4 phép quay cần tìm.