Câu hỏi:
2 năm trước
Trong mặt phẳng tọa độ $Oxy$ cho điểm $A\left( {3;0} \right)$. Tìm tọa độ điểm $A'$ là ảnh của điểm $A$ qua phép quay tâm $O\left( {0;0} \right)$ góc quay \(\dfrac{\pi }{2}.\)
Trả lời bởi giáo viên
Đáp án đúng: b
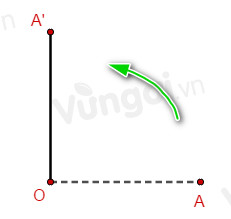
Gọi $A'\left( {x;y} \right).$ Ta có ${Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( A \right) = A' \Leftrightarrow \left\{ \begin{array}{l}OA = OA'\\\left( {\overrightarrow {OA} ,\overrightarrow {OA'} } \right) = \dfrac{\pi }{2}\end{array} \right..$
Vì $A\left( {3;0} \right) \in Ox \Rightarrow A'\left( {0;y} \right) \in Oy$ là ảnh của \(A\) qua phép quay tâm \(O\) góc quay \(\dfrac{\pi }{2}\).
Mà $OA = OA' \Rightarrow \left| y \right| = 3.$
Do góc quay $\varphi = \dfrac{\pi }{2} \Rightarrow y > 0$.
Vậy $A'\left( {0;3} \right)$.
Hướng dẫn giải:
- Nhận xét vị trí của \(A'\) trong mặt phẳng tọa độ.
- Tìm tọa độ của \(A'\) và kết luận.
