Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
Cho hai đường thẳng chéo nhau, có duy nhất một mặt phẳng qua đường thẳng này và song song với đường thẳng kia.
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
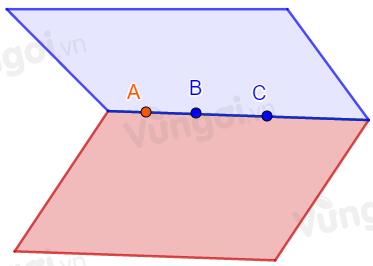
B sai. Trong trường hợp điểm thuộc đường thẳng đã cho, khi đó ra chỉ có 1 đường thẳng, có vô số mặt phẳng đi qua đường thẳng đó.
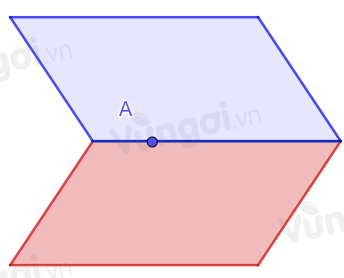
D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó
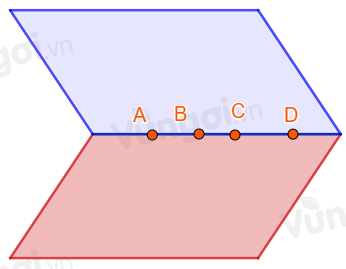
Hoặc trong trường hợp 4 điểm không đồng phẳng thì sẽ không tạo được mặt phẳng nào đi qua cả 4 điểm.
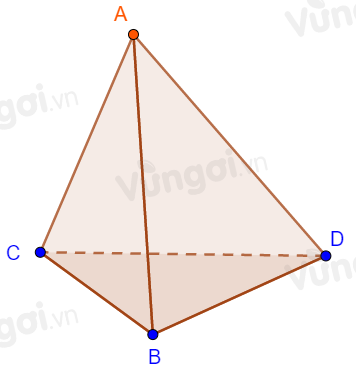
Tìm khẳng định đúng trong các khẳng định sau.
A. Đúng.
B. Sai vì hai mặt phẳng có thể trùng nhau.
C. Sai vì ba giao tuyến có thể song song hoặc trùng nhau.
D. Sai hai đường thẳng đó có thể trùng nhau hoặc chéo nhau hoặc cắt nhau.
Trong các mệnh đề sau, mệnh đề nào sai?
Mệnh đề “Hai đường thẳng không có điểm chung thì song song với nhau” chỉ đúng trong mặt phẳng, còn trong không gian thì hai đường thẳng không có điểm chung thì hoặc song song với nhau hoặc chéo nhau.
Hình chóp lục giác có bao nhiêu mặt bên?
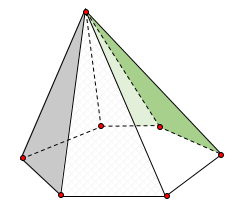
Quan sát hình vẽ ta thấy hình chóp lục giác đều có \(6\) mặt bên.
Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
Số mặt phẳng tạo thành là số cách chọn \(3\) trong \(4\) điểm đã cho.
Vậy có \(4\) mặt phẳng.
Tìm khẳng định sai trong các khẳng định sau đây ?
Xét đáp án D: Nếu mặt phẳng \(\left( P \right)\) có chứa hai đường thẳng phân biệt và hai đường thẳng đó cùng song song song với mặt phẳng \(\left( Q \right)\) thì mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\) là mệnh đề sai khi hai đường thẳng đó song song với nhau. Minh họa:
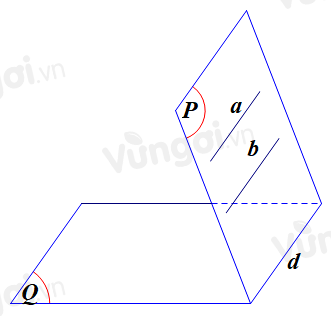
Từ hình trên ta thấy a song song b và a, b đều song song với (Q), và cùng nằm trong (P) nhưng (P) và (Q) không song song với nhau.
Lăng trụ tam giác có bao nhiêu mặt?
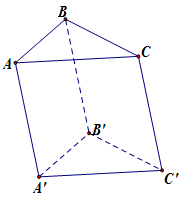
Lăng trụ tam giác có $5$ mặt gồm $3$ mặt bên và $2$ mặt đáy.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Giao tuyến của \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là
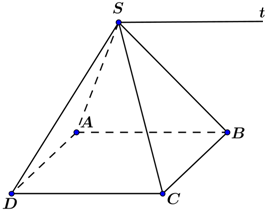
Xét ba mặt phẳng \(\left( {SAB} \right),\left( {SCD} \right),\left( {ABCD} \right)\) ta có:
\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SAB} \right) \cap \left( {SCD} \right) = d\end{array} \right.\)
Mà \(AB//CD\) nên \(AB//CD//d\)
Ngoài ra, \(S \in \left( {SAB} \right) \cap \left( {SCD} \right) = d\) nên giao tuyến \(d\) chính là đường thẳng đi qua \(S\) và song song với \(AB,CD\)
Cho tứ diện $ABCD$. Gọi $G$ và \(E\) lần lượt là trọng tâm của tam giác $ABD$ và $ABC$. Mệnh đề nào dưới đây đúng
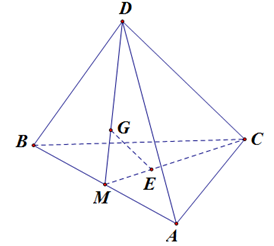
Gọi \(M\) là trung điểm của \(AB\). Trong tam giác \(MCD\) có \(\dfrac{{MG}}{{MD}} = \dfrac{{ME}}{{MC}} = \dfrac{1}{3}\) suy ra \(GE{\rm{//}}CD\)
Cho bốn mệnh đề sau:
(I) Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong mặt phẳng \( (\alpha )\) đều song song với $\left( \beta \right)$.
(II) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
(III) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
(IV) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước.
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
Có 3 mệnh đề sai là (II), (III), (IV).
(II) sai vì hai đường thẳng nằm trên hai mặt phẳng song song thì có thể song song hoặc chéo nhau.
(III) sai vì hai đường thẳng không có điểm chung thì có thể chéo nhau hoặc song song với nhau.
(IV) sai vì nếu tồn tại hai đường song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước thì cả bốn đường đó sẽ đồng phẳng (mâu thuẫn với dữ kiện hai đường thẳng ban đầu chéo nhau).
Cho tứ diện \(ABCD\). Gọi \(M\) là một điểm bất kì nằm trên đoạn \(AC\) (khác \(A\) và \(C\)). Mặt phẳng \(\left( P \right)\) qua \(M\) và song song với các đường thẳng \(AB\), \(CD\). Thiết diện của \(\left( P \right)\) với tứ diện đã cho là hình gì?
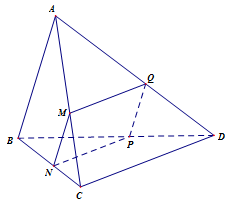
Trong mặt phẳng \(\left( {ABC} \right)\), kẻ \(MN\) song song \(AB\) và \(N\) thuộc cạnh \(BC\) \( \Rightarrow \left( P \right) \cap \left( {ABC} \right) = MN\).
Trong mặt phẳng \(\left( {BCD} \right)\), kẻ \(NP\) song song \(CD\) và \(P\) thuộc cạnh \(BD\) \( \Rightarrow \left( P \right) \cap \left( {BCD} \right) = NP\).
Trong mặt phẳng \(\left( {ABD} \right)\), kẻ \(PQ\) song song \(BA\) và \(Q\) thuộc cạnh \(AD\) \( \Rightarrow \left( P \right) \cap \left( {ABD} \right) = PQ\).
Và \(\left( P \right) \cap \left( {ACD} \right) = MQ\).
Do đó thiết diện của \(\left( P \right)\) với tứ diện đã cho là tứ giác \(MNPQ\)
Theo cách dựng thiết diện, ta có \(MN{\rm{ // }}QP\) và \(NP{\rm{ // }}MQ\) suy ra \(MNPQ\) là hình bình hành.
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật. Mặt phẳng \(\left( P \right)\) cắt các cạnh \(SA\), \(SB\), \(SC\), \(SD\) lần lượt tại $M$, \(N\), \(P\), \(Q\) . Gọi \(I\) là giao điểm của \(MQ\) và \(NP\). Câu nào sau đây đúng?
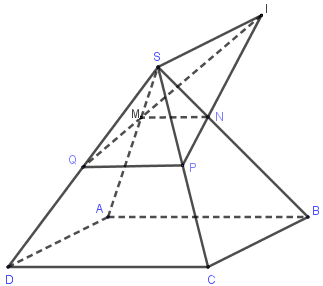
Xét ba mặt phẳng \(\left( {MNPQ} \right),\left( {SAD} \right),\left( {SCB} \right)\) ta có:
\(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SAD} \right) = MQ\\\left( {MNPQ} \right) \cap \left( {SBC} \right) = NP\\\left( {SAD} \right) \cap \left( {SBC} \right) = d\end{array} \right.\)
Mà \(MQ \cap NP = I\) nên \(d\) đi qua \(I\) hay giao tuyến của \(\left( {SAD} \right),\left( {SBC} \right)\) chính là \(SI\)
Ngoài ra, ta đã biết giao tuyến của \(\left( {SAD} \right),\left( {SBC} \right)\) là đường thẳng đi qua \(S\) và song song với \(AD,BC\)
Vậy \(SI//AD//BC\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), gọi \(I\) là trung điểm cạnh \(SC\). Mệnh đề nào sau đây sai ?
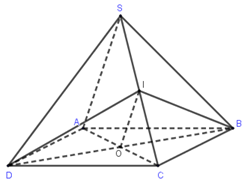
\(IO\) là đường trung bình tam giác \(SAC\) nên \(IO\,\,{\rm{//}}\,\,SA\)\( \Rightarrow IO\,{\rm{//}}\,\left( {SAB} \right)\), \(IO\,\,{\rm{//}}\,\,\left( {SAC} \right)\). Do đó A, B đúng.
\(I \in SC\), \(O = AC \cap BD\)\( \Rightarrow \left( {IBD} \right) \cap \left( {SAC} \right) = IO\) nên D đúng.
Cho hình chóp \(S.ABCD\) có đáy là hình thang đáy lớn là \(CD\). Gọi \(M\) là trung điểm của cạnh \(SA\), \(N\) là giao điểm của cạnh \(SB\) và mặt phẳng \(\left( {MCD} \right)\). Mệnh đề nào sau đây là mệnh đề đúng?

Xét ba mặt phẳng \(\left( {MCD} \right),\left( {SAB} \right),\left( {ABCD} \right)\) có:
\(\left\{ \begin{array}{l}\left( {MCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {MCD} \right) \cap \left( {SAB} \right) = MN\\\left( {ABCD} \right) \cap \left( {SAB} \right) = AB\end{array} \right.\)
Mà \(AB//CD\) nên \(MN//AB//CD\)
Vậy \(MN\;{\rm{//}}\;CD\).
Đáp án B đúng, D sai.
Ngoài ra, quan sát hình vẽ ta thấy \(MN,SD\) chéo nhau, \(MN,SC\) chéo nhau nên các đáp án A, C đều sai.
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trọng tâm của các tam giác \(ABC\), \(ABD\)
Những khẳng định nào sau là đúng?
\(\left( 1\right)\,:MN\;{\rm{//}}\;\left( {BCD} \right)\);
\(\left( 2\right)\,:MN\;{\rm{//}}\;\left( {ACD} \right)\);
\(\left( 3\right)\,:MN\;{\rm{//}}\;\left( {ABD} \right)\).
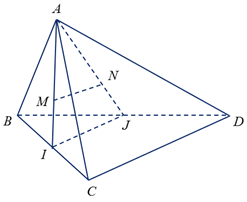
Gọi \(I\), \(J\) lần lượt là trung điểm \(BC\), \(BD\).
Ta có \(\dfrac{{AM}}{{AI}} = \dfrac{{AN}}{{{\rm{AJ}}}} = \dfrac{2}{3}\)\( \Rightarrow MN\;{\rm{//}}\;{\rm{IJ}}\) \( \Rightarrow MN\;{\rm{//}}\;IJ\;{\rm{//}}\;CD\) \( \Rightarrow \)\(MN\;{\rm{//}}\;\left( {BCD} \right)\) và \(MN\;{\rm{//}}\;\left( {ACD} \right)\).
Hai mặt phẳng song song có bao nhiêu mặt phẳng đối xứng?
Do mặt phẳng không có bề dày và không có giới hạn nên hai mặt phẳng song song có một mặt phẳng đối xứng là mặt phẳng nằm cách đều hai mặt phẳng song song đó và có vô số mặt phẳng đối xứng khác là các mặt phẳng vuông góc với hai mặt phẳng đã cho.
Cho hình lăng trụ $ABC.A'B'C'$. Gọi $I$, $J$, $K$ lần lượt là trọng tâm của các tam giác $ABC$, $ACC'$, $A'B'C'$. Mặt phẳng nào sau đây song song với mặt phẳng $\left( {IJK} \right)$?
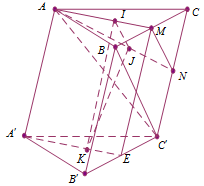
Gọi $M$, $N$, $E$ lần lượt là trung điểm của $BC$, $CC'$, $B'C'$. Suy ra $\dfrac{{AI}}{{IM}} = \dfrac{{AJ}}{{JN}} = 2$ (tính chất trọng tâm tam giác) nên $IJ{\rm{//}}MN$$\left( 1 \right)$.
Trong mặt phẳng $\left( {AA'EM} \right)$ ta có $\dfrac{{AI}}{{IM}} = \dfrac{{A'K}}{{KE}} = 2 \Rightarrow IK{\rm{//}}ME$ mà $ME{\rm{//}}BB'$ nên $IK{\rm{//}}BB'$$\left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ và do $\left( {IJK} \right)$ và $\left( {BB'C'} \right)$ là hai mặt phẳng phân biệt, $IJ,IK \subset \left( {IJK} \right)$ và $MN,BB' \subset \left( {BB'C'} \right)$
=>$\left( {IJK} \right){\rm{//}}\left( {BB'C'} \right)$.
Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(3a\), \(SA = SD = 3a\), \(SB = SC = 3a\sqrt 3 \). Gọi \(M\), \(N\) lần lượt là trung điểm của các cạnh \(SA\) và \(SD\), \(P\) là điểm thuộc cạnh \(AB\) sao cho \(AP = 2a\). Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( {MNP} \right)\).
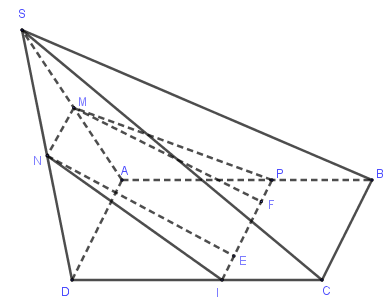
Do \(MN{\rm{//}}AD \Rightarrow MN{\rm{//}}BC\). Vậy \(\left( {MNP} \right)\) cắt mặt phẳng \(\left( {ABCD} \right)\) theo giao tuyến đi qua \(P\), song song \(BC\) và cắt \(DC\) tại điểm \(I\). Thiết diện của khối chóp cắt bởi mặt phẳng \(\left( {MNP} \right)\) chính là hình thang \(MNIP\).
Do \(\Delta NDI = \Delta MAP\) nên \(MP = NI\). Từ đó suy ra \(MNIP\) là hình thang cân.
Trong tam giác \(SAB\), ta có
\(\cos \widehat {SAB} = \dfrac{{S{A^2} + A{B^2} - S{B^2}}}{{2.SA.AB}} = \dfrac{{9{a^2} + 9{a^2} - 27{a^2}}}{{2.3a.3a}} = - \dfrac{{9{a^2}}}{{18{a^2}}} = - \dfrac{1}{2}\)
Trong tam giác\(MAP\), ta có \(M{P^2} = M{A^2} + A{P^2} - 2MA.AP.\cos \widehat {MAP} = \dfrac{{9{a^2}}}{4} + 4{a^2} + \dfrac{{3a}}{2} \cdot 2a = \dfrac{{37{a^2}}}{4} \Rightarrow MP = \dfrac{{a\sqrt {37} }}{2}\)
Từ \(M\) kẻ \(MF \bot PI\), từ \(N\) kẻ \(NE \bot PI\).
Dễ thấy, tứ giác \(MNEF\) là hình chữ nhật và từ đó suy ra \(MN = EF = \dfrac{{3a}}{2} \Rightarrow PF = EI = \dfrac{{3a}}{4}\)
Xét tam giác vuông \(MFP\), ta có \(MF = \sqrt {M{P^2} - F{P^2}} = \sqrt {\dfrac{{37{a^2}}}{4} - \dfrac{{9{a^2}}}{{16}}} = \dfrac{{a\sqrt {139} }}{4}\)
Ta có ${S_{MNIP}} = \dfrac{{\left( {MN + IP} \right).MF}}{2} = \dfrac{{\left( {\dfrac{{3a}}{2} + 3a} \right) \cdot \dfrac{{a\sqrt {139} }}{4}}}{2} = \dfrac{{9{a^2}\sqrt {139} }}{16}$
Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao ${\rm{150 m}}$, cạnh đáy dài ${\rm{220 m}}$. Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu?
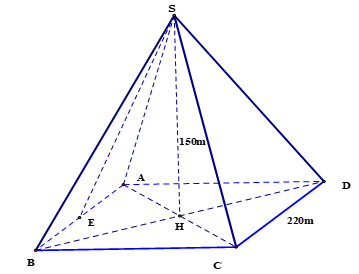
Dễ thấy $BD = \sqrt {B{C^2} + C{D^2}} = 220\sqrt 2 \,\, \Rightarrow BH = \dfrac{1}{2}BD = 110\sqrt 2 $
Trong tam giác vuông $SHB$, có $SB = \sqrt {S{H^2} + B{H^2}} = \sqrt {{{150}^2} + {{\left( {110\sqrt 2 } \right)}^2}} = 10\sqrt {467} $
Vì $S.ABCD$ là hình chóp đều $ \Rightarrow $$SA = SB = SC = SD = 10\sqrt {467} $
Gọi $E$ là trung điểm của $AB$
Trong tam giác vuông $SEA$, có $SE = \sqrt {S{A^2} - E{A^2}} = \sqrt {{{\left( {10\sqrt {467} } \right)}^2} - {{110}^2}} = 10\sqrt {346} $
Vậy ${S_{xq}} = 4{S_{ABC}} = 4.\dfrac{1}{2}SE.AB = 2.10\sqrt {346} .220 = 4400\sqrt {346} \,\left( {{{\rm{m}}^{\rm{2}}}} \right)$

