Cho tứ diện \(ABCD\). Gọi \(M\) là một điểm bất kì nằm trên đoạn \(AC\) (khác \(A\) và \(C\)). Mặt phẳng \(\left( P \right)\) qua \(M\) và song song với các đường thẳng \(AB\), \(CD\). Thiết diện của \(\left( P \right)\) với tứ diện đã cho là hình gì?
Trả lời bởi giáo viên
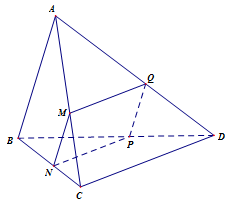
Trong mặt phẳng \(\left( {ABC} \right)\), kẻ \(MN\) song song \(AB\) và \(N\) thuộc cạnh \(BC\) \( \Rightarrow \left( P \right) \cap \left( {ABC} \right) = MN\).
Trong mặt phẳng \(\left( {BCD} \right)\), kẻ \(NP\) song song \(CD\) và \(P\) thuộc cạnh \(BD\) \( \Rightarrow \left( P \right) \cap \left( {BCD} \right) = NP\).
Trong mặt phẳng \(\left( {ABD} \right)\), kẻ \(PQ\) song song \(BA\) và \(Q\) thuộc cạnh \(AD\) \( \Rightarrow \left( P \right) \cap \left( {ABD} \right) = PQ\).
Và \(\left( P \right) \cap \left( {ACD} \right) = MQ\).
Do đó thiết diện của \(\left( P \right)\) với tứ diện đã cho là tứ giác \(MNPQ\)
Theo cách dựng thiết diện, ta có \(MN{\rm{ // }}QP\) và \(NP{\rm{ // }}MQ\) suy ra \(MNPQ\) là hình bình hành.
Hướng dẫn giải:
Xác định giao tuyến của mặt phẳng \(\left( P \right)\) với các mặt của tứ diện, sử dụng định lý giao tuyến ba mặt phẳng.

