Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là tứ giác có các cạnh đối diện không song song. Lấy điểm \(M\) thuộc miền trong tam giác \(SCD\). Tìm giao tuyến của hai mặt phẳng \(\left( {ABM} \right)\) và \(\left( {SCD} \right)\).
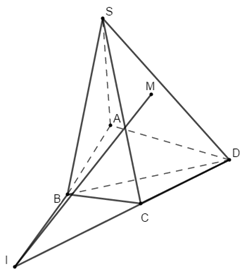
Bước 1:
Ta có \(M \in \left( {ABM} \right),M \in \left( {SCD} \right)\)\( \Rightarrow M \in \left( {ABM} \right) \cap \left( {SCD} \right)\).
Bước 2:
Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(I = AB \cap CD\).
\(I \in AB \Rightarrow I \in \left( {ABM} \right)\)\(;I \in CD \Rightarrow I \in \left( {SCD} \right)\)
\( \Rightarrow I \in \left( {ABM} \right) \cap \left( {SCD} \right)\)
Bước 3:
Vậy mặt phẳng \(\left( {AMB} \right),\,\,\left( {SCD} \right)\) có điểm chung là \(M\) và \(I\).
Nên \(MI\) là giao điểm của 2 mặt phẳng trên.
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng 6cm. Lấy điểm \(M\) trên cạnh \(SA\) sao cho \(SM = 2MA\). Diện tích thiết diện của tứ diện khi cắt bởi mặt phẳng qua \(M\) và song song với \(mp\left( {ABC} \right)\) là:
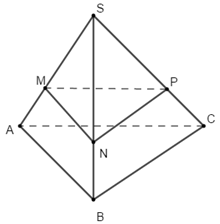
Bước 1:
Gọi \(N,\,P\) lần lượt thuộc \(SB,\,\,SC\) sao cho \(\dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{{SM}}{{SA}}\).
Bước 2:
=>\(NP||BC;MN||AB\).
Mà \(\left\{ \begin{array}{l}NP,MN \subset \left( {MNP} \right)\\AB,BC \subset \left( {ABC} \right)\\NP \cap MN = \left\{ N \right\}\\AB \cap BC = \left\{ B \right\}\end{array} \right.\)
\( \Rightarrow \left( {MNP} \right)||\left( {ABC} \right)\)
Bước 3:
Khi đó thiết diện của mặt phẳng qua \(M\) song song với \(\left( {ABC} \right)\) là tam giác \(MNP\).
Bước 4:
Áp dụng định lí ta-lét trong tam giác SAB có: \(\dfrac{{MN}}{{AB}} = \dfrac{{SM}}{{SA}} = \dfrac{2}{3} = 4\,\,\,\left( {SM = 2MA;SA = 6} \right)\)
Tương tự ta có \(NP = MP = 4cm.\)
Do đó tam giác \(MNP\) là tam giác đều cạnh 4cm.
Bước 5:
\( \Rightarrow {S_{MNP}} = \dfrac{{\sqrt 3 }}{4}{.4^2} = 4\sqrt 3 c{m^2}\)
Cho hai đường thẳng $a,b$ song song với nhau. Hai mặt phẳng $\left( P \right),\left( Q \right)$ phân biệt tương ứng chứa $a,b$ đồng thời cắt nhau theo giao tuyến $d$. Khi đó đường thẳng $d$:
Giao tuyến \(d\) của hai mặt phẳng có thể song song hoặc trùng với \(a\), nó cũng có thể song song hoặc trùng với \(b\). Trường hợp trùng xảy ra khi \(a = \left( P \right) \cap \left( Q \right)\) hoặc \(b = \left( P \right) \cap \left( Q \right)\)
Cho trước hai đường thẳng $a$ và $b$ chéo nhau. Khi đó:
Cho hai đường thẳng chéo nhau, khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với mặt phẳng kia.
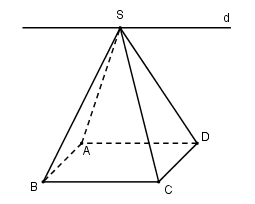
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $d$ là giao tuyến của hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SBC} \right)$ . Khẳng định nào sau đây là đúng?
Vì \(S \in \left( {SAD} \right)\) và \(S \in \left( {SBC} \right)\) nên \(S \in d\)
Ta có: \(\left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\BC \subset \left( {SBC} \right)\\AD//BC\\d = \left( {SAD} \right) \cap \left( {SBC} \right)\end{array} \right. \Rightarrow d//AD//BC\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang đáy lớn $AB$ . Gọi $M$ là một điểm trên cạnh \(CD;\left( \alpha \right)\) là mặt phẳng qua $M$ và song song với $SA$ và $BC$. Thiết diện của \(mp\left( \alpha \right)\) với hình chóp là:
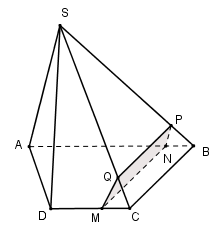
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ABCD} \right)\\BC\parallel \left( \alpha \right)\\BC \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {ABCD} \right) = MN\parallel BC\,\left( {N \in AB} \right)\,\,\left( 1 \right).\)
Tương tự $\begin{array}{l}\left\{ \begin{array}{l}N \in \left( \alpha \right) \cap \left( {SAB} \right)\\SA\parallel \left( \alpha \right)\\SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = NP\parallel SA\,\left( {P \in SB} \right)\\\left\{ \begin{array}{l}P \in \left( \alpha \right) \cap \left( {SBC} \right)\\BC\parallel \left( \alpha \right)\\BC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SBC} \right) = PQ\parallel BC\,\left( {Q \in SC} \right)\,\,\left( 2 \right).\end{array}$
Từ (1) và (2) suy ra $MN//PQ$ .
Vậy thiết diện là hình thang $MNPQ$ .
Cho tứ diện $ABCD$ có $AB = CD$ . Mặt phẳng \(\left( \alpha \right)\) qua trung điểm của $AC$ và song song với $AB,CD$ cắt $ABCD$ theo thiết diện là:
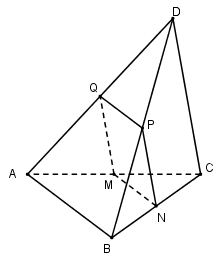
Gọi $M$ là trung điểm của $AC$ .
Trong $\left( {ABC} \right)$ qua $M$ kẻ \(MN//AB\left( {N \in BC} \right)\)
Trong $\left( {ACD} \right)$ và $\left( {BCD} \right)$ kẻ $MQ//CD$ và \(NP//CD\left( {Q \in AD,P \in BD} \right)\).
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ABC} \right)\\AB \subset \left( {ABC} \right)\\AB//\left( \alpha \right)\\MN//AB\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {ABC} \right) = MN.\)
Chứng minh tương tự ta có: \(\left( \alpha \right) \cap \left( {BCD} \right) = NP//CD\)
\(\begin{array}{l}\left( \alpha \right) \cap \left( {ABD} \right) = PQ//AB\\\left( \alpha \right) \cap \left( {ACD} \right) = QM//CD.\end{array}\)
Vậy thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) là tứ giác $MNPQ$ .
Ta có: $MN//PQ//AB,MQ//NP//CD$ nên $MNPQ$ là hình bình hành.
Ta có: $MN$ là đường trung bình của tam giác $ABC$ và $MQ$ là đường trung bình của tam giác $ACD$ nên \(MN = \dfrac{1}{2}AB,MQ = \dfrac{1}{2}CD.\)
Mà $AB = CD$ nên $MN = MQ$ . Vậy $MNPQ$ là hình thoi.
Cho hình lập phương $ABCD.A'B'C'D',AC$ và $BD$ cắt nhau tại $O,A'C'$ và $B'D'$ cắt nhau tại $O'$ . Các điểm $M,N,P$ theo thứ tự là trung điểm của $AB,BC,O'B'$. Khi đó thiết diện do mặt phẳng $\left( {MNP} \right)$ cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?
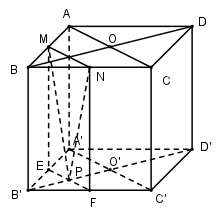
Ta có: $MN$ là đường trung bình của tam giác $ABC$ nên $MN//AC//A'C'$ .
$\left( {MNP} \right)$ và $\left( {A'B'C'D'} \right)$ có điểm $P$ chung và $MN//A'C'$ .
Qua $P$ kẻ \(EF//A'C';E \in A'B',F \in B'C'.\)
Vậy thiết diện của hình lập phương cắt bởi $mp\left( {MNP} \right)$ là $MNFE$.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang có cạnh đáy $AB$ và $CD$. Gọi $I,J$ lần lượt là trung điểm của các cạnh $AD$ và $BC$ và $G$ là trọng tâm tam giác $SAB$. Tìm giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {IJG} \right)$
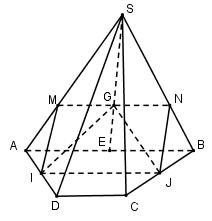
Ta có: $ABCD$ là hình thang và $I,J$ là trung điểm của $AD$ và $BC$ nên $IJ$ là đường trung bình của hình thang $ABCD$.
\( \Rightarrow IJ//AB//CD\) .
\(\left\{ \begin{array}{l}G \in \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right)\\AB \subset \left( {SAB} \right)\\{\rm{IJ}} \subset \left( {{\rm{IJ}}G} \right)\\AB//{\rm{IJ}}\end{array} \right. \Rightarrow \) Trong $\left( {SAB} \right)$ qua $G$ kẻ \(MN//AB\left( {M \in SA;N \in SB} \right)\)
\( \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN\) và $MN//IJ//AB//CD$ .
Cho chóp tứ giác $S.ABCD$ có hai đường chéo $AC$ và $BD$. Gọi $E$ và $F$ lần lượt là giao điểm của $AB$ và $CD,AD$ và $BC$ . Một mặt phẳng \(\left( \alpha \right)\) đi qua điểm $M$ trên cạnh $SB$ ($M$ nằm giữa $S$ và $B$ ) song song với $SE$ và $SF$ ($SE$ không vuông góc với $SF$). Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) có số cạnh là:
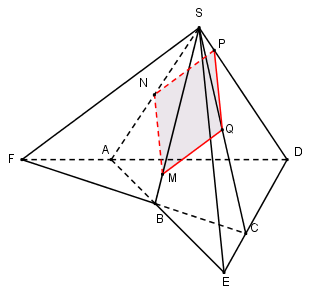
Giả sử thiết diện cần tìm đi qua điểm \(M \in SB.\)
Trong $\left( {SAB} \right)$ qua $M$ kẻ \(MN//SE\left( {N \in SA} \right)\) ta có:
\(\left( \alpha \right)\) và $\left( {SAB} \right)$ có điểm $M$ chung.
\(\begin{array}{l}\left( \alpha \right)//SE \subset \left( {SAB} \right)\\MN//SE\\ \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = MN.\end{array}\)
Tương tự trong $\left( {SAD} \right)$ qua $N$ kẻ \(NP//SF\left( {P \in SD} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SAD} \right) = NP.\)
Trong $\left( {SCD} \right)$ kẻ \(PQ//SE\left( {Q \in SC} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SCD} \right) = PQ.\)
\(\left( \alpha \right) \cap \left( {SBC} \right) = MQ.\)
Vậy thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác $MNPQ$.
Cho tứ diện $ABCD$. Trên cạnh $AD$ lấy trung điểm $M$, trên cạnh $BC$ lấy điểm $N$ bất kỳ. Gọi \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng $MN$ và song song với $CD$. Xác định vị trí của điểm $N$ trên cạnh $BC$ sao cho thiết diện là hình bình hành.
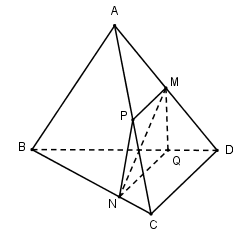
$\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ACD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ACD} \right)\end{array} \right.$
Suy ra $MP//CD$ với \(P \in CD\)
Tương tự \(\left\{ \begin{array}{l}N \in \left( \alpha \right) \cap \left( {BCD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {BCD} \right)\end{array} \right.\)
Suy ra \(NQ//CD\left( {Q \in BD} \right)\)
Vậy thiết diện là tứ giác $MPNQ$ có $MP//NQ//CD$ nên $MPNQ$ là hình thang.
Để $MPNQ$ là hình bình hành thì cần thêm điều kiện $MP = NQ$.
Mà \(MP = \dfrac{1}{2}CD\) (do $MP$ là đường trung bình của tam giác $ACD$).
Suy ra \(NQ = \dfrac{1}{2}CD\). Mà $NQ//CD$ nên $NQ$ là đường trung bình của tam giác $BCD$ .
Vậy $N$ là trung điểm của $BC$ hay \(NB = \dfrac{1}{2}BC\).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, tam giác $SBD$ cân tại $S$. Gọi $M$ là điểm tùy ý trên $AO$. Mặt phẳng \(\left( \alpha \right)\) đi qua $M$ và song song với $SA,BD$ cắt $SO,SB,AB$ tại $N,P,Q$. Tứ giác $MNPQ$ là hình gì?
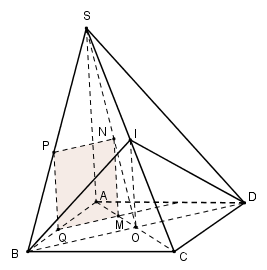
Tam giác $SBD$ cân tại $S$ nên $SB = SD$ .
Suy ra \(\Delta SBC = \Delta SDC\left( {c.c.c} \right) \Rightarrow \widehat {SCB} = \widehat {SCD}\).
Gọi $I$ là trung điểm của $SC$ .
Xét hai tam giác $IBC$ và $ICD$ có:
$IC$ chung
$BC = DC$ ($ABCD$ là hình vuông)
\(\widehat {ICB} = \widehat {ICD}\,\left( {cmt} \right)\)
Do đó \(\Delta IBC = \Delta IDC\left( {c.g.c} \right) \Rightarrow IB = ID\) hay tam giác $ICD$ cân tại $I$ .
Do $O$ là trung điểm của $BD$ nên $IO$ là đường trung tuyến trong tam giác cân \( \Rightarrow IO \bot BD.\)
Mà $SA//IO$ nên \(SA \bot BD.\)
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ABCD} \right)\\BD\parallel \left( \alpha \right)\\BD \subset \left( {ABCD} \right)\end{array} \right.\)
Suy ra giao tuyến của \(\left( \alpha \right)\) với $\left( {ABCD} \right)$ là đường thẳng qua $M$ và song song với $BD$ cắt $AB$ tại $Q$ \( \Rightarrow MQ\parallel BD.\,\,\left( 1 \right)\)
Ta có: \(\left\{ \begin{array}{l}Q \in \left( \alpha \right) \cap \left( {SAB} \right)\\SA\parallel \left( \alpha \right)\\SA \subset \left( {SAB} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\)với $\left( {SAB} \right)$ là đường thẳng đi qua $Q$ và song song với $SA$ cắt $SB$ tại $P$ . Do đó $QP//SA\left( 2 \right)$
Ta có: \(\left\{ \begin{array}{l}P \in \left( \alpha \right) \cap \left( {SBD} \right)\\BD\parallel \left( \alpha \right)\\BD \subset \left( {SBD} \right)\end{array} \right.\)suy ra giao tuyến của \(\left( \alpha \right)\)với $\left( {SBD} \right)$ là đường thẳng đi qua $P$ và song song với $BD$ cắt $SO$ tại $N$ . Do đó $PN//BD\left( 3 \right)$ .
Ta có: \(\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SAC} \right) = MN\\SA\parallel \left( \alpha \right)\\SA \subset \left( {SAC} \right)\end{array} \right. \Rightarrow MN\parallel SA.\) (4).
Từ (1) và (3) suy ra $PN//MQ//BD$ , từ (2) và (4) suy ra $QP//MN//SA$ . Do đó $MNPQ$ là hình bình hành.
Lại có \(SA \bot BD \Rightarrow MN \bot MQ\) .
Vậy $MNPQ$ là hình chữ nhật.
Cho hình chóp $S.ABCD$ . Gọi $M,N$ là hai điểm lần lượt thuộc cạnh $AB$ và \(CD;\left( \alpha \right)\) là mặt phẳng đi qua $MN$ và song song với $SA$ . Tìm điều kiện của $MN$ để thiết diện của hình chóp khi cắt bởi mp\(\left( \alpha \right)\) là một hình thang.
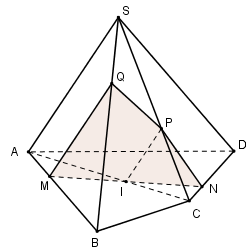
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right)\parallel SA\\SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = MQ\parallel SA\,\,\left( {Q \in SB} \right).\)
Trong (ABCD), gọi \(I = MN \cap AC\). Ta có:
\(\begin{array}{l}I \in MN,\,MN \subset \left( \alpha \right) \Rightarrow I \in \left( \alpha \right).\\I \in AC,\,AC \subset \left( {SAC} \right) \Rightarrow T \in \left( {SAC} \right)\\ \Rightarrow I \in \left( \alpha \right) \cap \left( {SAC} \right).\end{array}\)
Vậy \(\left\{ \begin{array}{l}I \in \left( \alpha \right) \cap \left( {SAC} \right)\\\left( \alpha \right)\parallel SA\\SA \subset \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {SAC} \right) \cap \left( \alpha \right) = IP\parallel SA\,\,\left( {P \in SC} \right).\)
Thiết diện là tứ giác $MNPQ$ .
Để tứ giác $MNPQ$ là hình thang thì cần $MQ//NP$ hoặc $MN//PQ$ .
Trường hợp 1: Nếu $MQ//NP$ thì
Ta có: \(\left\{ \begin{array}{l}MQ\parallel NP\\MQ\parallel SA\end{array} \right. \Rightarrow SA\parallel NP,\) mà \(NP \subset \left( {SCD} \right) \Rightarrow SA\parallel \left( {SCD} \right)\) (Vô lí).
Trường hợp 2: Nếu $MN//PQ$ thì ta có các mặt phẳng $\left( {ABCD} \right),\left( \alpha \right),\left( {SBC} \right)$ đôi một cắt nhau theo ba giao tuyến là $MN,BC,PQ$ nên $MN//BC$.
Đảo lại nếu $MN//BC$ thì \(\left\{ \begin{array}{l}PQ = \left( \alpha \right) \cap \left( {SBC} \right)\\MN \subset \left( \alpha \right)\\BC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow PQ\parallel MN\parallel BC\) nên tứ giác $MNPQ$ là hình thang.
Vậy tứ giác $MNPQ$ là hình thang thì điều kiện là $MN//BC$ .
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang có cạnh đáy $AB$ và $CD$ . Gọi I, J lần lượt là trung điểm của các cạnh $AD$ và $BC$ và $G$ là trọng tâm tam giác $SAB$. Tìm điều kiện của $AB$ và $CD$ để thiết diện của $\left( {IJG} \right)$ và hình chóp là một hình bình hành.
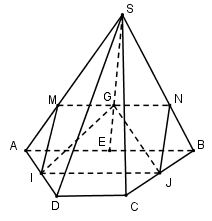
Ta có: $ABCD$ là hình thang và $I,J$ là trung điểm của $AD$ và $BC$ nên $IJ$ là đường trung bình của hình thang $ABCD$.
\( \Rightarrow IJ//AB//CD\) .
\(\left\{ \begin{array}{l}G \in \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right)\\AB \subset \left( {SAB} \right)\\{\rm{IJ}} \subset \left( {{\rm{IJ}}G} \right)\\AB//{\rm{IJ}}\end{array} \right. \Rightarrow \) Trong $\left( {SAB} \right)$ qua $G$ kẻ \(MN//AB\left( {M \in SA;N \in SB} \right)\)
\( \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN\) và $MN//IJ//AB//CD$ .
Dễ thấy thiết diện của $\left( {IJG} \right)$ và hình chóp là hình thang $MNJI$.
$G$ là trọng tâm của tam giác $SAB$ và $MN//AB$ nên theo định lí Ta-let ta có:
\(\dfrac{{MN}}{{AB}} = \dfrac{{SG}}{{SE}} = \dfrac{2}{3}\) (Với $E$ là trung điểm của $AB$).
\( \Rightarrow MN = \dfrac{2}{3}AB\)
Lại có: $IJ$ là đường trung bình của hình thang $ABCD$ nên ${\rm{IJ}} = \dfrac{{AB + CD}}{2}.$
Để hình thang $MNJI$ trở thành hình bình hành thì cần điều kiện $MN = IJ$.
\( \Rightarrow \dfrac{2}{3}AB = \dfrac{1}{2}\left( {AB + CD} \right) \Leftrightarrow \dfrac{1}{6}AB = \dfrac{1}{2}CD \Leftrightarrow AB = 3CD.\)
Cho hình chóp $S.ABCD,O$ là điểm nằm bên trong tam giác $ACD$. Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) đi qua $O$ và song song với $AC$ và $SD$ có số cạnh bằng:
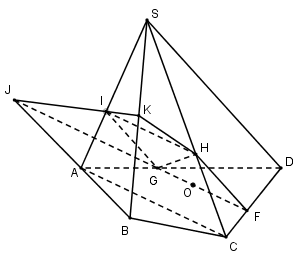
Trong $\left( {ABCD} \right)$ qua $O$ kẻ \(GF//AC\left( {G \in AD,F \in CD} \right)\)
Trong $\left( {SCD} \right)$ qua $F$ kẻ \(FH//SD\left( {H \in SC} \right)\)
\( \Rightarrow \left( \alpha \right)\) là $\left( {GFH} \right)$ .
\(\left( \alpha \right) \cap \left( {ABCD} \right) = GF,\left( \alpha \right) \cap \left( {SCD} \right) = HF.\)
Ta có: \(\left( \alpha \right)\) và $\left( {SAC} \right)$ có $H$ chung, \(\left( \alpha \right) \supset GF,\left( {SAC} \right) \supset AC,GF//AC\).
\( \Rightarrow \) Qua $H$ kẻ \(HI//AC\left( {I \in SA} \right)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {SAC} \right) = HI,\left( \alpha \right) \cap \left( {SAD} \right) = GI\).
Trong $\left( {ABCD} \right)$ gọi \(J = GF \cap AB \Rightarrow J \in AB \Rightarrow J \in \left( {SAB} \right)\)
Trong $\left( {SAB} \right)$ gọi \(K = IJ \cap SB\left( {K \in SB} \right)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = IK,\left( \alpha \right) \cap \left( {SBC} \right) = HK\)
Vậy thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) là $GFHKI$ là đa giác có $5$ cạnh.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$ là một điểm trên cạnh $SC$ và \(\left( \alpha \right)\) là mặt phẳng chứa $AM$ và song song với $BD$. Gọi $E$ và $F$ lần lượt là giao điểm của \(\left( \alpha \right)\) với các cạnh $SB,SD$ , gọi $I$ là giao điểm của $ME$ và $BC,J$ là giao điểm của $MF$ và $CD$. Nhận xét gì về ba điểm $I,J,A$?
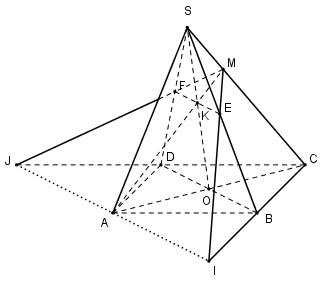
Giả sử dựng được điểm $E,F$ thỏa mãn yêu cầu bài toán.
Ta có: \(\left\{ \begin{array}{l}EF = \left( \alpha \right) \cap \left( {SBD} \right)\\\left( \alpha \right)\parallel BD\\BD \subset \left( {SBD} \right)\end{array} \right. \Rightarrow EF\parallel BD.\)
Do đó các điểm $E,F,A,M$ cùng thuộc mặt phẳng \(\left( \alpha \right)\).
Trong mặt phẳng \(\left( \alpha \right)\), gọi \(K = EF \cap AM.\)
Ta có: \(K \in EF,EF \subset \left( {SBD} \right) \Rightarrow K \in \left( {SBD} \right).\)
\(K \in AM,AM \subset \left( {SAC} \right) \Rightarrow K \in \left( {SAC} \right) \Rightarrow K \in \left( {SBD} \right) \cap \left( {SAC} \right).\)
Mà \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO\) với \(O = AC \cap BD \Rightarrow K \in SO.\)
Cách dựng $E,F$: Dựng giao điểm $K$ của $AM$ và $SO$ . Qua $K$ kẻ đường thẳng song song với $BD$ cắt $SB$ tại $E$ và cắt $SD$ tại $F$ .
Do \(\begin{array}{l}I = ME \cap BC\\I \in ME,ME \subset \left( \alpha \right) \Rightarrow I \in \left( \alpha \right)\\I \in BC,BC \subset \left( {ABCD} \right) \Rightarrow I \in \left( {ABCD} \right).\end{array}\)
Do đó \(I \in \left( \alpha \right) \cap \left( {ABCD} \right)\)
Tương tự ta cũng có \(J \in \left( \alpha \right) \cap \left( {ABCD} \right)\)và \(A \in \left( \alpha \right) \cap \left( {ABCD} \right)\)
Vậy $I,J,A$ cùng thuộc giao tuyến của \(mp\left( \alpha \right)\) và (ABCD).
Vậy $I,J,A$thẳng hàng.
Cho tứ diện đều $ABCD$ cạnh $a$ . Gọi $M$ và $P$ lần lượt là hai điểm di động trên các cạnh $AD$ và $BC$ sao cho $MA = PC = x\left( {0 < x < \dfrac{a}{2}} \right)$ . Mặt phẳng \(\left( \alpha \right)\) đi qua $MP$ song song với $CD$ cắt tứ diện theo một thiết diện là hình gì?
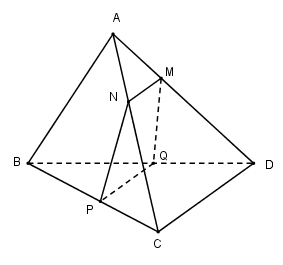
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ACD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ACD} \right)\end{array} \right.\)
Suy ra \(\left( \alpha \right) \cap \left( {ACD} \right) = MN\parallel CD\) với \(N \in AC\).
Tương tự \(\left( \alpha \right) \cap \left( {BCD} \right) = PQ\parallel CD\) với \(Q \in BD.\)
Vì $MN//CD//PQ$ nên thiết diện $MNPQ$ là hình thang.
Ta có $DQ = CP = x,DM = a-x$.
Áp dụng định lí Cosin trong tam giác $DMQ$ ta có:
\(MQ = \sqrt {D{M^2} + D{Q^2} - 2DM.DQ.cos60} = \sqrt {3{x^2} - 3ax + {a^2}} .\)
Tương tự ta cũng tính được \(NP = \sqrt {3{x^2} - 3ax + {a^2}} .\)
Suy ra $MQ = NP$ .
Mặt khác ta có
\(\begin{array}{l}MN = x < \dfrac{a}{2};PQ = a - x > \dfrac{a}{2}\\ \Rightarrow MN \ne PQ\end{array}\)
\( \Rightarrow MNPQ\) không là hình bình hành
Vậy thiết diện $MNPQ$ là hình thang cân.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a,SA = SB = SC = 2a.{\rm{ }}M$ là một điểm trên đoạn $SB$ mà $SM = m\left( {0 < m < 2a} \right)$. Mặt phẳng \(\left( \alpha \right)\) qua $M$ , song song với $SA,BC$ cắt hình chóp theo thiết diện có chu vi là:
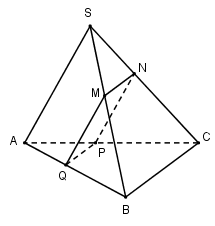
\(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right)//SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \) Qua $M$ kẻ \(MQ//SA\left( {Q \in AB} \right) \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = MQ.\)
Tương tự như trên ta xác định được
\(\begin{array}{l}\left( \alpha \right) \cap \left( {ABC} \right) = QP//BC\,\,\left( {P \in AC} \right)\\\left( \alpha \right) \cap \left( {SBC} \right) = MN//BC\,\,\left( {N \in BC} \right)\\\left( \alpha \right) \cap \left( {SAC} \right) = PN//SA\end{array}\)
Suy ra thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha \right)\) là hình bình hành $MNPQ.$
Áp dụng định lý Ta-let ta có:
\(\begin{array}{l}\dfrac{{MN}}{{BC}} = \dfrac{{SM}}{{SB}} \Rightarrow \dfrac{{MN}}{a} = \dfrac{m}{{2a}} \Rightarrow MN = \dfrac{m}{2}\\\dfrac{{QM}}{{SA}} = \dfrac{{BM}}{{BS}} \Rightarrow \dfrac{{QM}}{{2a}} = \dfrac{{2a - m}}{{2a}} \Rightarrow QM = 2a - m.\end{array}\)
Vậy chu vi hình bình hành $MNPQ$ là: \(2\left( {MN + QM} \right) = 2\left( {\dfrac{m}{2} + 2a - m} \right) = m + 4a - 2m = 4a - m.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang có đáy lớn $BC$ , đáy nhỏ $AD$. Mặt bên $\left( {SAD} \right)$ là tam giác đều, \(\left( \alpha \right)\) là mặt phẳng đi qua $M$ trên cạnh $AB$ , song song với $SA,BC$ . Mp\(\left( \alpha \right)\)cắt các cạnh $CD,SC,SB$ lần lượt tại $N,P,Q.MNPQ$ là hình gì?
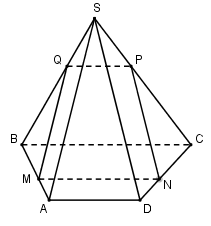
\(\begin{array}{l}\left\{ \begin{array}{l}BC//\left( \alpha \right),BC \subset \left( {ABCD} \right),BC \subset \left( {SBC} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( \alpha \right) \cap \left( {SBC} \right) = PQ\end{array} \right. \Rightarrow MN//BC//PQ\,\,\,\left( 1 \right).\\\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( \alpha \right)//SA,SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow SA//MQ.\end{array}\)
Áp dụng định lí Ta-let ta có: \(\dfrac{{AM}}{{AB}} = \dfrac{{SQ}}{{SB}} = \dfrac{{SP}}{{SC}};\dfrac{{AM}}{{AB}} = \dfrac{{DN}}{{DC}} \Rightarrow \dfrac{{SP}}{{SC}} = \dfrac{{DN}}{{DC}} \Rightarrow NP//SD.\)
\(\left\{ \begin{array}{l}MQ//SA\\MN//BC//AD\end{array} \right. \Rightarrow \widehat {NMQ} = \widehat {SAD} = {60^0}.\) (vì tam giác $SAD$ đều)
Tương tự ta chứng ming được \(\widehat {MNP} = \widehat {SDA} = {60^0} \Rightarrow \widehat {NMQ} = \widehat {MNP}\,\,\left( 2 \right).\)
Từ (1) và (2) suy ra $MNPQ$ là hình thang cân.
Cho tứ diện $ABCD$ có \(AB = a,CD = b,AB \bot CD\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$ . Mặt phẳng \(\left( \alpha \right)\) qua $M$ nằm trên đoạn $IJ$ và song song với $AB$ và $CD$. Giao tuyến của mặt phẳng \(\left( \alpha \right)\) và hình chóp có diện tích bằng bao nhiêu, biết $IJ = 3IM$
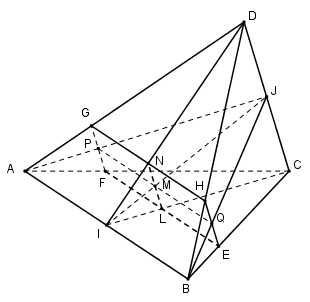
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ICD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ICD} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) và $\left( {ICD} \right)$ là đường thẳng qua $M$ và song song với $CD$ cắt $IC$ tại $L$ và cắt $ID$ tại $N$.
Tương tự \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {JAB} \right)\\AB\parallel \left( \alpha \right)\\AB \subset \left( {JAB} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) và $\left( {JAB} \right)$ là đường thẳng qua $M$ và song song $AB$ cắt $JA$ tại $P$ và cắt $JB$ tại $Q$.
Ta có: \(\left\{ \begin{array}{l}L \in \left( \alpha \right) \cap \left( {ABC} \right)\\AB\parallel \left( \alpha \right)\\AB \subset \left( {ABC} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) với $\left( {ABC} \right)$ là đường thẳng qua $L$ song song với $AB$ cắt $BC$ tại $E$ và cắt $AC$ tại $F$ . Do đó $EF//AB{\rm{ }}\left( 1 \right)$
Tương tự \(\left\{ \begin{array}{l}N \in \left( \alpha \right) \cap \left( {ABD} \right)\\AB\parallel \left( \alpha \right)\\AB \subset \left( {ABD} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\)và $\left( {ABD} \right)$ là đường thẳng qua $N$ song song với $AB$ cắt $BD$ tại $H$ và cắt $AD$ tại $G$ .
Do đó $HG//AB\left( 2 \right)$ .
Từ (1) và (2) suy ra EF // HG // AB (*)
Ta có: $\left\{ \begin{array}{l}FG = \left( \alpha \right) \cap \left( {ACD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {ACD} \right)\end{array} \right. \Rightarrow FG\parallel CD\,\,\,\left( 3 \right)$.
Tương tự \(\left\{ \begin{array}{l}EH = \left( \alpha \right) \cap \left( {BCD} \right)\\CD\parallel \left( \alpha \right)\\CD \subset \left( {BCD} \right)\end{array} \right. \Rightarrow EH\parallel CD\,\,\left( 4 \right).\)
Từ (*) và (**) suy ra $EFGH$ là hình bình hành.
Mà \(AB \bot CD \Rightarrow EF \bot FG.\) Vậy thiết diện $EFGH$ là hình chữ nhật
\( \Rightarrow {S_{EFGH}} = EF.FG = PQ.LN.\)
Trong tam giác $JAB$, ta có \(\dfrac{{PQ}}{{AB}} = \dfrac{{JM}}{{JI}} = \dfrac{2}{3} \Rightarrow PQ = \dfrac{{2AB}}{3} = \dfrac{{2a}}{3}.\)
Trong tam giác $ICD$ ta có \(\dfrac{{LN}}{{CD}} = \dfrac{{IM}}{{IJ}} = \dfrac{1}{3} \Rightarrow LN = \dfrac{{CD}}{3} = \dfrac{b}{3}.\)
Vậy diện tích thiết diện là: \({S_{EFGH}} = \dfrac{{2a}}{3}.\dfrac{b}{3} = \dfrac{{2ab}}{9}.\)

