Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng 6cm. Lấy điểm \(M\) trên cạnh \(SA\) sao cho \(SM = 2MA\). Diện tích thiết diện của tứ diện khi cắt bởi mặt phẳng qua \(M\) và song song với \(mp\left( {ABC} \right)\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
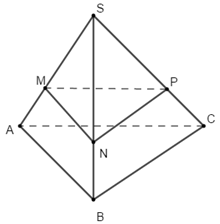
Bước 1:
Gọi \(N,\,P\) lần lượt thuộc \(SB,\,\,SC\) sao cho \(\dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{{SM}}{{SA}}\).
Bước 2:
=>\(NP||BC;MN||AB\).
Mà \(\left\{ \begin{array}{l}NP,MN \subset \left( {MNP} \right)\\AB,BC \subset \left( {ABC} \right)\\NP \cap MN = \left\{ N \right\}\\AB \cap BC = \left\{ B \right\}\end{array} \right.\)
\( \Rightarrow \left( {MNP} \right)||\left( {ABC} \right)\)
Bước 3:
Khi đó thiết diện của mặt phẳng qua \(M\) song song với \(\left( {ABC} \right)\) là tam giác \(MNP\).
Bước 4:
Áp dụng định lí ta-lét trong tam giác SAB có: \(\dfrac{{MN}}{{AB}} = \dfrac{{SM}}{{SA}} = \dfrac{2}{3} = 4\,\,\,\left( {SM = 2MA;SA = 6} \right)\)
Tương tự ta có \(NP = MP = 4cm.\)
Do đó tam giác \(MNP\) là tam giác đều cạnh 4cm.
Bước 5:
\( \Rightarrow {S_{MNP}} = \dfrac{{\sqrt 3 }}{4}{.4^2} = 4\sqrt 3 c{m^2}\)
Hướng dẫn giải:
Bước 1: Gọi \(N,\,P\) lần lượt thuộc \(SB,\,\,SC\) sao cho \(\dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{{SM}}{{SA}}\).
Bước 2: Chứng minh \(\left( {MNP} \right)\) là mặt phẳng qua M và song song với \(\left( {ABC} \right)\).
Bước 3: Tìm thiết diện của tứ diện bị cắt bởi \(\left( {MNP} \right)\).
Bước 4: Tính các cạnh của tam giác MNP.
Sử dụng định lý Ta-lét tính \(MN,NP.PM\)
Bước 5: Sử dụng công thức tính diện tích của tam giác đều cạnh a :
\(S = \dfrac{{\sqrt 3 }}{4}.{a^2}\)
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
