Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là tứ giác có các cạnh đối diện không song song. Lấy điểm \(M\) thuộc miền trong tam giác \(SCD\). Tìm giao tuyến của hai mặt phẳng \(\left( {ABM} \right)\) và \(\left( {SCD} \right)\).
Trả lời bởi giáo viên
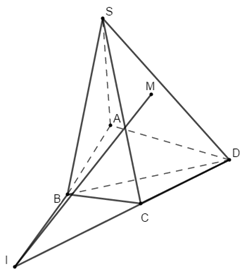
Bước 1:
Ta có \(M \in \left( {ABM} \right),M \in \left( {SCD} \right)\)\( \Rightarrow M \in \left( {ABM} \right) \cap \left( {SCD} \right)\).
Bước 2:
Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(I = AB \cap CD\).
\(I \in AB \Rightarrow I \in \left( {ABM} \right)\)\(;I \in CD \Rightarrow I \in \left( {SCD} \right)\)
\( \Rightarrow I \in \left( {ABM} \right) \cap \left( {SCD} \right)\)
Bước 3:
Vậy mặt phẳng \(\left( {AMB} \right),\,\,\left( {SCD} \right)\) có điểm chung là \(M\) và \(I\).
Nên \(MI\) là giao điểm của 2 mặt phẳng trên.
Hướng dẫn giải:
Bước 1: Tìm điểm chung (nếu có) của hai mặt phẳng trong các điểm bài đã cho.
Bước 2: Tìm giao điểm thứ 2 của hai mặt phẳng.
Tìm mặt phẳng chứa 2 đường thẳng lần lượt trên \(\left( {ABM} \right)\) và \(\left( {SCD} \right)\), lấy giao điểm của 2 đường thẳng đó.
Bước 3: Xác định giao tuyến.
Đường thẳng nối 2 điểm ở bước 1 và bước 2 là giao tuyến của \(\left( {ABM} \right)\) và \(\left( {SCD} \right)\).

