Đường thẳng song song với mặt phẳng

Đường thẳng và mặt phẳng nếu có hai điểm chung thì sẽ có vô số điểm chung nên không thể chỉ có hai điểm chung.

Nếu đường thẳng \(d\) và mặt phẳng \(\left( \alpha  \right)\) không có điểm chung thì chúng song song.

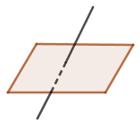
Từ hình vẽ ta thấy \(d\) cắt \(\left( \alpha  \right)\) tại duy nhất một điểm.

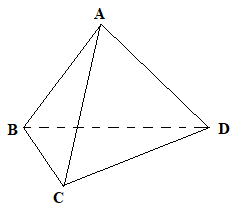
Từ hình vẽ ta thấy:

+) Đường thẳng \(AD\) cắt mặt phẳng \(\left( {ABC} \right)\) tại điểm duy nhất \(A\) nên đáp án A, B đều sai.

+) \(A \in \left( {ABC} \right),B \in \left( {ABC} \right) \Rightarrow AB \subset \left( {ABC} \right)\) nên C đúng.

+) Đường thẳng \(AC\) cắt mặt phẳng \(\left( {ABD} \right)\) tại điểm duy nhất \(A\) nên D sai.

Nếu đường thẳng \(d\) không nằm trong mặt phẳng \(\left( \alpha  \right)\) mà \(d\) song song với một đường thẳng \(d'\) nằm trong \(\left( \alpha  \right)\) thì \(d\) song song với \(\left( \alpha  \right)\).

Nếu đường thẳng \(d//\left( \alpha  \right)\) và \(d' \subset \left( \alpha  \right)\) thì \(d\) và \(d'\) có thể song song hoặc chéo nhau.

Vì \(d//\left( \alpha  \right)\) và \(d' \subset \left( \alpha  \right)\) nên \(d\) và \(d'\) chỉ có thể song song hoặc chéo nhau. Do đó chũng không có điểm chung.

Cho đường thẳng \(d\) song song với mặt phẳng \(\left( \alpha  \right)\), nếu mặt phẳng \(\left( \beta  \right)\) chứa \(d\) mà cắt \(\left( \alpha  \right)\) theo giao tuyến \(d'\) thì \(d//d'\).

Cho hai đường thẳng chéo nhau, có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

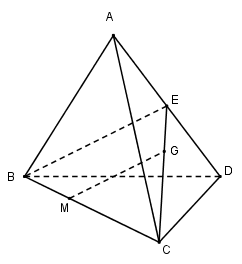
Gọi $E$ là trung điểm của $AD$ ta có \(G \in CE\) và \(\dfrac{{CG}}{{CE}} = \dfrac{2}{3}\)

Vì \(CM = 2MB \Rightarrow \dfrac{{CM}}{{CB}} = \dfrac{2}{3}\)

Xét tam giác $BCE$ có: \(\dfrac{{CG}}{{CE}} = \dfrac{{CM}}{{CB}} = \dfrac{2}{3} \)

\(\Rightarrow \) $MG // BE$ (Định lí Ta – let đảo)

Mà \(BE \subset \left( {ABD} \right)\) \( \Rightarrow \) $MG // (ABD)$

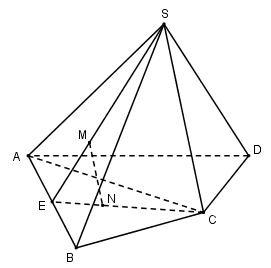
Gọi $E$ là trung điểm của $AB$ ta có:

\(\begin{array}{l}M \in SE\,;\,\dfrac{{EM}}{{ES}} = \dfrac{1}{3}\\N \in EC\,;\,\dfrac{{EN}}{{EC}} = \dfrac{1}{3}\end{array}\)

Xét tam giác $ESC$ ta có \(\dfrac{{EM}}{{ES}} = \dfrac{{EN}}{{EC}} = \dfrac{1}{3} \)

\(\Rightarrow \) $MN // SC$ (Định lí Ta – let đảo).

Mà \(SC \subset \left( {SCD} \right) \Rightarrow MN // (SCD)\)

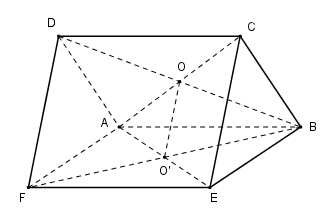
Vì $O$ và $O’$ lần lượt là tâm hình bình hành $ABCD $ và $ABEF$ nên $O$ là trung điểm của $BD;$ $O’$ là trung điểm của $FB.$

Xét tam giác $BDF $ có: $OO’$ là đường trung bình \( \Rightarrow \) $OO’ // DF$

Mà \(DF \subset \left( {DCEF} \right);\) \(DF \subset \left( {ADF} \right)\,;\) \(\,DF // \left( {BCE} \right)\)

Nên $OO’ // (DCEF) ;$ $ OO’ // (ADF) ;$ $ OO’ // (BCE)$ (cùng song song với DF).

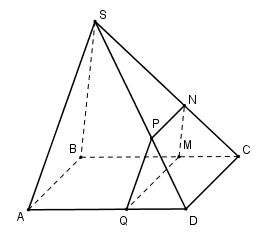
Vì $MN // BS $ nên \(\dfrac{{CN}}{{CS}} = \dfrac{{CM}}{{CB}}\) (Định lí Ta – let)  (1)

Vì $MQ // CD // AB$ nên \(\dfrac{{CM}}{{CB}} = \dfrac{{DQ}}{{DA}}\)                   (2)

Vì $NP // CD$ nên \(\dfrac{{CN}}{{CS}} = \dfrac{{DP}}{{DS}}\) (Định lí Ta – let)    (3)

Từ (1), (2) và (3) suy ra \(\dfrac{{DP}}{{DS}} = \dfrac{{DQ}}{{DA}}\) \( \Rightarrow PQ // SA\)  (Định lí Ta – let đảo)

Ta có: \(SA \subset \left( {SAB} \right)\,\,;\,\,SA \subset \left( {SAD} \right)\).

Tuy nhiên $PQ \subset \left( {SAD} \right)$ nên $PQ$ không song song với $mp(SAD).$

Ngoài ra $PQ$ không nằm trong $(SAB)$ nên $PQ//(SAB)$

Vậy $PQ // (SAB).$

A và D sai vì hai đường thẳng cùng song song với một mặt phẳng thì hai đường thẳng đó song song với nhau hoặc trùng nhau.

B sai vì hai đường thẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.

Các mệnh đề b, c, d đúng nên có $3$ mệnh đề đúng.

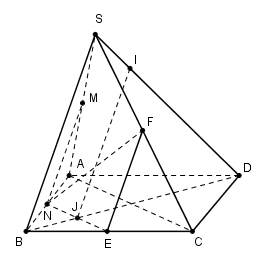
Trước hết ta lấy điểm \(M \in \left( P \right)\) sao cho \(M \in SA\).

Trong mp(SAB) kẻ MN // SA \(\left( {N \in AB} \right)\), trong mp(ABCD) kẻ NE // AC \(\left( {E \in BC} \right)\).

\(NE \cap BD = \left\{ J \right\}\)

Trong mp(SBC) kẻ EF // SB \(\left( {F \in SC} \right)\), trong mp(SBD) kẻ JI // SD \(\left( {I \in SD} \right)\).

Giả sử MN // (SCD)

Lại có: MN // SB\( \Rightarrow SB \subset \left( {SCD} \right)\) (vô lý) nên (1) sai.

Tương tự ta chứng minh được (2) sai.

NE // AC\( \subset \left( {SAC} \right) \Rightarrow \) NE // (SAC). Do đó (3) đúng.

IJ // SB\( \subset \left( {SAB} \right) \Rightarrow \)IJ // (SAB). Do đó (4) đúng.

Đường thẳng $a//(P)$ thì có vô số đường thẳng nằm trong $(P)$ và song song với $a$

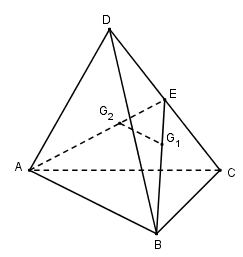
Gọi $E$ là trung điểm của $CD$\( \Rightarrow {G_1} \in BE;{G_2} \in AE \Rightarrow B{G_1};A{G_2};CD\) đồng quy tại $E.$ Suy ra C đúng.

Ta có: \(\dfrac{{E{G_1}}}{{EB}} = \dfrac{{E{G_2}}}{{EA}} = \dfrac{1}{3} \) \(\Rightarrow {G_1}{G_2}// AB\) và ${G_1}{G_2} = \dfrac{1}{3}AB$ (Định lí Ta-let đảo)

Mà \(AB \subset \left( {ABD} \right) \Rightarrow {G_1}{G_2}// (ABD)\) 

\(AB \subset \left( {ABC} \right) \Rightarrow {G_1}{G_2}// (ABC).\) 

Suy ra A và B đúng. Vậy D sai

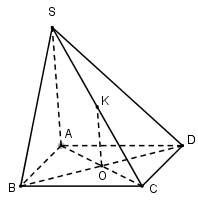
Gọi $O$ là giao điểm của $AC$ và $BD$

Trong mặt phẳng $SAC,$ qua $O$ kẻ ${\rm{O}}K \bot AC\,\,\left( {K \in SC} \right)$, suy ra $mp$\(\left( \alpha  \right)\) chính là $mp(BDK).$

$OK // SA ; AO = OC$\( \Rightarrow \) $SK = KC.$ (Định lí đường trung bình của tam giác)

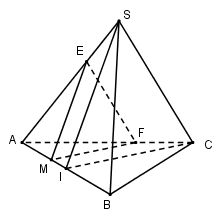
Trong $mp(ABC)$ kẻ $MF // IC$ \(\left( {F \in AC} \right)\), trong $mp(SAB)$ kẻ $ME // SI$ \(\left( {E \in SA} \right)\).

Do đó $mp(P)$ chính là $(MEF)$ và thiết diện tạo bởi $mp(P)$ và tứ diện đều $SABC$ là tam giác $MEF.$

Gọi $a$ là cạnh của tứ diện đều $SABC.$

Xét tam giác đều $ABC$ và tam giác $SAB$ là những tam giác đều cạnh $a$ nên \(CI = SI = \dfrac{{a\sqrt 3 }}{2}\).

Trong $(ABC)$ ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{ME}}{{SI}} \Leftrightarrow \dfrac{x}{{\dfrac{a}{2}}} = \dfrac{{ME}}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow ME = x\sqrt 3 .\)

Trong $(SAB)$ ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{MF}}{{CI}} \Leftrightarrow \dfrac{x}{{\dfrac{a}{2}}} = \dfrac{{MF}}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow MF = x\sqrt 3 .\)

Ta lại có: \(\dfrac{{AM}}{{AI}} = \dfrac{{AF}}{{AC}} = \dfrac{{AE}}{{AS}} \) \(\Rightarrow EF\) $// SC $ (Định lí Ta-let đảo)

\( \Rightarrow \dfrac{{EF}}{{SC}} = \dfrac{{AF}}{{AC}} = \dfrac{{AM}}{{AI}} \Leftrightarrow \dfrac{{EF}}{a} = \dfrac{x}{{\dfrac{a}{2}}} \Leftrightarrow EF = 2x\)

Vậy chu vi tam giác $MEF $ bằng $ME + MF + EF =$ \(x\sqrt 3  + x\sqrt 3  + 2x = 2x\left( {1 + \sqrt 3 } \right)\)