Cho tứ diện $ABCD,$ $M$ là trung điểm của cạnh $CD,$ $G$ là trọng tâm tứ diện. Khi đó 2 đường thẳng $AD$ và $GM $ là hai đường thẳng:
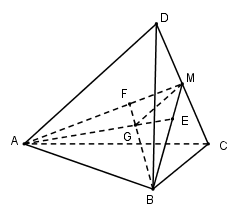
Gọi $M$ là trung điểm của $CD, E$ và $F$ lần lượt là trọng tâm tam giác $BCD$ và $ACD$ \( \Rightarrow E \in BM,F \in AM.\)
Trong $(AMB):$ \(G = AE \cap BF \Rightarrow \) $G$ là trọng tâm của tứ diện $ABCD.$
Giả sử bốn điểm $A, D, G, M$ đồng phẳng.
$A, D, M$\( \in \left( {ACD} \right)\) \( \Rightarrow G \in \left( {ACD} \right) \) \(\Rightarrow AG \subset \left( {ACD} \right)\) \( \Rightarrow E \in \left( {ACD} \right)\)(Vô lí)
Do đó $A, D, M, G $ không đồng phẳng.
Vậy $AD $ và $GM$ là hai đường thẳng chéo nhau.
Cho hình chóp $S.ABC,$ $M $ là một điểm nằm trong tam giác $ABC.$ Các đường thẳng qua $M$ và song song với $SA, SB,SC$ cắt các mặt $(SBC), (SAC), (SAB)$ lần lượt tại $A’, B’, C’.$ \(\dfrac{{MA'}}{{SA}} + \dfrac{{MB'}}{{SB}} + \dfrac{{MC'}}{{SC}}\) có giá trị không đổi bằng bao nhiêu khi $M $ di động trong tam giác $ABC?$
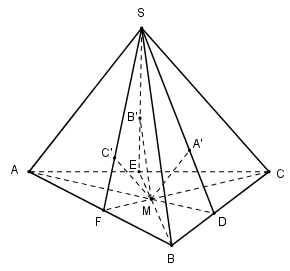
Trong $(SAD) $ ta kẻ đường thẳng qua $M$ và song song với $SA$ cắt $(SBC)$ tại $A’.$
Trong $(SCF)$ kẻ đường thẳng qua $M$ và song song với $SC$ cắt $SF$ tại $C'$
$MA’ // SA$ $ \Rightarrow \dfrac{{MA'}}{{SA}} = \dfrac{{DM}}{{DA}} = \dfrac{{{S_{MBC}}}}{{{S_{ABC}}}}$
Tương tự ta chứng minh được \(\dfrac{{MB'}}{{SB}} = \dfrac{{EM}}{{EB}} = \dfrac{{{S_{MAC}}}}{{{S_{ABC}}}}\) và \(\dfrac{{MC'}}{{SC}} = \dfrac{{FM}}{{FC}} = \dfrac{{{S_{MAB}}}}{{{S_{ABC}}}}\)
Do đó ta có: \(\dfrac{{MA'}}{{SA}} + \dfrac{{MB'}}{{SB}} + \dfrac{{MC'}}{{SC}} = \dfrac{{{S_{MBC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{MAC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{MAB}}}}{{{S_{ABC}}}} = 1\)
Cho tứ diện \(ABCD\) có \(AB = CD = 4,BC = AD = 5,AC = BD = 6\). \(M\) là điểm thay đổi trong tâm giác \(ABC\). Các đường thẳng qua \(M\) song song với \(AD,BD,CD\) tương ứng cắt mặt phẳng \(\left( {BCD} \right),\left( {ACD} \right),\left( {ABD} \right)\) tại \(A',B',C'\). Giá trị lớn nhất của \(MA'.MB'.MC'\) là
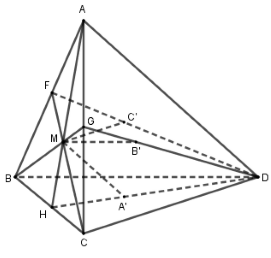
Trong tam giác \(ABC\), kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
+) Trong mặt phẳng \(\left( {HAD} \right)\), kẻ \(MA'//AD\).
+) Trong mặt phẳng \(\left( {GBD} \right)\), kẻ \(MB'//BD\).
+) Trong mặt phẳng \(\left( {FCD} \right)\), kẻ \(MC'//CD\).
Từ đó ta được các điểm \(A',B',C'\) cần tìm.
Theo định lý Ta – let ta có: \(\dfrac{{MA'}}{{AD}} = \dfrac{{HM}}{{HA}} \Rightarrow MA' = 5.\dfrac{{MH}}{{AH}}\)
\(\dfrac{{MB'}}{{BD}} = \dfrac{{GM}}{{GB}} \Rightarrow MB' = 6.\dfrac{{MG}}{{BG}}\); \(\dfrac{{MC'}}{{CD}} = \dfrac{{FM}}{{FC}} \Rightarrow MC' = 4.\dfrac{{MF}}{{CF}}\)
\( \Rightarrow MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}\).
Trong tam giác \(ABC\) ta có: \(1 = \dfrac{{MH}}{{AH}} + \dfrac{{MG}}{{BG}} + \dfrac{{MF}}{{CF}} \ge 3\sqrt[3]{{\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}}}\) \( \Rightarrow \dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le \dfrac{1}{{27}}\)
Do đó \(MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le 120.\dfrac{1}{{27}} = \dfrac{{40}}{9}\)\( \Rightarrow {\left( {MA'.MB'.MC'} \right)_{\max }} = \dfrac{{40}}{9}\)

