Tung một đồng xu không đồng chất $2020$ lần. Biết rằng xác suất xuất hiện mặt sấp là $0,6$. Tính xác suất để mặt sấp xuất hiện đúng $1010$ lần.
Ta có $C_{2020}^{1010}$ cách chọn $1010$ vị trí trong $2020$ lần tung đồng xu để mặt xấp xuất hiện, các lần tung còn lại không xuất hiện mặt sấp. Ứng với mỗi cách chọn cố định 1010 vị trí xuất hiện mặt xấp ta có xác suất của trường hợp đó tính như sau:
+) Tại những lần mặt xấp xuất hiện thì xác suất xảy ra là $0,6$.
+) Tại những lần mặt ngửa xuất hiện thì xác suất xảy ra là $1 - 0,6$.
Do có $1010$ lần xuất hiện mặt sấp và $1010$ xuất hiện mặt ngửa nên ứng với mỗi cách chọn cố định 1010 vị trí xuất hiện mặt xấp thì có xác xuất là ${0,6^{1010}}{\left( {1 - 0,6} \right)^{1010}} = {\left( {0,24} \right)^{1010}}$.
Vậy xác xuất cần tính là $C_{2020}^{1010}.{\left( {0,24} \right)^{1010}}$.
Cho \(5\) chữ số \(1\), \(2\), \(3\), \(4\), \(6\). Lập các số tự nhiên có \(3\) chữ số đôi một khác nhau từ \(5\) chữ số đã cho. Tính tổng của các số lập được.
Nếu chọn chữ số \(1\) làm hàng trăm thì ta có các số sau:
\(123,124,126,134,136,146,\)\(132,142,162,143,163,164\)
Từ đó ta thấy chữ số \(1\) ở hàng trăm xuất hiện \(12\) lần, các chữ số \(2,3,4,6\) ở hàng chục xuất hiện \(3\) lần và ở hàng đơn vị cũng xuất hiện \(3\) lần.
Tổng các số này là: \(12.100 + 3.\left( {20 + 30 + 40 + 60} \right) + 3.\left( {2 + 3 + 4 + 6} \right) = 1695\)
Nếu chọn chữ số \(2\) làm hàng trăm thì ta có tổng là:
\(12.200 + 3.\left( {10 + 30 + 40 + 60} \right) + 3.\left( {1 + 3 + 4 + 6} \right) = 2862\)
Nếu chọn chữ số \(3\) làm hàng trăm thì ta có tổng là:
\(12.300 + 3.\left( {10 + 20 + 40 + 60} \right) + 3.\left( {1 + 2 + 4 + 6} \right) = 4029\)
Nếu chọn chữ số \(4\) làm hàng trăm thì ta có tổng là:
\(12.400 + 3.\left( {10 + 20 + 30 + 60} \right) + 3.\left( {1 + 2 + 3 + 6} \right) = 5196\)
Nếu chọn chữ số \(6\) làm hàng trăm thì ta có tổng là:
\(12.600 + 3.\left( {10 + 20 + 30 + 40} \right) + 3.\left( {1 + 2 + 3 + 4} \right) = 7530\)
Vậy, tổng các số lập được là
\(S = 1695 + 2862 + 4128 + 5196 + 7530\)\( = 21312\).
Cho tập hợp $A = \left\{ {1;2;3;4...;100} \right\}$. Gọi $S$ là tập hợp gồm tất cả các tập con của \(A\), mỗi tập con này gồm 3 phần tử của \(A\) và có tổng bằng \(91.\) Chọn ngẫu nhiên một phần tử của $S.$ Xác suất chọn được phần tử có $3$ số lập thành cấp số nhân bằng?
Giả sử tập con bất kì \(\left\{ {a,b,c} \right\} \in S\)$ \Rightarrow 1 \le a,b,c \le 100$ ;\(a,b,c\) phân biệt.
$a + b + c = 91.$
Số bộ \(a,b,c\) là \(C_{91 - 1}^{3 - 1}\)
Tuy nhiên trong các bộ trên vẫn chứa các bộ có 2 số giống nhau, số bộ có 2 số giống nhau là \(3.45 = 135\) (bộ). ( Không có bộ nào có 3 số giống nhau vì $a + b + c = 91$)
Vậy \(n\left( \Omega \right) = \left( {C_{90}^2 - 3.45} \right):3! = 645\).
Gọi $A$ là biến cố: ”$a,b,c$ lập thành cấp số nhân”
Gọi \(q\) là công bội của cấp số nhân theo bài ra ta có \(q > 0\)
\(a + aq + a{q^2} = 91\)\( \Leftrightarrow a\left( {1 + q + {q^2}} \right) =91 \)
\( \Leftrightarrow {q^2} + q + 1 - \dfrac{{91}}{a} = 0\)
Thử \(a = 1,2,..,91\) và bấm máy tính tìm \(q\) ta được các trường hợp sau:
+) \(a = 1,q = 9\) nên bộ ba số là \(1;9;81\).
+) \(a = 7,q = 3\) nên bộ ba số là \(7;21;63\).
+) \(a = 13,q = 2\) nên bộ ba số là \(13;26;52\).
+) \(a = 25,q = \dfrac{6}{5}\) nên bộ ba số là \(25;30;36\).
Vậy có bốn bộ số thỏa mãn.
\(P\left( A \right) = \dfrac{4}{{645}}\).
Với \(n\) là số nguyên dương thỏa mãn \(C_n^1 + C_n^2 = 55\), hệ số của \({x^5}\) trong khai triển của biểu thức \({\left( {{x^3} + \dfrac{2}{{{x^2}}}} \right)^n}\) bằng
Ta có \(C_n^1 + C_n^2 = 55\)\( \Leftrightarrow n + \dfrac{{n\left( {n - 1} \right)}}{2} = 55\)\( \Leftrightarrow {n^2} + n - 110 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = 10\\n = - 11\end{array} \right.\)\( \Rightarrow n = 10\).
Số hạng tổng quát trong khai triển \({\left( {{x^3} + \dfrac{2}{{{x^2}}}} \right)^{10}}\) là \({T_{k + 1}} = C_{10}^k{\left( {{x^3}} \right)^{10 - k}}.{\left( {\dfrac{2}{{{x^2}}}} \right)^k}\)\( = C_{10}^k{.2^k}.{x^{30 - 5k}}\).
Số hạng chứa \({x^5}\) ứng với \(30 - 5k = 5 \Leftrightarrow k = 5\).
Vậy, hệ số của \({x^5}\) trong khai triển của biểu thức \({\left( {{x^3} + \dfrac{2}{{{x^2}}}} \right)^{10}}\) bằng \(C_{10}^5{.2^5} = 8064\).
Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng \(\overline {abcd} \), trong đó \(1 \le a \le b \le c \le d \le 9\).
Cách 1: Số tự nhiên có bốn chữ số có dạng \(\overline {abcd} \)
\(a \in \left\{ {1;\,2;\,3;\,4;\,5;\,6;\,7;\,8;\,9} \right\}\) suy ra có \(9\) cách chọn
\(\overline {bcd} \) có \({10^3}\) cách chọn
Suy ra số phần tử của không gian mẫu là \(n\left( \Omega \right) = {9.10^3} = 9000\).
Gọi \(A\) là biến cố ‘‘số được chọn có dạng \(\overline {abcd} \), trong đó \(1 \le a \le b \le c \le d \le 9\)’’
Số dạng $\overline {aaaa} $ có \(9\) số.
Số dạng $\overline {abcd} $ (\(a < b < c < d\)) có \(C_9^4\) số.
Số dạng $\overline {aaab} $ có \(C_9^2\) số.
Số dạng $\overline {aabb} $ có \(C_9^2\) số.
Số dạng $\overline {abbb} $ có \(C_9^2\) số.
Số dạng $\overline {aabc} $ có \(C_9^3\) số.
Số dạng $\overline {abbc} $ có \(C_9^3\) số.
Số dạng $\overline {abcc} $ có \(C_9^3\) số.
\(n\left( A \right) = 9 + C_9^4 + 3.C_9^2 + 3.C_9^3 = 495\).
Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{495}}{{9000}} = 0,055\).
Gọi \(S\) là tập hợp tất cả các số tự nhiên có \(7\) chữ số và chia hết cho \(9\). Chọn ngẫu nhiên một số từ tập \(S\), tính xác suất để các chữ số của số đó đôi một khác nhau.
Số chia hết cho \(9\) có dạng: \(9m\), với \(m \in \mathbb{Z}\).
Ta có \(1000000 \le 9m < 10000000\)\( \Leftrightarrow 111111 < m \le 1111111\).
Do đó có \(1000000\) số có \(7\) chữ số và chia hết cho \(9\).
Từ các chữ số \(0;1;2;...;9\) ta có các bộ gồm \(7\) chữ số có tổng chia hết cho \(9\) là
\(\left( {0;2;3;4;5;6;7} \right)\); \(\left( {0;1;3;4;5;6;8} \right)\); \(\left( {0;1;2;4;5;7;8} \right)\); \(\left( {0;1;2;4;5;6;9} \right)\) \(\left( {0;1;2;3;6;7;8} \right)\); \(\left( {0;3;4;5;7;8;9} \right)\);
\(\left( {0;2;4;6;7;8;9} \right)\); \(\left( {0;1;5;6;7;8;9} \right)\); \(\left( {0;1;2;3;4;8;9} \right)\); \(\left( {0;1;2;3;5;7;9} \right)\); \(\left( {2;3;4;5;6;7;9} \right)\);
\(\left( {1;3;4;5;6;8;9} \right)\); \(\left( {1;2;4;5;7;8;9} \right)\); \(\left( {1;2;3;6;7;8;9} \right)\).
Có \(10\) bộ số gồm \(7\) số có tổng chia hết cho \(9\) trong đó có số \(0\) nên từ các bộ số này lập được: \(10 \times 6 \times 6! = 43200\) số có \(7\) chữ số đôi một khác nhau và chia hết cho \(9\).
Có \(4\) bộ số gồm \(7\) số có tổng chia hết cho \(9\) tương tự như bộ số \(\left( {2;3;4;5;6;7;9} \right)\), nên từ các bộ số này lập được \(4 \times 7! = 20160\) số có \(7\) chữ số đôi một khác nhau và chia hết cho \(9\).
Vậy, xác suất chọn một số từ tập \(S\) để được một số có các chữ số của số đó đôi một khác nhau là \(P = \dfrac{{43200 + 20160}}{{1000000}} = \dfrac{{198}}{{3125}}\).
Cho số nguyên dương \(n\) thỏa mãn \(C_{2n}^1 + C_{2n}^3 + \cdots + C_{2n}^{2n - 1} = 512\). Tính tổng \(S = {2^2}C_n^2 - {3^2}C_n^3 + \cdots + {\left( { - 1} \right)^n}.{n^2}.C_n^n\).
Ta có \({\left( {1 + x} \right)^{2n}} = C_{2n}^0 + C_{2n}^1.x + C_{2n}^2.{x^2} + C_{2n}^3.{x^3} + \cdots + C_{2n}^{2n - 1}.{x^{2n - 1}} + C_{2n}^{2n}.{x^{2n}}\)\(\left( 1 \right)\).
Thay \(x = 1\) vào \(\left( 1 \right)\) ta có: \({2^{2n}} = C_{2n}^0 + C_{2n}^1 + C_{2n}^2 + C_{2n}^3 + \cdots + C_{2n}^{2n - 1} + C_{2n}^{2n}\)\(\left( 2 \right)\).
Thay \(x = - 1\) vào \(\left( 1 \right)\) ta có: \(0 = C_{2n}^0 - C_{2n}^1 + C_{2n}^2 - C_{2n}^3 + \cdots - C_{2n}^{2n - 1} + C_{2n}^{2n}\)\(\left( 3 \right)\).
Trừ từng vế của \(\left( 2 \right)\) và \(\left( 3 \right)\) ta có:
\({2^{2n}} = 2.\left( {C_{2n}^1 + C_{2n}^3 + \cdots + C_{2n}^{2n - 1}} \right)\)\( \Leftrightarrow C_{2n}^1 + C_{2n}^3 + \cdots + C_{2n}^{2n - 1} = {2^{2n - 1}}\).
Nên \(C_{2n}^1 + C_{2n}^3 + \cdots + C_{2n}^{2n - 1} = 512\)\( \Leftrightarrow {2^{2n - 1}} = {2^9}\)\( \Leftrightarrow 2n - 1 = 9\)\( \Leftrightarrow n = 5\).
Hay \(S = {2^2}C_5^2 - {3^2}C_5^3 + {4^2}C_5^4 - {5^2}.C_5^5 = 5\).
Trong mặt phẳng tọa độ $Oxy$, cho hình chữ nhật \(OMNP\) với \(M\left( {0;10} \right)\), \(N\left( {100;10} \right)\), \(P\left( {100;0} \right)\) Gọi S là tập hợp tất cả các điểm \(A\left( {x;y} \right)\) với \(x\), \(y \in \mathbb{Z}\) nằm bên trong kể cả trên cạnh của hình chữ nhật \(OMNP\). Lấy ngẫu nhiên 1 điểm \(A\left( {x;y} \right) \in S\). Tính xác suất để \(x + y \le 90\).
Cách 1: Tập hợp \(S\) gồm có \(11.101 = 1111\) điểm.
Ta xét \(S' = \left\{ {\left( {x;y} \right):x + y > 90} \right\}\)với \(0 \le x \le 100\) và \(0 \le y \le 10\)
- Khi \(y = 0\) \( \Rightarrow \)\(x > 90\) \( \Rightarrow \)\(x = \overline {91;100} \) \( \Rightarrow \) có \(10\) giá trị của \(x\)
- Khi \(y = 1\) \( \Rightarrow \)\(x > 89\) \( \Rightarrow \)\(x = \overline {90;100} \) \( \Rightarrow \) có \(11\) giá trị của \(x\)
- Khi \(y = 10\) \( \Rightarrow \)\(x > 90\) \( \Rightarrow \)\(x = \overline {91;100} \) \( \Rightarrow \) có \(20\) giá trị của \(x\)
Như vậy \(S'\) có 165 phần tử. Vậy xác suất cần tìm là \(\dfrac{{1111 - 165}}{{1111}} = \dfrac{{86}}{{101}}\).
Cách 2:
Nhận thấy các điểm cần tìm nằm trên các đường thẳng \(y = m\), \(m = \overline {0;10} \).
Dễ thấy trên các đường thẳng \(y = 0\), \(y = 1\), \(y = 2...\), \(y = 10\) có lần lượt \(91\), \(90\), \(89...\),\(81\) điểm.
Vậy xác suất cần tìm là \(p\left( A \right) = \dfrac{{91 + 90 + ... + 81}}{{11.101}} = \dfrac{{86}}{{101}}\).
Cách 3:
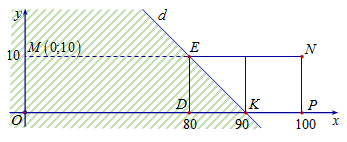
\(n\left( \Omega \right) = 11.101 = 1111\).
Ta thấy $x + y \le 90$ có miền nghiệm là nửa mặt phẳng có bờ là đường thẳng $d$ chứa điểm $O$.
Số điểm thuôc hcn $ENPD$ là $21.11 = 231$
Số điểm thuộc $\Delta EDK$ tính cả cạnh $EK$ là $55 + 11 = 66$
Suy ra $x + y > 90$ có $231 - 66 = 165$ điểm và $x + y \le 90$ có \(1111 - 165 = 946\)
\(P\left( A \right) = \dfrac{{946}}{{1111}} = \dfrac{{86}}{{101}}\)
Có \(12\) người xếp thành một hàng dọc (vị trí của mỗi người trong hàng là cố định), Chọn ngẫu nhiên \(3\) người trong hàng. Tính xác suất để \(3\) người được chọn không có \(2\) người đứng nào cạnh nhau
- Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{12}^3 = 220\).
- Giả sử chọn ba người có số thứ tự trong hàng lần lượt là \(m\), \(n\), \(p\).
Theo giả thiết ta có: \(\left\{ \begin{array}{l}m < n < p\\n - m > 1\\p - n > 1\\m,n,p \in \left\{ {1;2;...;12} \right\}\end{array} \right.\)
- Đặt \(\left\{ \begin{array}{l}a = m\\b = n - 1\\c = p - 2\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a < b < c\\b - a \ge 1\\c - b \ge 1\\1 \le a < b < c = p - 2 \le 10\end{array} \right.\)
\( \Rightarrow a\), \(b\), \(c\) là ba số bất kì trong tập \(\left\{ {1;2;3;...;10} \right\}\)\( \Rightarrow \) có \(C_{10}^3\) cách chọn hay \(n\left( A \right) = C_{10}^3 = 120\).
Vậy xác suất là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{120}}{{220}} = \dfrac{6}{{11}}\).
Có hai học sinh lớp $A,$ ba học sinh lớp \(B\) và bốn học sinh lớp \(C\) xếp thành một hàng ngang sao cho giữa hai học sinh lớp \(A\) không có học sinh nào lớp \(B.\) Hỏi có bao nhiêu cách xếp hàng như vậy?
Xét các trường hợp sau:
TH1: Hai học sinh lớp A đứng cạnh nhau có \(2!.8!\) cách.
TH2: Giữa hai học sinh lớp A có một học sinh lớp C có \(2!.A_4^1.7!\) cách.
TH3: Giữa hai học sinh lớp A có hai học sinh lớp C có \(2!.A_4^2.6!\) cách.
TH4: Giữa hai học sinh lớp A có ba học sinh lớp C có \(2!.A_4^3.5!\) cách.
TH5: Giữa hai học sinh lớp A có bốn học sinh lớp C có \(2!.A_4^4.4!\) cách.
Vậy theo quy tắc cộng có $2!\left( {8! + A_4^17! + A_4^26! + A_4^35! + A_4^44!} \right) = 145152$ cách.
Từ các số $\left\{ {0;\;1;\;2;\;3;\;4;\;5;\;6} \right\}$ viết ngẫu nhiên một số tự nhiên gồm $6$ chữ số khác nhau có dạng $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} $. Tính xác suất để viết được số thoả mãn điều kiện ${a_1} + {a_2} = {a_3} + {a_4} = {a_5} + {a_6}$.
Ta dễ có số phần tử của không gian mẫu là $\left| \Omega \right| = 6.A_6^5 = 4320$.
Gọi $A$ là biến cố “chọn được số thoả mãn yêu cầu bài toán”. Khi đó ta có $3$ phương án để chọn số $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} $ như sau:
- Phương án $1$: ${a_1} + {a_2} = {a_3} + {a_4} = {a_5} + {a_6} = 5$. Khi đó
$\left\{ {\left( {{a_1},{a_2}} \right);\left( {{a_3},{a_4}} \right);\left( {{a_5},{a_6}} \right)} \right\} \subset \left\{ {\left( {0,5} \right);\left( {1,4} \right);\left( {2,3} \right)} \right\}$.
- Phương án $1.1$: $\left( {{a_1},{a_2}} \right) = \left( {0,5} \right) \Rightarrow $có $2.{\left( {2!} \right)^2}$ cách chọn;
- Phương án $1.2$: $\left( {{a_1},{a_2}} \right) \ne \left( {0,5} \right) \Rightarrow $có $4.{\left( {2!} \right)^3}$ cách chọn.
Vậy có $2.{\left( {2!} \right)^2} + 4.{\left( {2!} \right)^3} = 40$ cách chọn.
- Phương án $2$: ${a_1} + {a_2} = {a_3} + {a_4} = {a_5} + {a_6} = 6$. Khi đó
$\left\{ {\left( {{a_1},{a_2}} \right);\left( {{a_3},{a_4}} \right);\left( {{a_5},{a_6}} \right)} \right\} \subset \left\{ {\left( {0,6} \right);\left( {1,5} \right);\left( {2,4} \right)} \right\}$. Phương án này hoàn toàn tương tự phương án $1$ do đó có $2.{\left( {2!} \right)^2} + 4.{\left( {2!} \right)^3} = 40$ cách chọn.
- Phương án $1$: ${a_1} + {a_2} = {a_3} + {a_4} = {a_5} + {a_6} = 7$. Khi đó
$\left\{ {\left( {{a_1},{a_2}} \right);\left( {{a_3},{a_4}} \right);\left( {{a_5},{a_6}} \right)} \right\} \subset \left\{ {\left( {1,6} \right);\left( {2,5} \right);\left( {3,4} \right)} \right\}$, suy ra có $3!.{\left( {2!} \right)^3} = 48$ cách chọn.
Vậy số phần tử của $A$: $\left| A \right| = 40.2 + 48 = 128$. Suy ra $p = \dfrac{{\left| A \right|}}{{\left| \Omega \right|}} = \dfrac{{128}}{{4320}} = \dfrac{4}{{135}}$.
Cho một đa giác lồi $\left( H \right)$ có $30$ đỉnh. Chọn ngẫu nhiên $4$ đỉnh của đa giác đó. Gọi $P$ là xác suất sao cho $4$ đỉnh được chọn tạo thành một tứ giác có bốn cạnh đều là đường chéo của $\left( H \right)$. Hỏi $P$ gần với số nào nhất trong các số sau?
Số phần tử của không gian mẫu là \(n\left( \Omega \right) = C_{30}^4\).
Gọi \(A\): “$4$ đỉnh được chọn tạo thành một tứ giác có bốn cạnh đều là đường chéo của $\left( H \right)$”.
Để chọn ra một tứ giác thỏa mãn đề bài ta làm như sau:
Bước 1: Chọn đỉnh đầu tiên của tứ giác, có $30$ cách.
Bước 2: Chọn $3$ đỉnh còn lại sao cho hai đỉnh bất kỳ của tứ giác cách nhau ít nhất 1 đỉnh. Điều này tương đương với việc ta phải chia $m = 30$ chiếc kẹo cho $n = 4$ đứa trẻ sao cho mỗi đứa trẻ có ít nhất $k = 2$ cái, có \(C_{m - n(k - 1) - 1}^{n - 1} = C_{25}^3\) cách, nhưng làm như thế mỗi tứ giác lặp lại 4 lần.
\( \Rightarrow \) Số phần tử của biến cố \(A\) là \(n\left( A \right) = \dfrac{{30.C_{25}^3}}{4}\).
Vậy xác suất của biến cố \(A\) là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{\dfrac{{30.C_{25}^3}}{4}}}{{C_{30}^4}} = \dfrac{{1150}}{{1827}} \approx 0,6294\).
Giả sử \({\left( {1 + x + {x^2} + {x^3} + ... + {x^{10}}} \right)^{11}} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + ... + {a_{110}}{x^{110}}\) với \({a_0}\), \({a_1}\), \({a_2}\), …, \({a_{110}}\) là các hệ số. Giá trị của tổng \(T = C_{11}^0{a_{11}} - C_{11}^1{a_{10}} + C_{11}^2{a_9} - C_{11}^3{a_8} + ... + C_{11}^{10}{a_1} - C_{11}^{11}{a_0}\) bằng
Ta có: \(A = {\left( {1 + x + {x^2} + {x^3} + ... + {x^{10}}} \right)^{11}} \Leftrightarrow {\left( {1 - x} \right)^{11}}A = {\left( {1 - {x^{11}}} \right)^{11}}\)
\( \Leftrightarrow \underbrace {\sum\limits_{k = 0}^{11} {C_{11}^k} {{\left( { - x} \right)}^k}.\sum\limits_{i = 0}^{110} {{a_i}{x^i}} }_P = \underbrace {\sum\limits_{m = 0}^{11} {C_{11}^m} {{\left( { - {x^{11}}} \right)}^m}}_Q\).
Hệ số của \({x^{11}}\) trong \(P\) là \(C_{11}^0{a_{11}} - C_{11}^1{a_{10}} + C_{11}^2{a_9} - C_{11}^3{a_8} + ... + C_{11}^{10}{a_1} - C_{11}^{11}{a_0} = T\)
Hệ số của \({x^{11}}\) trong \(Q\) là \( - C_{11}^1\)
Vậy \(T = - C_{11}^1 = - 11\).
Cho đa giác đều $2018$ đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn $100^\circ $?
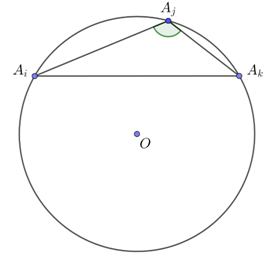
Gọi \({A_1}\),\({A_2}\),…,\({A_{2018}}\) là các đỉnh của đa giác đều \(2018\) đỉnh.
Gọi \(\left( O \right)\) là đường tròn ngoại tiếp đa giác đều \({A_1}{A_2}...{A_{2018}}\).
Các đỉnh của đa giác đều chia \(\left( O \right)\) thành \(2018\) cung tròn bằng nhau, mỗi cung tròn có số đo bằng \(\dfrac{{360^\circ }}{{2018}}\).
Vì tam giác cần đếm có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp của \(\left( O \right)\).
Suy ra góc lớn hơn \(100^\circ \) sẽ chắn cung có số đo lớn hơn \(200^\circ \).
Cố định một đỉnh \({A_i}\). Có \(2018\) cách chọn \({A_i}\).
Gọi \({A_i}\),\({A_j}\),\({A_k}\) là các đỉnh sắp thứ tự theo chiều kim đồng hồ sao cho số đo cung nhỏ \({A_i}{A_k} < 160^\circ \) thì số đo cung lớn \({A_i}{A_k} > 360 - 160^\circ = {200^{\rm{o}}}\) \( \Rightarrow \widehat {{A_i}{A_j}{A_k}} > 100^\circ \) và tam giác \({A_i}{A_j}{A_k}\) là tam giác cần đếm.
Khi đó cung \({A_i}{A_k}\) là hợp liên tiếp của nhiều nhất \(\left[ {\dfrac{{160}}{{\dfrac{{360}}{{2018}}}}} \right] = 896\) cung tròn nói trên.
\(896\) cung tròn này có \(897\) đỉnh. Trừ đi đỉnh \({A_i}\) thì còn \(896\) đỉnh. Do đó có \(C_{896}^2\) cách chọn hai đỉnh \({A_j}\),\({A_k}\).
Vậy có tất cả \(2018.C_{896}^2\) tam giác thỏa mãn yêu cầu bài toán.
Cho khai triển \({\left( {1 + x + {x^2}} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_{2n}}{x^{2n}}\), với \(n \ge 2\) và \({a_0}\), \({a_1}\), \({a_2}\), ..., \({a_{2n}}\) là các hệ số. Biết rằng \(\dfrac{{{a_3}}}{{14}} = \dfrac{{{a_4}}}{{41}}\), khi đó tổng \(S = {a_0} + {a_1} + {a_2} + \ldots + {a_{2n}}\) bằng
Ta có \({\left( {1 + x + {x^2}} \right)^n} = \sum\limits_{k = 0}^n {C_n^k} {\left( {x + {x^2}} \right)^k} = \sum\limits_{k = 0}^n {C_n^k} \sum\limits_{l = 0}^k {C_k^l} {x^{k - l}}.{x^{2l}}\).
Hệ số của \({x^3}\) là \({x^{k + l}} = {x^3} \Rightarrow k + l = 3 \Rightarrow \left[ {\begin{array}{*{20}{c}}{l = 0;\,k = 3}\\{l = 1;\,k = 2}\end{array}} \right. \Rightarrow {a_3} = C_n^3C_3^0 + C_n^2C_2^1\).
Tương tự hệ số của \({x^4}\) là \({x^{k + l}} = {x^4} \Rightarrow k + l = 4 \Rightarrow \left[ {\begin{array}{*{20}{c}}{l = 0;\,k = 4}\\{l = 1;\,k = 3}\\{l = 2;\,k = 2}\end{array}} \right. \Rightarrow {a_4} = C_n^4C_4^0 + C_n^3C_3^1 + C_n^2C_2^2 \).
Theo giả thiết \(14{a_4} = 41{a_3} \Leftrightarrow 14\left( {C_n^4C_4^0 + C_n^3C_3^1 + C_n^2C_2^2} \right) = 41\left( {C_n^3C_3^0 + C_n^2C_2^1} \right)\)
\( \Leftrightarrow 14\left( {\dfrac{{n!}}{{4!\left( {n - 4} \right)!}} + \dfrac{{3.n!}}{{3!\left( {n - 3} \right)!}} + \dfrac{{n!}}{{2!\left( {n - 2} \right)!}}} \right) = 41\left( {\dfrac{{n!}}{{3!\left( {n - 3} \right)!}} + \dfrac{{2.n!}}{{2!\left( {n - 2} \right)!}}} \right)\)
\( \Leftrightarrow 14\left( {\dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)}}{{24}} + \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{2} + \dfrac{{n\left( {n - 1} \right)}}{2}} \right) = 41\left( {\dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{6} + n\left( {n - 1} \right)} \right)\)
\( \Leftrightarrow n\left( {n - 1} \right)\left( {\dfrac{{14}}{{24}}{n^2} - \dfrac{{11}}{4}n - \dfrac{{185}}{6}} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{n = 1}\\{n = 10}\end{array}} \right.\,\,\left( {n \in {\mathbb{N}^ * }} \right)\)
Do \(n \ge 2\) nên \(n = 10\).
Mặt khác thay \(x = 1\) vào hai vế của khai triển \({\left( {1 + x + {x^2}} \right)^{10}} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_{20}}{x^{20}}\) ta được \(S = {a_0} + {a_1} + {a_2} + \ldots + {a_{20}} = {3^{10}}\).
Cho khai triển \({\left( {1 - 3x + 2{x^2}} \right)^{2017}} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_{4034}}{x^{4034}}.\) Tìm \({a_2}.\)
Ta có
\({\left( {1 - 3x + 2{x^2}} \right)^{2017}} = \sum\limits_{k = 0}^{2017} {C_{2017}^k} {\left( {1 - 3x} \right)^k}{\left( {2{x^2}} \right)^{2017 - k}} = \sum\limits_{k = 0}^{2017} {C_{2017}^k} \sum\limits_{i = 0}^k {C_k^i{{\left( { - 3x} \right)}^i}} {\left( {2{x^2}} \right)^{2017 - k}}\)
\(\quad \quad \quad \quad \quad \quad \quad = \sum\limits_{k = 0}^{2017} {\sum\limits_{i = 0}^k {C_{2017}^kC_k^i{{\left( { - 3} \right)}^i}} {{\left( 2 \right)}^{2017 - k}}} {x^{4034 - 2k + i}}\)
Số hạng chứa \({x^2}\) ứng với \(\left\{ \begin{array}{l}4034 - 2k + i = 2\\i,k \in \mathbb{N}\\0 \le k \le 2017,0 \le i \le k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}i = 2k - 4032 \ge 0\\i,k \in \mathbb{N}\\0 \le k \le 2017,0 \le i \le k\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}k = 2016\\i = 0\end{array} \right.\\\left\{ \begin{array}{l}k = 2017\\i = 2\end{array} \right.\end{array} \right.\)
Vậy \({a_2} = C_{2017}^{2016}C_{2016}^0{\left( { - 3} \right)^0}{2^1} + C_{2017}^{2017}C_{2017}^2{\left( { - 3} \right)^2}{2^0} = 18302258\).
Biết rằng trong bóng đá, khi sút phạt, cầu thủ sút phạt ngẫu nhiên vào \(1\) trong bốn vị trí $1$, $2$, $3$, $4$ và thủ môn bay người cản phá ngẫu nhiên đến $1$ trong $4$ vị trí $1$, $2$, $3$, $4$ với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí $1$ (hoặc $2$) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí $3$ (hoặc $4$) thì xác suất cản phá thành công là $50\% $. Tính xác suất của biến cố “cú sút đó không vào lưới”?
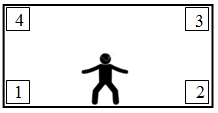
Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 4.4 = 16\)
Gọi biến cố \(A = \) “Cú sút đó không vào lưới”
Khi đó biến cố \(\overline A = \) “Cú sút đó vào lưới”
Trường hợp 1: Cầu thủ sút vào vị trí \(1\) hoặc \(2\).
Cầu thủ có \(2\) cách sút \(\left\{ {1;2} \right\}\)
Thủ môn bay vào vị trí khác vị trí cầu thủ sút có \(3\) cách.
Do đó, có \(2.3 = 6\) khả năng xảy ra.
Xác suất trong TH này là \(\dfrac{6}{{16}} = \dfrac{3}{8}\)
Trường hợp 2: Cầu thủ sút vào vị trí \(3\) hoặc \(4\), thủ môn bay vào \(1\) trong \(3\) vị trí còn lại
Cầu thủ có \(2\) cách sút \(\left\{ {3;4} \right\}\)
Thủ môn bay vào vị trí khác vị trí cầu thủ sút có \(3\) cách.
Do đó, có \(2.3 = 6\) khả năng xảy ra
Xác suất trong TH này là \(\dfrac{6}{{16}} = \dfrac{3}{8}\)
Trường hợp 3: Cầu thủ sút vào vị trí 3 thủ môn bay vào vị trí 3
Cầu thủ có 1 cách sút
Thủ môn có 1 cách bay
Do đó, có 1 khả năng xảy ra.
Xác suất trong TH này là \(\dfrac{1}{{16}}.\dfrac{1}{2} = \dfrac{1}{{32}}\)
Trường hợp 4: Cầu thủ sút vào vị trí 4 thủ môn bay vào vị trí 4
Cầu thủ có 1 cách sút
Thủ môn có 1 cách bay
Do đó, có 1 khả năng xảy ra
Xác suất trong TH này là \(\dfrac{1}{{16}}.\dfrac{1}{2} = \dfrac{1}{{32}}\)
Do đó \(P\left( {\overline A } \right) = \dfrac{3}{8} + \dfrac{3}{8} + \dfrac{1}{{32}} + \dfrac{1}{{32}} = \dfrac{{13}}{{16}}\)
Vậy \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \dfrac{{13}}{{16}} = \dfrac{3}{{16}}\)
Hệ số có giá trị lớn nhất khi khai triển \(P\left( x \right) = {\left( {1 + 2{x^2}} \right)^{12}}\)thành đa thức là
Khai triển: $P\left( x \right) = \sum\limits_{k = 0}^{12} {C_{12}^k{2^k}{x^{2k}}} = \sum\limits_{k = 0}^{12} {{a_k}{x^{2k}}} $ với ${a_k} = C_{12}^k{2^k}$.
${a_{k + 1}} > {a_k}$ \( \Leftrightarrow \) $C_{12}^{k + 1}{2^{k + 1}} > C_{12}^k{2^k}$\( \Leftrightarrow \) $\dfrac{2}{{k + 1}} > \dfrac{1}{{12 - k}} \Leftrightarrow k < \dfrac{{23}}{3} \Leftrightarrow k \le 7$.
Như vậy ${a_0} < {a_1} < {a_2} < ... < {a_8}$.
${a_{k + 1}} < {a_k}$ \( \Leftrightarrow \) $C_{12}^{k + 1}{2^{k + 1}} < C_{12}^k{2^k}$ \( \Leftrightarrow \) $\dfrac{2}{{k + 1}} < \dfrac{1}{{12 - k}} \Leftrightarrow k > \dfrac{{23}}{3} \Leftrightarrow k \ge 8$.
Như vậy ${a_8} > {a_9} > {a_{10}} > ... > {a_{12}}$.
Vậy hệ số có giá trị lớn nhất là ${a_8} = C_{12}^8{2^8} = 126720$.
Gọi $A$ là tập hợp tất cả các số tự nhiên có tám chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc $A$, tính xác suất để số tự nhiên được chọn chia hết cho 45.
Ta có \(n\left( \Omega \right) = A_{10}^8 - A_9^7\).
Gọi $A$ là tập hợp các số \(a\) có 8 chữ số khác nhau chia hết cho \(45\).
Khi đó \(a\) chia hết cho \(5\) và \(9\) (tổng các chữ số chia hết cho \(9\) và số hàng đơn vị bằng \(0\) hoặc \(5\)).
Trường hợp 1: \(a\) có hàng đơn vị bằng \(0\); \(7\) chữ số còn lại có chữ số \(9\) và \(3\) trong \(4\) bộ số \(\left\{ {1;8} \right\}\), \(\left\{ {2;7} \right\}\), \(\left\{ {3;6} \right\}\), \(\left\{ {4;5} \right\}\), có \(4.7!\) số.
Trường hợp 2:\(a\) có hàng đơn vị bằng \(5\); \(7\) chữ số còn lại có chữ số \(4\) và \(3\) trong \(4\) bộ số \(\left\{ {0;9} \right\}\), \(\left\{ {1;8} \right\}\), \(\left\{ {2;7} \right\}\), \(\left\{ {3;6} \right\}\).
* Không có bộ \(\left\{ {0;9} \right\}\), có \(7!\) số.
* Có bộ \(\left\{ {0;9} \right\}\), có \(C_3^2\left( {7! - 6!} \right)\) số
\( \Rightarrow n\left( A \right) = 4.7! + C_3^2\left( {7! - 6!} \right)\) số.
\( \Rightarrow P\left( A \right) = \dfrac{{4.7! + C_3^2\left( {7! - 6!} \right)}}{{A_{10}^8 - A_9^7}} = \dfrac{{53}}{{2268}}\).
Cho 2 bình: bình 1 đựng 6 viên bi xanh và 4 viên bi vàng; bình 2 đựng 3 viên bi xanh và 6 viên bi vàng. An và Bình cùng nhau chơi trò gieo súc sắc như sau: Gieo hai con súc sắc xanh và đỏ. Gọi x, y lần lượt là kết quả số chấm xuất hiện của hai con súc sắc đó. Nếu \(x + y \ge 5\) thì lấy ra 2 viên bi từ bình 1 , còn nếu \(x + y < 5\) thì lấy ra 2 viên bi từ bình 2. Tính xác suất để lấy được ít nhất một viên bi xanh.
(Chỉ được điền các số nguyên vào chỗ trống)
Đáp án:
/
Đáp án:
/
Bước 1: Tính không gian mẫu
Không gian mẫu của phép thử gieo hai con súc sắc xanh và đỏ gồm các bộ số \((x;y)\) thỏa mãn \(x,y \in \{ 1;2; \ldots ;6\} \).
\( \Rightarrow \) Số phần tử của không gian mẫu là \(n(\Omega ) = 6 \times 6 = 36\).
Bước 2: Tính xác suất để \(x + y < 5\) và xác suất để \(x + y \ge 5\)
Ta thấy trong 36 bộ số \((x;y)\) của không gian mẫu chỉ có 6 cặp \((x;y)\) có tổng nhỏ hơn 5 .
Đó là \((1;1),(1;2),(2;1),(1;3),(3;1),(2;2)\).
Vậy xác suất để \(x + y < 5\) là \({P_1} = \dfrac{6}{{36}} = \dfrac{1}{6}\).
Xác suất để \(x + y \ge 5\) là \({P_2} = 1 - \dfrac{1}{6} = \dfrac{5}{6}\).
Bước 3: Tính xác suất lấy được ít nhất 1 viên bi xanh từ bình 1 và xác suất lấy được ít nhất 1 viên bi xanh từ bình 2.
Bình 1 đựng 6 viên bi xanh và 4 viên bi vàng
\( \Rightarrow \) Xác suất lấy cả 2 viên bi vàng từ bình 1 là \(\dfrac{{C_4^2}}{{C_{10}^2}}\)
\( \Rightarrow \) Xác suất lấy được ít nhất 1 viên bi xanh từ bình 1 là \(1 - \dfrac{{C_4^2}}{{C_{10}^2}}\).
Bình 2 đựng 3 viên bi xanh và 6 viên bi vàng
\( \Rightarrow \) Xác suất lấy cả 2 viên bi vàng từ bình 2 là \(\dfrac{{C_6^2}}{{C_9^2}}\)
\( \Rightarrow \) Xác suất lấy được ít nhất 1 viên bi xanh từ bình 2 là \(1 - \dfrac{{C_6^2}}{{C_9^2}}\).
Bước 4: Tính xác suất để lấy được ít nhất 1 bi xanh trong trò chơi
Do đó xác suất để lấy được ít nhất 1 bi xanh trong trò chơi là
\(\dfrac{5}{6}\left( {1 - \dfrac{{C_4^2}}{{C_{10}^2}}} \right) + \dfrac{1}{6}\left( {1 - \dfrac{{C_6^2}}{{C_9^2}}} \right) = \dfrac{{59}}{{72}}\)
