Cho đa giác đều $2018$ đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn $100^\circ $?
Trả lời bởi giáo viên
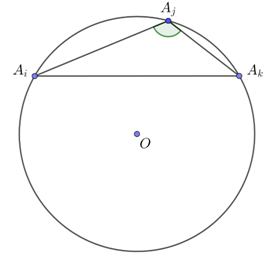
Gọi \({A_1}\),\({A_2}\),…,\({A_{2018}}\) là các đỉnh của đa giác đều \(2018\) đỉnh.
Gọi \(\left( O \right)\) là đường tròn ngoại tiếp đa giác đều \({A_1}{A_2}...{A_{2018}}\).
Các đỉnh của đa giác đều chia \(\left( O \right)\) thành \(2018\) cung tròn bằng nhau, mỗi cung tròn có số đo bằng \(\dfrac{{360^\circ }}{{2018}}\).
Vì tam giác cần đếm có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp của \(\left( O \right)\).
Suy ra góc lớn hơn \(100^\circ \) sẽ chắn cung có số đo lớn hơn \(200^\circ \).
Cố định một đỉnh \({A_i}\). Có \(2018\) cách chọn \({A_i}\).
Gọi \({A_i}\),\({A_j}\),\({A_k}\) là các đỉnh sắp thứ tự theo chiều kim đồng hồ sao cho số đo cung nhỏ \({A_i}{A_k} < 160^\circ \) thì số đo cung lớn \({A_i}{A_k} > 360 - 160^\circ = {200^{\rm{o}}}\) \( \Rightarrow \widehat {{A_i}{A_j}{A_k}} > 100^\circ \) và tam giác \({A_i}{A_j}{A_k}\) là tam giác cần đếm.
Khi đó cung \({A_i}{A_k}\) là hợp liên tiếp của nhiều nhất \(\left[ {\dfrac{{160}}{{\dfrac{{360}}{{2018}}}}} \right] = 896\) cung tròn nói trên.
\(896\) cung tròn này có \(897\) đỉnh. Trừ đi đỉnh \({A_i}\) thì còn \(896\) đỉnh. Do đó có \(C_{896}^2\) cách chọn hai đỉnh \({A_j}\),\({A_k}\).
Vậy có tất cả \(2018.C_{896}^2\) tam giác thỏa mãn yêu cầu bài toán.
Hướng dẫn giải:
- Nhận xét tính chất các đỉnh tạo thành một tam giác có góc lớn hơn $100^0$, từ đó đếm được số các tam giác thỏa mãn.

