Khoảng cách từ một điểm đến một mặt phẳng

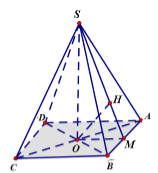
Gọi M là trung điểm của AB, dựng \(OH \bot SM\).

Ta có: \(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\)

Mà \(OH \bot SM \Rightarrow OH \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH\)

Ta có:

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SM \bot AB\\\left( {ABCD} \right) \supset OM \bot AB\end{array} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO = {60^0}\).

\(OM = \dfrac{a}{2},\,\,OH = OM.\sin \angle SMO = OM.\sin {60^0} = \dfrac{a}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}\)

\( \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = \dfrac{{a\sqrt 3 }}{4}\).

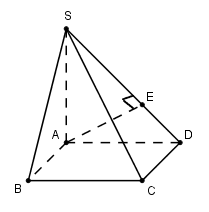
Do AB // CD nên $d\left( {B;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)$.

Kẻ $AE \bot SD$ tại $E$.   (1)

Ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AE\,\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow AE \bot \left( {SCD} \right)\). Khi đó $d\left( {A;\left( {SCD} \right)} \right) = AE.$

Tam giác vuông $SAD,$ có $AE = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{a\sqrt 6 }}{3}.$

Vậy $d\left( {B;\left( {SCD} \right)} \right) = AE = \dfrac{{a\sqrt 6 }}{3}.$

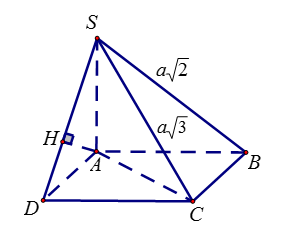
Gọi \(AB = x\), \(\left( {x > 0} \right)\). Xét \(\Delta SAB\) có \(S{A^2} = S{B^2} - A{B^2} = 2{a^2} - {x^2}\).

Xét \(\Delta SAC\) có \(S{C^2} = S{A^2} + A{C^2} \Leftrightarrow 3{a^2} = 2{a^2} - {x^2} + 2{x^2} \Leftrightarrow {x^2} = {a^2} \Leftrightarrow x = a \Rightarrow SA = a\).

Kẻ \(AH \bot SD\), \(\left( {H \in SD} \right)\).

Ta có \(AH \bot \left( {SCD} \right) \Rightarrow d\left( {A\,,\,\left( {SCD} \right)} \right) = AH = \dfrac{{SA.AD}}{{\sqrt[{}]{{S{A^2} + A{D^2}}}}} = \dfrac{a}{{\sqrt[{}]{2}}}\).

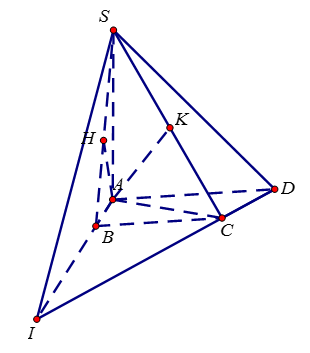
Kẻ \(AH \bot (SBC)\, \Rightarrow AH \bot SB\). Ta có \(d = \dfrac{{HS}}{{BS}}d(B,(SCD)) = \dfrac{{HS}}{{BS}}.\dfrac{{BI}}{{AI}}d(A,(SBC))\)

mà \(\dfrac{{SH}}{{SB}} = \dfrac{{SH.SB}}{{S{B^2}}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{3{a^2}}}{{4{a^2}}} = \dfrac{3}{4}\);

Tam giác \(ADI\)có \(BC\)là đường trung bình nên \(\dfrac{{BI}}{{AI}} = \dfrac{1}{2}\)

Vậy \(d = \dfrac{3}{8}d(A,(SCD)) = \dfrac{3}{8}d\left( {A,SC} \right) = \dfrac{3}{8}\dfrac{{SA.SC}}{{\sqrt {S{A^2} + S{C^2}} }} = \dfrac{3}{8}\dfrac{{a\sqrt 3 .a\sqrt 2 }}{{\sqrt {3{a^2} + 2{a^2}} }} = \dfrac{{3a\sqrt {30} }}{{40}}\)

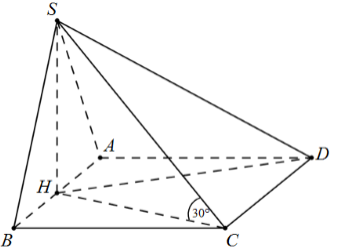
Ta có: $d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right)$$\left( * \right)$.

Trong $\Delta SAC$ : Hạ $HI \bot AC$,ta có :\(HI = \dfrac{{2.{S_{\Delta AHC}}}}{{AC}} = \dfrac{{2.\dfrac{1}{4}.{S_{\Delta ABCD}}}}{{AC}} = \dfrac{{2{a^2}\sqrt 2 }}{{2a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}\) .

Trong $\Delta SHI$: Hạ $HK \bot SI$\( \Rightarrow HK \bot \left( {SAC} \right)\) và \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}}\) \( \Rightarrow HK = \dfrac{{a\sqrt {66} }}{{11}}\).

Vậy $d\left( {B,\left( {SAC} \right)} \right) = 2HK = \dfrac{{2a\sqrt {66} }}{{11}}$.

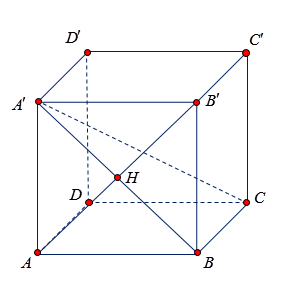
Trong mặt phẳng $\left( {AA'B'B} \right)$, dựng $AH$ vuông góc với $A'B$ tại $H$.

$S$ là hình lập phương nên $BC \bot \left( {AA'B'B} \right)$, suy ra $BC \bot AH$.

Ta có: $\left. \begin{array}{l}AH \bot A'B \subset \left( {A'BC} \right)\\AH \bot BC \subset \left( {A'BC} \right)\end{array} \right\} \Rightarrow AH \bot \left( {A'BC} \right)$ tại $H$.

Do đó: $d\left( {A;(A'BC)} \right) = AH = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{{a\sqrt 2 }}{2}$.

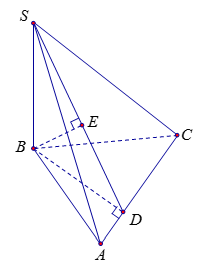
Từ \(B\) kẻ \(BD\) vuông góc \(AC\) tại \(D\), suy ra \(AC \bot \left( {SBD} \right) \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right).\)

Mặt khác \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}}\) nên từ \(B\) kẻ \(BE\) vuông góc \(SD\) tại \(E\) thì \(BE \bot \left( {SAC} \right) \Rightarrow BE = d\left( {B,\,\left( {SAC} \right)} \right).\)

Trong \(\Delta SBD\) vuông tại \(B\), ta có

\(\dfrac{1}{{B{E^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{D^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{A^2}}} + \dfrac{1}{{B{C^2}}}\, = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{16{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{61}}{{144{a^2}}}.\)

Suy ra $BE = \dfrac{{12\sqrt {61} a}}{{61}}\,.$

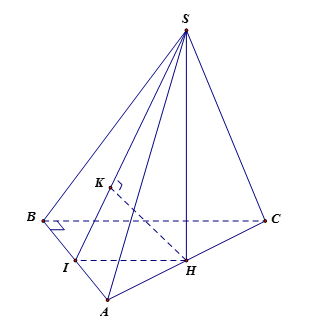
Để tính khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\), ta xác định hình chiếu vuông góc của \(H\) trên mặt phẳng \(\left( {SAB} \right)\) qua các bước sau:

-    Dựng \(HI \bot AB\) với \(I \in AB\), chứng minh được \(AB \bot \left( {SIH} \right)\) và \(\left( {SIH} \right) \bot \left( {SAB} \right) = SI\).

-    Dựng \(K\) là hình chiếu vuông góc của \(H\) trên \(SI\), ta chứng minh được \(SK \bot \left( {SAB} \right)\).

Vậy \(d\left( {H,\left( {SAB} \right)} \right) = HK\).

Do \(HI/{\kern 1pt} /BC\) nên dễ dàng chỉ ra được \(I\) là trung điểm của \(AB\) và \(IH = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 3 }}{2}\), \(IA = IB = \dfrac{{AB}}{2} = \dfrac{a}{2}\).

Ta có \(AB \bot SI\) nên \(SI = \sqrt {S{B^2} - I{B^2}}  = \sqrt {2{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 7 }}{2}\).

Do \(SH \bot IH\) nên xét tam giác vuông \(SIH\) có:

\(SH = \sqrt {S{I^2} - I{H^2}}  = \sqrt {\dfrac{{7{a^2}}}{4} - \dfrac{{3{a^2}}}{4}}  = a\) ; \(HK = \dfrac{{SH.HI}}{{SI}} = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 7 }}{2}}} = \dfrac{{a\sqrt {21} }}{7}\).

Do vậy, ta có \(d\left( {H,\left( {SAB} \right)} \right) = \dfrac{{a\sqrt {21} }}{7}\).

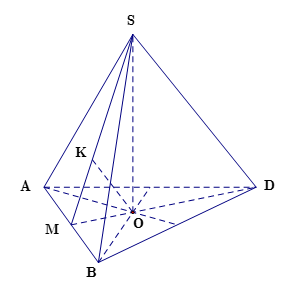
Gọi \(M\) là trung điểm \(AB\), dựng \(OK \bot SM\), ta chứng minh \(OK \bot mp\left( {SAB} \right)\).

Do \(S.ABC\) là hình chóp đều và \(O\) là tâm của đáy \(ABC\) nên \(SO \bot \left( {ABC} \right) \Rightarrow SO \bot AB\).

Do tam giác \(ABC\) đều và \(M\) là trung điểm \(AB\)nên \(AB \bot CM\).

Từ \(SO \bot AB\) và \(AB \bot CM\)suy ra \(AB \bot \left( {SCM} \right) \Rightarrow AB \bot OK\).

Từ \(OK \bot SM\) và \(AB \bot OK\)suy ra \(OK \bot mp\left( {SAB} \right)\). Bởi vậy \(d\left( {O;\left( {SAB} \right)} \right) = OK\).

Ta có \(OM = \dfrac{1}{3}CM = \dfrac{1}{3}.\dfrac{{\left( {2a} \right)\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).

Trong tam giác \(SOM\) vuông tại \(O\) ta có:

\(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}} + \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \dfrac{{10}}{{3{a^2}}} \Rightarrow OK = a\sqrt {\dfrac{3}{{10}}} \).

Vậy \(d\left( {O;\left( {SAB} \right)} \right) = a\sqrt {\dfrac{3}{{10}}} \).

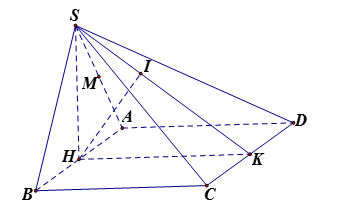
* Gọi $H$ là trung điểm của $AB$ và $K$ là trung điểm của $CD$. Ta có $SH \bot \left( {ABCD} \right)$ và $SH = \dfrac{{a\sqrt 3 }}{2}$. Hạ $HI \bot SK$.

* Khi đó $d\left( {M;\left( {SCD} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SCD} \right)} \right) = \dfrac{1}{2}d\left( {H;\left( {SCD} \right)} \right) = \dfrac{1}{2}HI$.

* Lại có $\dfrac{1}{{H{I^2}}} = \dfrac{1}{{H{S^2}}} + \dfrac{1}{{H{K^2}}} = \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{7}{{3{a^2}}}$.

* Suy ra $HI = \dfrac{{a\sqrt 3 }}{{\sqrt 7 }}$. Vậy $d\left( {M;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt {21} }}{{14}}$.

* Ta có: \(\dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \dfrac{{BD}}{{OD}} = 2\) \( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = 2.d\left( {O;\left( {SCD} \right)} \right) = 2OH\).

Trong đó $H$ là hình chiếu vuông góc của $O$ lên \(\left( {SCD} \right)\).

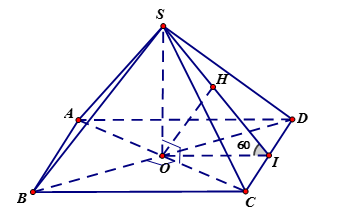
* Gọi $I$ là trung điểm của $CD$ ta có:

$\left\{ \begin{array}{l}SI \bot CD\\OI \bot CD\end{array} \right. \Rightarrow \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \left( {OI;SI} \right) = \widehat {SIO} = 60^\circ $.

Xét tam giác \(SOI\) vuông tại \(O\) ta có: \(SO = OI.\tan 60 = \dfrac{{a\sqrt 3 }}{2}\).

* Do \(SOCD\) là tứ diện vuông tại \(O\) nên:

\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}} + \dfrac{1}{{O{S^2}}} = \dfrac{2}{{{a^2}}} + \dfrac{2}{{{a^2}}} + \dfrac{4}{{3{a^2}}} = \dfrac{{16}}{{3{a^2}}}\)

\( \Rightarrow OH = \dfrac{{a\sqrt 3 }}{4} \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 3 }}{2}\).

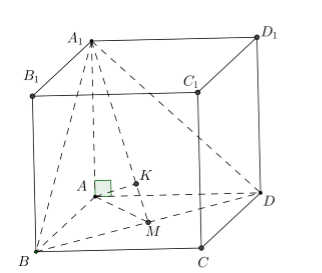
Trong tam giác \(ABD\) kẻ $AM \bot BD$ suy ra $\dfrac{1}{{A{M^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}}$.

.Trong tam giác \({A_1}AM\) kẻ $AK \bot {A_1}M$$ \Rightarrow \dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{A_1}^2}} + \dfrac{1}{{A{M^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} + \dfrac{1}{{9{a^2}}}$$ \Rightarrow AK = \dfrac{6}{7}a$.

Khi đó $AK \bot \left( {{A_1}BD} \right)$ hay $d\left( {A;\left( {{A_1}BD} \right)} \right) = AK = \dfrac{6}{7}a$.

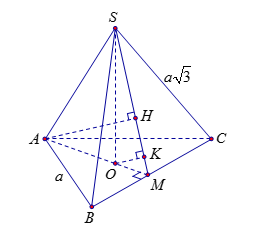
Do tam giác \(ABC\) đều tâm \(O\) suy ra \(AO \bot BC\) tại \(M\) là trung điểm của\(BC\).

Ta có:\(AM = \dfrac{{a\sqrt 3 }}{2},\,MO = \dfrac{1}{3}AM = \dfrac{{a\sqrt 3 }}{6},\,OA = \dfrac{2}{3}AM = \dfrac{{a\sqrt 3 }}{3}\).

Từ giả thiết hình chóp đều suy ra \(SO \bot \left( {ABC} \right)\), \(SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {3{a^2} - \dfrac{{3{a^2}}}{9}}  = \dfrac{{2a\sqrt 6 }}{3}\).

Dựng \(OK \bot SM,AH \bot SM \Rightarrow AH{\rm{//}}OK;\,\,\dfrac{{OK}}{{AH}} = \dfrac{{OM}}{{AM}} = \dfrac{1}{3}\).

Có \(\left\{ \begin{array}{l}BC \bot SO\\BC \bot AM\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot OK\).

Có \(\left\{ \begin{array}{l}OK \bot SM\\OK \bot BC\end{array} \right. \Rightarrow OK \bot \left( {SBC} \right),\,AH \bot \left( {SBC} \right)\,\,\left( {{\rm{ do }}AH{\rm{//}}OK} \right)\).

Từ đó có \({d_1} = d\left( {A,\left( {SBC} \right)} \right) = AH = 3OK;\,{d_2} = d\left( {O,\left( {SBC} \right)} \right) = OK\).

Trong tam giác vuông $OSM$ có đường cao \(OK\) nên:

\(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{{36}}{{3{a^2}}} + \dfrac{9}{{24{a^2}}} = \dfrac{{99}}{{8{a^2}}} \Rightarrow OK = \dfrac{{2a\sqrt 2 }}{{33}}\).

Vậy \(d = {d_1} + {d_2} = 4OK = \dfrac{{8a\sqrt 2 }}{{33}}\).

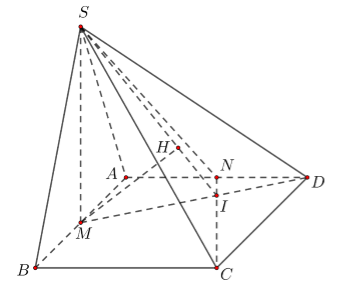
\(M\) là trung điểm của \(AB\) thì \(SM \bot \left( {ABCD} \right)\). Ta có \(SM = \dfrac{{a\sqrt 3 }}{2}\).

Gọi \(I\) là giao điểm của \(NC\) và \(MD\). Ta có \(d\left( {D;\left( {SCN} \right)} \right) = \dfrac{{ID}}{{IM}}d\left( {M;\left( {SCN} \right)} \right)\).

Vì \(ABCD\) là hình vuông nên \(NC \bot DM\) tại \(I\). \(ID.CN = DN.DC\) \( \Leftrightarrow ID = \dfrac{{DN.DC}}{{CN}} = \dfrac{{\dfrac{a}{2}.a}}{{\dfrac{{a\sqrt 5 }}{2}}} = \dfrac{{a\sqrt 5 }}{5}\) \( \Rightarrow IM = DM - ID = \dfrac{{a\sqrt 5 }}{2} - \dfrac{{a\sqrt 5 }}{5} = \dfrac{{3a\sqrt 5 }}{{10}}\) \( \Rightarrow \dfrac{{ID}}{{IM}} = \dfrac{2}{3}\).

Do \(\left\{ \begin{array}{l}IM \bot CN\\CN \bot SM\end{array} \right.\) \( \Rightarrow CN \bot \left( {SMI} \right)\). Kẻ \(MH \bot SI\), vì \(CN \bot MH\) nên \(MH \bot \left( {SCN} \right)\) \( \Rightarrow MH = d\left( {M;\left( {SCN} \right)} \right)\).

Trong tam giác \(SMI\) có \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{M{I^2}}}\) \( = \dfrac{4}{{3{a^2}}} + \dfrac{{20}}{{9{a^2}}} = \dfrac{{32}}{{9{a^2}}}\).

Vậy \(MH = \dfrac{{3a\sqrt 2 }}{8}\)\( \Rightarrow d\left( {D;\left( {SCN} \right)} \right) = \dfrac{{a\sqrt 2 }}{4}\).

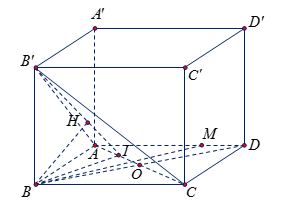
Ta có \(B'C\;{\rm{//}}\;A'D\)\( \Rightarrow B'C\;{\rm{//}}\;\,\left( {ADD'A'} \right) \subset AD'\)\( \Rightarrow d\left( {B'C,AD'} \right)\)\( = d\left( {C,\left( {ADD'A'} \right)} \right)\)\( = CD = a\).

Suy ra  \(x = a\).

Lại có: \(\dfrac{{MA}}{{DA}} = \dfrac{3}{4}\)\( \Rightarrow d\left( {M,\left( {AB'C} \right)} \right)\)\( = \dfrac{3}{4}d\left( {D,\left( {AB'C} \right)} \right)\)\( = \dfrac{3}{4}d\left( {B;\left( {AB'C} \right)} \right)\).

Gọi \(I\) là hình chiếu vuông góc của \(B\) lên \(AC\) ta có: \(\left\{ \begin{array}{l}AC \bot BI\\AC \bot BB'\end{array} \right.\)\( \Rightarrow AC \bot \left( {BB'I} \right)\).

Gọi \(H\) là hình chiếu của \(B\) lên \(B'I\) ta có:

\(\left\{ \begin{array}{l}BH \bot B'I\\BH \bot AC\end{array} \right.\)\( \Rightarrow BH \bot \left( {B'AC} \right)\)\( \Rightarrow d\left( {B,\left( {AB'C} \right)} \right) = BH\).

Trong tam giác \(ABC\), ta có: \(AB.BC = AC.BI\)\( \Rightarrow BI = \dfrac{{AB.BC}}{{AC}} = \dfrac{{a.2a}}{{a\sqrt 5 }} = \dfrac{{2a\sqrt 5 }}{5}\).

Trong tam giác \(BB'I\), ta có: \(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{I^2}}} + \dfrac{1}{{B{{B'}^2}}}\) \( \Rightarrow BH = \dfrac{{BI.BB'}}{{\sqrt {B{I^2} + B{{B'}^2}} }} = \dfrac{{2a}}{3}\)

\( \Rightarrow d\left( {B,\left( {AB'C} \right)} \right) = \dfrac{3}{4}.\dfrac{{2a}}{3} = \dfrac{a}{2}\). Suy ra \(y = \dfrac{a}{2}\)

Vậy \(x.y = \dfrac{{{a^2}}}{2}\).

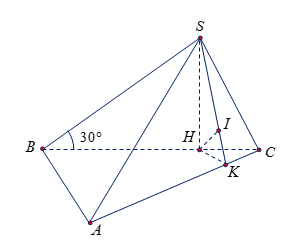
Trong \(\left( {SBC} \right)\), kẻ \(SH \bot BC\) tại $H$. Ta có  nên \(SH \bot \left( {ABC} \right)\).

Ta có \(\Delta SBH\) vuông tại \(H\) có \(SH = SB.\sin 30^\circ  = a\sqrt 3 \); \(BH = SB.\cos 30^\circ  = 3a\);

\(HC = BC - BH = a\).

Khi đó \(BH = 4HC\) nên \(d\left( {B,\,\left( {SAC} \right)} \right) = 4d\left( {H,\,\left( {SAC} \right)} \right)\)

Trong \(\left( {ABC} \right)\), kẻ \(HK \bot AC\); trong \(\left( {SHK} \right)\), kẻ \(HI \bot SK\).

Ta có \(SH \bot AC\) nên \(AC \bot \left( {SHK} \right)\) suy ra \(AC \bot HI\) hay \(HI = d\left( {H,\,\left( {SAC} \right)} \right)\).

 nên \(\dfrac{{HK}}{{AB}} = \dfrac{{CH}}{{CA}}\)\( \Rightarrow HK = \dfrac{{CH.AB}}{{\sqrt {A{B^2} + B{C^2}} }} = \dfrac{{3a}}{5}\).

Tam giác \(SHK\) vuông tại \(H\) có \(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{K^2}}}\)\( \Rightarrow HI = \dfrac{{SH.HK}}{{\sqrt {S{H^2} + H{K^2}} }} = \dfrac{{3\sqrt 7 a}}{{14}}\).

Vậy \(d\left( {B,\,\left( {SAC} \right)} \right) = \dfrac{{6\sqrt 7 a}}{7}\).

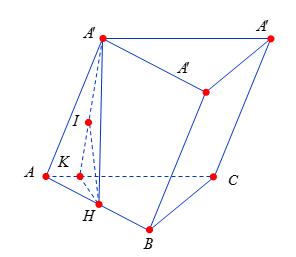
Ta có: $\widehat {A'AH} = 60^\circ  \Rightarrow A'H = AH.\tan 60^\circ  = a\sqrt 3 $.

Kẻ$HK \bot AC,HI \bot A'K \Rightarrow HK = AH.\sin 60^\circ  = \dfrac{{a\sqrt 3 }}{2}$ (hình vẽ).

Ta có $\dfrac{1}{{I{H^2}}} = \dfrac{1}{{H{{A'}^2}}} + \dfrac{1}{{H{K^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{4}{{3{a^2}}} \Rightarrow IH = \dfrac{{\sqrt {15} a}}{5}$.

$d\left( {B,\left( {ACC'A'} \right)} \right) = 2d\left( {H,ACC'A'} \right) = 2HI = \dfrac{{2\sqrt {15} a}}{5}$.

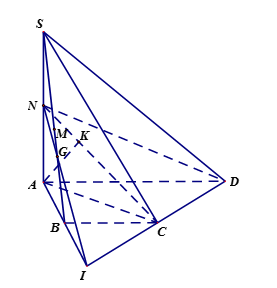
Gọi \(I\) là giao điểm của \(AB\) và \(CD\), vì \(AD = 2BC\) nên \(B\) là trung điểm của \(AI\). Gọi \(G\) là giao điểm của \(SB\) và \(IN\), dễ thấy \(G\) là trọng tâm tam giác \(SAI\). Do đó, \(SG = \dfrac{2}{3}SB = \dfrac{4}{3}SM \Rightarrow MG = \dfrac{1}{4}SG\), mà \(G \in \left( {NCD} \right)\) nên $d\left( {M;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}d\left( {S;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}d\left( {A;\,\left( {NCD} \right)} \right)$.

Lại có, \(CD \bot AC;\,CD \bot SA \Rightarrow CD \bot \left( {SAC} \right)\).

Gọi \(K\) là hình chiếu của \(A\) lên \(NC\) thì $d\left( {A;\,\left( {NCD} \right)} \right) = AK = \dfrac{{AN.AC}}{{\sqrt {A{N^2} + A{C^2}} }}\,\,\,\left( * \right)$, với \(AN = \dfrac{{a\sqrt 3 }}{2};\,AC = a\sqrt 2 \) thay vào \(\left( * \right)\) ta được $AK = \dfrac{{a\sqrt {66} }}{{11}}$. Vậy $d\left( {M;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}AK = \dfrac{{a\sqrt {66} }}{{44}}$

Nhận thấy \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\,\,\left( {do\,\,SA \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAC} \right)\).

\( \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = BC\).

Mà \(\Delta ABC\) là tam giác vuông cân tại \(C\) \( \Rightarrow BC = AC = a\).

\( \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = a\).

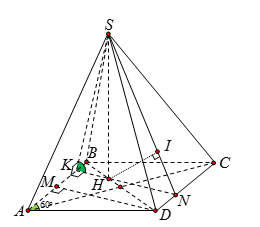
Gọi \(H\) là trọng tâm tam giác \(ABC\), \(M\) là trung điểm \(AB\)

Ta có tam giác \(ABD\) là tam giác đều\( \Rightarrow DM = \dfrac{{a\sqrt 3 }}{2}\) và \(BD = a\)

Kẻ \(HK \bot AB\) \( \Rightarrow HK\,{\rm{//}}\,DM\) \( \Rightarrow \dfrac{{HK}}{{DM}} = \dfrac{{BH}}{{BD}}\) \( \Rightarrow HK = DM.\dfrac{{BH}}{{BD}} = \dfrac{1}{3}DM = \dfrac{{a\sqrt 3 }}{6}\)

\(\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\), \(AB \bot HK\), \(AB \bot SK\) (định lí ba đường vuông góc)

\( \Rightarrow \left( {\widehat {\left( {SAB} \right),\,\left( {ABCD} \right)}} \right) = \widehat {SKH}\)

Tam giác \(SHK\) vuông tại \(H\) có \(SH = HK.\tan 60^\circ  = \dfrac{a}{2}\).

Gọi \(N\) là giao điểm của \(HK\) và \(CD\)

Ta có \(\left\{ \begin{array}{l}HN \bot CD\\SH \bot CD\end{array} \right. \Rightarrow CD \bot \left( {SHN} \right)\); \(CD \subset \left( {SCD} \right)\) \( \Rightarrow \left( {SCD} \right) \bot \left( {SHN} \right)\) và \(\left( {SHN} \right) \cap \left( {SCD} \right) = SN\)

Trong mặt phẳng \(\left( {SHN} \right)\) kẻ \(HI \bot SN\) thì \(HI \bot \left( {SCD} \right)\) \( \Rightarrow HI = d\left( {H,\,\left( {SCD} \right)} \right)\)

Tam giác \(SHN\) vuông tại \(H\) có \(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{N^2}}}\), với \(HN = \dfrac{2}{3}DM = \dfrac{a}{{\sqrt 3 }}\)

\( \Rightarrow HI = \dfrac{{a\sqrt 7 }}{7}\)

Lại có \(\dfrac{{BD}}{{HD}} = \dfrac{3}{2}\) $ \Rightarrow d\left( {B,\,\left( {SCD} \right)} \right) = \dfrac{3}{2}d\left( {H,\,\left( {SCD} \right)} \right)$

Vậy \(d\left( {B,\,\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 7 }}{{14}}\).