Câu hỏi:
2 năm trước
Cho hình chóp tam giác đều \(S.ABC\) có độ dài cạnh đáy bằng \(a\), cạnh bên bằng $a\sqrt 3 $. Gọi \(O\) là tâm của đáy \(ABC\), \({d_1}\) là khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) và \({d_2}\) là khoảng cách từ \(O\) đến mặt phẳng \(\left( {SBC} \right)\). Tính \(d = {d_1} + {d_2}\).
Trả lời bởi giáo viên
Đáp án đúng: c
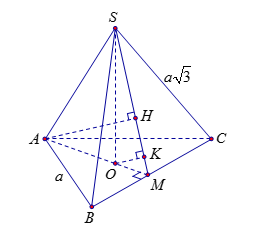
Do tam giác \(ABC\) đều tâm \(O\) suy ra \(AO \bot BC\) tại \(M\) là trung điểm của\(BC\).
Ta có:\(AM = \dfrac{{a\sqrt 3 }}{2},\,MO = \dfrac{1}{3}AM = \dfrac{{a\sqrt 3 }}{6},\,OA = \dfrac{2}{3}AM = \dfrac{{a\sqrt 3 }}{3}\).
Từ giả thiết hình chóp đều suy ra \(SO \bot \left( {ABC} \right)\), \(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {3{a^2} - \dfrac{{3{a^2}}}{9}} = \dfrac{{2a\sqrt 6 }}{3}\).
Dựng \(OK \bot SM,AH \bot SM \Rightarrow AH{\rm{//}}OK;\,\,\dfrac{{OK}}{{AH}} = \dfrac{{OM}}{{AM}} = \dfrac{1}{3}\).
Có \(\left\{ \begin{array}{l}BC \bot SO\\BC \bot AM\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot OK\).
Có \(\left\{ \begin{array}{l}OK \bot SM\\OK \bot BC\end{array} \right. \Rightarrow OK \bot \left( {SBC} \right),\,AH \bot \left( {SBC} \right)\,\,\left( {{\rm{ do }}AH{\rm{//}}OK} \right)\).
Từ đó có \({d_1} = d\left( {A,\left( {SBC} \right)} \right) = AH = 3OK;\,{d_2} = d\left( {O,\left( {SBC} \right)} \right) = OK\).
Trong tam giác vuông $OSM$ có đường cao \(OK\) nên:
\(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{{36}}{{3{a^2}}} + \dfrac{9}{{24{a^2}}} = \dfrac{{99}}{{8{a^2}}} \Rightarrow OK = \dfrac{{2a\sqrt 2 }}{{33}}\).
Vậy \(d = {d_1} + {d_2} = 4OK = \dfrac{{8a\sqrt 2 }}{{33}}\).
Hướng dẫn giải:
Tính các khoảng cách \({d_1},{d_2}\) bằng cách dựng các đoạn vuông góc từ điểm đến mặt phẳng và sử dụng kiến thức hình học đã có để tính toán.
