Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại\(A\)và\(B,\,AB = BC = a,\,AD = 2a.\) Biết \(SA = \sqrt 3 a\) và \(SA \bot (ABCD)\). Gọi \(H\) là hình chiếu vuông góc của \(A\) trên \((SBC).\) Tính khoảng cách $d$ từ \(H\) đến mặt phẳng \((SCD).\)
Trả lời bởi giáo viên
Đáp án đúng: b
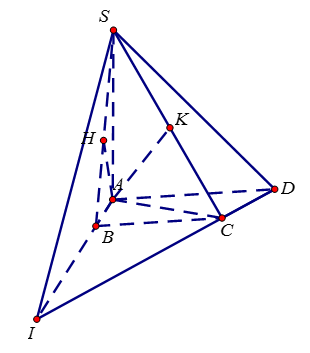
Kẻ \(AH \bot (SBC)\, \Rightarrow AH \bot SB\). Ta có \(d = \dfrac{{HS}}{{BS}}d(B,(SCD)) = \dfrac{{HS}}{{BS}}.\dfrac{{BI}}{{AI}}d(A,(SBC))\)
mà \(\dfrac{{SH}}{{SB}} = \dfrac{{SH.SB}}{{S{B^2}}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{3{a^2}}}{{4{a^2}}} = \dfrac{3}{4}\);
Tam giác \(ADI\)có \(BC\)là đường trung bình nên \(\dfrac{{BI}}{{AI}} = \dfrac{1}{2}\)
Vậy \(d = \dfrac{3}{8}d(A,(SCD)) = \dfrac{3}{8}d\left( {A,SC} \right) = \dfrac{3}{8}\dfrac{{SA.SC}}{{\sqrt {S{A^2} + S{C^2}} }} = \dfrac{3}{8}\dfrac{{a\sqrt 3 .a\sqrt 2 }}{{\sqrt {3{a^2} + 2{a^2}} }} = \dfrac{{3a\sqrt {30} }}{{40}}\)
Hướng dẫn giải:
- Dựng đoạn vuông góc kẻ từ \(H\) đến mặt phẳng \(\left( {SCD} \right)\).
- Sử dụng kiến thức hình học đã biết để tính toán.
