Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\) và cạnh bên \(SB\) vuông góc với mặt phẳng đáy. Cho biết \(SB = 3a\), \(AB = 4a\), \(BC = 2a\). Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right).\)
Trả lời bởi giáo viên
Đáp án đúng: a
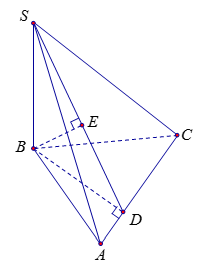
Từ \(B\) kẻ \(BD\) vuông góc \(AC\) tại \(D\), suy ra \(AC \bot \left( {SBD} \right) \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right).\)
Mặt khác \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}}\) nên từ \(B\) kẻ \(BE\) vuông góc \(SD\) tại \(E\) thì \(BE \bot \left( {SAC} \right) \Rightarrow BE = d\left( {B,\,\left( {SAC} \right)} \right).\)
Trong \(\Delta SBD\) vuông tại \(B\), ta có
\(\dfrac{1}{{B{E^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{D^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{A^2}}} + \dfrac{1}{{B{C^2}}}\, = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{16{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{61}}{{144{a^2}}}.\)
Suy ra $BE = \dfrac{{12\sqrt {61} a}}{{61}}\,.$
Hướng dẫn giải:
- Dựng đoạn vuông góc kẻ từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
- Tính toán bằng cách sử dụng kiến thức hình học đã biết.
