Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(\dfrac{{SB}}{{\sqrt[{}]{2}}} = \dfrac{{SC}}{{\sqrt[{}]{3}}} = a\). Cạnh \(SA \bot \left( {ABCD} \right)\), khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
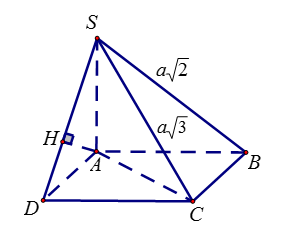
Gọi \(AB = x\), \(\left( {x > 0} \right)\). Xét \(\Delta SAB\) có \(S{A^2} = S{B^2} - A{B^2} = 2{a^2} - {x^2}\).
Xét \(\Delta SAC\) có \(S{C^2} = S{A^2} + A{C^2} \Leftrightarrow 3{a^2} = 2{a^2} - {x^2} + 2{x^2} \Leftrightarrow {x^2} = {a^2} \Leftrightarrow x = a \Rightarrow SA = a\).
Kẻ \(AH \bot SD\), \(\left( {H \in SD} \right)\).
Ta có \(AH \bot \left( {SCD} \right) \Rightarrow d\left( {A\,,\,\left( {SCD} \right)} \right) = AH = \dfrac{{SA.AD}}{{\sqrt[{}]{{S{A^2} + A{D^2}}}}} = \dfrac{a}{{\sqrt[{}]{2}}}\).
Hướng dẫn giải:
Dựng hình chiếu của A lên (SCD), từ đó tính khoảng cách bằng kiến thức hình học đã biết.
