Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật. Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\). Biết \(SD = 2a\sqrt 3 \) và góc tạo bởi đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(30^\circ \). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: b
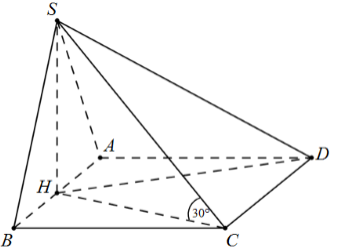
Ta có: $d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right)$$\left( * \right)$.
Trong $\Delta SAC$ : Hạ $HI \bot AC$,ta có :\(HI = \dfrac{{2.{S_{\Delta AHC}}}}{{AC}} = \dfrac{{2.\dfrac{1}{4}.{S_{\Delta ABCD}}}}{{AC}} = \dfrac{{2{a^2}\sqrt 2 }}{{2a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}\) .
Trong $\Delta SHI$: Hạ $HK \bot SI$\( \Rightarrow HK \bot \left( {SAC} \right)\) và \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}}\) \( \Rightarrow HK = \dfrac{{a\sqrt {66} }}{{11}}\).
Vậy $d\left( {B,\left( {SAC} \right)} \right) = 2HK = \dfrac{{2a\sqrt {66} }}{{11}}$.
Hướng dẫn giải:
- Xác định góc \({30^0}\) (góc giữa đường thẳng và mặt phẳng khác \({90^0}\) bằng góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng).
- Sử dụng mối quan hệ khoảng cách từ các điểm thẳng hàng đến cùng một mặt phẳng và tính toán.
