Cho hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có ba kích thước \(AB = a,AD = 2a,A{A_1} = 3a\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {{A_1}BD} \right)\) bằng bao nhiêu?
Trả lời bởi giáo viên
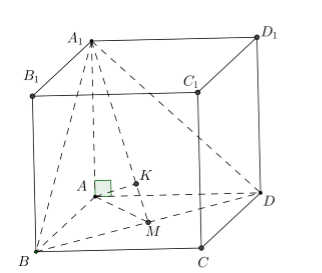
Trong tam giác \(ABD\) kẻ $AM \bot BD$ suy ra $\dfrac{1}{{A{M^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}}$.
.Trong tam giác \({A_1}AM\) kẻ $AK \bot {A_1}M$$ \Rightarrow \dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{A_1}^2}} + \dfrac{1}{{A{M^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} + \dfrac{1}{{9{a^2}}}$$ \Rightarrow AK = \dfrac{6}{7}a$.
Khi đó $AK \bot \left( {{A_1}BD} \right)$ hay $d\left( {A;\left( {{A_1}BD} \right)} \right) = AK = \dfrac{6}{7}a$.
Hướng dẫn giải:
- Dựng đoạn vuông góc kẻ từ \(A\) đến mặt phẳng \(\left( {{A_1}BD} \right)\).
- Tính khoảng cách dựa vào kiến thức hình học đã biết.

