Câu hỏi:
2 năm trước
Cho hình chóp đều \(S.ABCD\), cạnh đáy bằng \(a\), góc giữa mặt bên và mặt đáy là \(60^\circ \). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: c
* Ta có: \(\dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \dfrac{{BD}}{{OD}} = 2\) \( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = 2.d\left( {O;\left( {SCD} \right)} \right) = 2OH\).
Trong đó $H$ là hình chiếu vuông góc của $O$ lên \(\left( {SCD} \right)\).
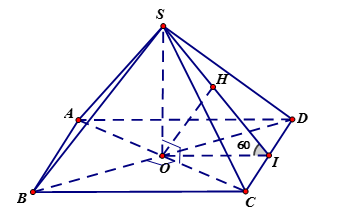
* Gọi $I$ là trung điểm của $CD$ ta có:
$\left\{ \begin{array}{l}SI \bot CD\\OI \bot CD\end{array} \right. \Rightarrow \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \left( {OI;SI} \right) = \widehat {SIO} = 60^\circ $.
Xét tam giác \(SOI\) vuông tại \(O\) ta có: \(SO = OI.\tan 60 = \dfrac{{a\sqrt 3 }}{2}\).
* Do \(SOCD\) là tứ diện vuông tại \(O\) nên:
\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}} + \dfrac{1}{{O{S^2}}} = \dfrac{2}{{{a^2}}} + \dfrac{2}{{{a^2}}} + \dfrac{4}{{3{a^2}}} = \dfrac{{16}}{{3{a^2}}}\)
\( \Rightarrow OH = \dfrac{{a\sqrt 3 }}{4} \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 3 }}{2}\).
Hướng dẫn giải:
- Sử dụng mối quan hệ khoảng cách từ các điểm đến đường thẳng \(d\left( {B;\left( {SCD} \right)} \right) = 2.d\left( {O;\left( {SCD} \right)} \right)\).
- Dựng đoạn vuông góc kẻ từ \(O\) đến \(\left( {SCD} \right)\) và tính toán dựa trên kiến thức hình học đã biết.
